Bài 41 trang 175 SGK Toán 12 nâng cao
Hướng dẫn giải:
Câu a:
Câu b:
Câu c:
Đặt
Câu d:
Đặt
Do đó:
Bài 42 trang 175 SGK Toán 12 nâng cao
Hướng dẫn giải:
Câu a:
Đặt
Do đó:
Câu b:
Đặt
Câu c:
Đặt
Câu d:
Đặt
Đặt
Từ (1) suy ra:
Bài 43 trang 176 SGK Toán 12 nâng cao
Tìm nguyên hàm của các hàm số sau:
a. y = x.e-x
b.
Hướng dẫn giải:
Câu a:
Đặt
Câu b:
Đặt
Do đó:
Bài 44 trang 176 SGK Toán 12 nâng cao
Tìm hàm số y = f(x) nếu biết dy = 12x(3x2 − 1)3dx và f(1) = 3
Hướng dẫn giải:
Ta có:
Đặt
Do đó:
Vì f(1) = 3 nên
Vậy
Bài 45 trang 176 SGK Toán 12 nâng cao
Xác định số b dương để tích phân
Hướng dẫn giải:
Ta có:
Xét hàm số
Ta có:
Bảng biến thiên
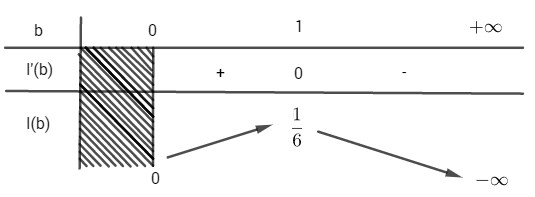
I(b) đạt giá trị lớn nhất bằng 1/6 khi b = 1
Bài 46 trang 176 SGK Toán 12 nâng cao
Cho biết
Hãy tìm:
Hướng dẫn giải:
Câu a:
Câu b:
Câu c:
Câu d:
Bài 47 trang 176 SGK Toán 12 nâng cao
Cho hàm số f liên tục trên [a; b]. Tỉ số:
Hướng dẫn giải:
Giả sử m và M tương ứng là giá trị bé nhất và lớn nhất của hàm số f trên [a; b]
Ta có m ≤ f(x) ≤ M ∀ x ∈ [a; b]
Theo kết quả f(x) > g(x) trên đoạn [a; b] thì
Ta có:
Vì f là hàm liên tục nên tồn tại c ∈ [a; b] để
Bài 48 trang 176 SGK Toán 12 nâng cao
Giả sử một vật từ trạng thái nghỉ khi t = 0 (s) chuyển động thẳng với vận tốc v(t) = t(5 − t) (m/s). Tìm quãng đường vật đi được cho tới khi nó dừng lại.
Hướng dẫn giải:
Ta có:
Vật dừng lại tại thời điểm t = 5. Quãng đường vật đi được là
Bài 49 trang 176 SGK Toán 12 nâng cao
Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau nó đạt đến vận tốc 6 m/s. từ thời điểm đó nó chuyển động thẳng đều. Một chất điểm B xuất phát từ cùng vị trí O nhưng chậm hơn 12 giây so với A và chuyển động thẳng nhanh dần đều. biết rằng B đuổi kịp A sau 8 giây ( kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đuổi kịp A.
Hướng dẫn giải:
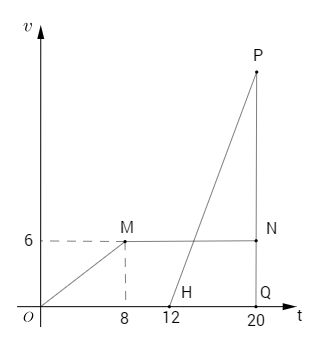
Thời điểm A và B gặp nhau là 20 giây kể từ lúc A xuất phát. Đồ thị của vận tốc của A là đường gấp khúc OMN.
Quãng đường mà A đi được (s = vt ) là diện tích hình thang OMNQ.
Vậy lúc gặp B, A đi được 96m
Đồ thị vận tốc của B là đường thẳng HP. Vì B xuất phát cùng vị trí với A nên B cũng đi được 96m . Quãng đường B đi được bằng diện tích tam giác HPQ.
Ta có
Vậy vận tốc của B tại thời điểm gặp A là 24m/s.
Bài 50 trang 176 SGK Toán 12 nâng cao
Tính các tích phân sau:
Hướng dẫn giải:
Câu a:
Đặt
Do đó:
Đặt
Do đó:
Thay (2) vào (1) ta được
Câu b:
Đặt
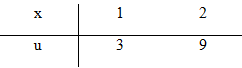
Câu c:
Đặt
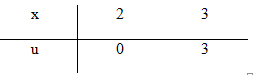
Bài 51 trang 176 SGK Toán 12 nâng cao
Tính diện tích các hình phẳng giới hạn bởi:
a) Đồ thị các hàm số y = 4 − x2; y = -x + 2
b) Các đường cong có phương trình x = 4 − 4y2 và x = 1 − y4 trong miền x ≥ 0.
Hướng dẫn giải:
Câu a:
Phương trình hoành độ giao điểm của hai đồ thị là:
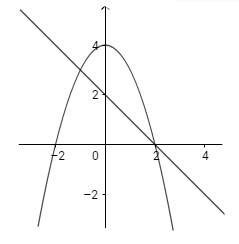
Do đó:
\(\begin{array}{l}
S = \int_{ - 1}^2 {\mid 4 - {x^2} - ( - x + 2)\mid dx} = \int_{ - 1}^2 {| - {x^2} + x + 2\mid dx} \
= \int_{ - 1}^2 {( - {x^2} + x + 2)dx} = \left. {\left( { - \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} + 2x} \right)} \right|_{ - 1}^2 = \frac{9}{2}
\end{array}\)
Câu b:
Phương trình tung độ giao điểm của hai đồ thị là
\(\begin{array}{l}
4 - 4{y^2} = 1 - {y^4} \Leftrightarrow {y^4} - 4{y^2} + 3 = 0\
\Leftrightarrow \left[ \begin{array}{l}
{y^2} = 1\
{y^2} = 3
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
y = \pm 1\
y = \pm \sqrt 3 \left( L \right)
\end{array} \right.
\end{array}\)
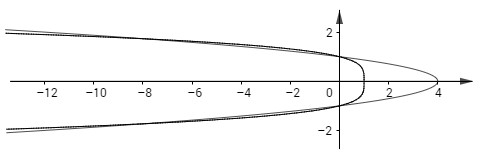
Diện tích giới hạn hai đồ thị ở phần x ≥ 0 là:
\(\begin{array}{l}
S = \int_{ - 1}^1 {[4 - 4{y^2} - (1 - {y^4})]dy} \
= \int_{ - 1}^1 {({y^4} - 4{y^2} + 3)dy} \
= \left. {\left( {\frac{{{y^5}}}{5} - \frac{4}{3}{y^3} + 3y} \right)} \right|_{ - 1}^1 = 2.\frac{{28}}{{15}} = \frac{{56}}{{15}}
\end{array}\)
Bài 52 trang 177 SGK Toán 12 nâng cao
Tính diện tích của các hình phẳng giới hạn bởi:
a) Parabol y = x2 − 2x + 2, tiếp tuyến của nó tại điểm M(3; 5) và trục tung
b) Parabol y = −x2 + 4x − 3y và các tiếp tuyến của nó tại các điểm A(0;−3)và B(3;0)
Hướng dẫn giải:
Câu a:
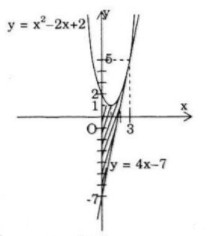
Ta có y′ = 2x − 2 => y′(3) = 4
Phương trình tiếp tuyến với parabol tại M(3;5) là:
y − 5 = 4(x − 3) <=> y = 4x − 7
Gọi S là diện tích cần tìm, ta có:
\(\begin{array}{l}
S = \int_0^3 {({x^2} - 2x + 2 - 4x + 7)dx} \
= \int_0^3 {({x^2} - 6x + 9)dx} = \int_0^3 {{{(x - 3)}^2}dx} \
= \left. {\frac{1}{3}{{\left( {x - 3} \right)}^3}} \right|_0^3 = 9
\end{array}\)
Câu b:
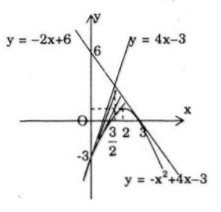
Ta có y′ = −2x + 4=> y′(0) = 4; y′(3) = −2
Phương trình tiếp tuyến tại A(0; 3) là: y + 3 = 4(x − 0) <=> y = 4x − 3
Phương trình tiếp tuyến tại B(3; 0) là: y = −2(x − 3) <=> y = −2x + 6
Giao điểm của hai tiếp tuyến là C(3/2;3). kí hiệu A1 và A2 là tam giác cong ACD Và BCD. Ta có:
\(\begin{array}{l}
S({A_1}) = \int_0^{\frac{3}{2}} {(4x - 3 + {x^2} - 4x + 3)dx} = \int_0^{\frac{3}{2}} {{x^2}dx} = \left. {\frac{{{x^3}}}{3}} \right|_0^{\frac{3}{2}} = \frac{9}{8}\
S({A_2}) = \int_{\frac{3}{2}}^3 {( - 2x + 6 + {x^2} - 4x + 3)dx} = \int_{\frac{3}{2}}^3 {{{(x - 3)}^2}dx} = \left. {\frac{1}{3}{{(x - 3)}^3}} \right|_{\frac{3}{2}}^3 = \frac{9}{8}
\end{array}\)
Vậy
Bài 53 trang 177 SGK Toán 12 nâng cao
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = 2, biết rằng thiết diện của vật thể bị cắt bơi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ (0 ≤ x ≤ 2) là một nửa hình tròn đường kính
Hướng dẫn giải:
Diện tích của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x là:
Vậy thể tích của vật thể là:
Bài 54 trang 177 SGK Toán 12 nâng cao
Xét hình phẳng giới hạn bởi đường hypebol y = 2/x và các đường thẳng y = 1, y = 4, x = 0. Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng đó quanh trục tung.
Hướng dẫn giải:
Ta có:
Thể tích cần tìm là:
Bài 55 trang 177 SGK Toán 12 nâng cao
Cho hình phẳng A được giới hạn bởi đồ thị hàm số:
Hướng dẫn giải:
Hoành độ giao điểm của hàm số
Vậy thể tích cần tìm là:
Bài 56 trang 177 SGK Toán 12 nâng cao
Cho hình phẳng A được giới hạn bởi đường cong có phương trình x(y + 1) = 2 và các đường thẳng x = 0, y = 0, y = 3. Tính thể tích khối tròn xoay tạo được khi quay A quanh trục tung.
Hướng dẫn giải:
Đường cong có phương trình là:
Vậy thể tích cần tìm là:
Bài 57 trang 177 SGK Toán 12 nâng cao
Cho hình phẳng A được giới hạn bởi đường cong có phương trình x − y2 = 0 và các đường thẳng y = 2, x = 0. Tính thể tích khối tròn xoay tạo thành khi quay A.
a) Quanh trục hoành;
b) quanh trục tung
Hướng dẫn giải:
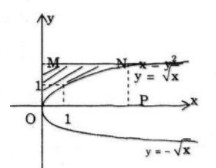
Câu a:
Hoành độ giao điểm của đường cong
Thể tích khối tròn xoay tạo thành khi quay A quanh Ox là:
Câu b:
Thể tích khối tròn xoay tạo thành khi quay A quanh Oy là:
Bài 58 trang 177 SGK Toán 12 nâng cao
Cho hình phẳng A được giới hạn bởi đường cong có phương trình
Hướng dẫn giải:
Thể tích cần tìm là:
Đặt
Do đó:
Bài 59 trang 177 SGK Toán 12 nâng cao
Cho hình phẳng A được giới hạn bởi đường cong có phương trình y2 = x3 và các đường thẳng y = 0, x = 1. Tính thể tích khối tròn xoay tạo được khi quay A
a) Quanh trục hoành
b) Quanh trục tung.
Hướng dẫn giải:
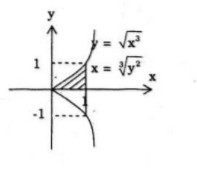
Câu a:
Ta có:
Thể tích cần tìm là:
Câu b:
Ta có:
Thể tích cần tìm là:
Trên đây là nội dung hướng dẫn giải chi tiết bài tập SGK nâng cao môn Toán 12 Ôn tập Chương 3 Nguyên hàm, tích phân và ứng dụng được trình bày rõ ràng, cụ thể với phương pháp ngắn gọn và khoa học. Hy vọng rằng đây sẽ là tài liệu hữu ích giúp các em học sinh lớp 12 học tập thật tốt!






Thảo luận về Bài viết