Bài 1 trang 81 SGK Hình học 12 nâng cao
Cho vecto \(\vec u = \vec i - 2\vec j{\mkern 1mu} {\kern 1pt} ;{\mkern 1mu} {\kern 1pt} \vec v = 3\vec i + 5\left( {\vec j - \vec k} \right){\mkern 1mu} {\kern 1pt} ;{\mkern 1mu} {\kern 1pt} {\rm{\vec w}} = 2\vec i - \vec k + 3\vec j\)
a) Tìm toạ độ của các vectơ đó.
b) Tìm côsin của các góc \(\left( {\vec v,\vec i} \right){\mkern 1mu} {\kern 1pt} ;{\mkern 1mu} {\kern 1pt} \left( {\vec v,\vec j} \right){\mkern 1mu} {\kern 1pt} ;{\mkern 1mu} {\kern 1pt} \left( {\vec v,\vec k} \right)\)
c) Tính các tích vô hướng \(\vec u.\vec v{\mkern 1mu} {\kern 1pt} ,{\mkern 1mu} {\kern 1pt} \vec u.{\rm{\vec w}}{\mkern 1mu} {\kern 1pt} ,{\mkern 1mu} {\kern 1pt} \vec v.{\rm{\vec w}}\)
Hướng dẫn giải:
Câu a:
\(\vec u = \left( {1; - 2;0} \right){\mkern 1mu} {\kern 1pt} ;{\mkern 1mu} {\kern 1pt} \vec v = \left( {3;5; - 5} \right){\mkern 1mu} {\kern 1pt} ;{\mkern 1mu} {\kern 1pt} {\rm{\vec w}} = \left( {2;3; - 1} \right)\)
Câu b:
\(\begin{array}{l}
\cos \left( {\overrightarrow v ;\overrightarrow i } \right) = \frac{{\overrightarrow v .\overrightarrow i }}{{|\overrightarrow v ||\overrightarrow i |}} = \frac{3}{{\sqrt {59} }}\\
\cos \left( {\overrightarrow v ;\overrightarrow j } \right) = \frac{{\overrightarrow v .\overrightarrow j }}{{|\overrightarrow v ||\overrightarrow j |}} = \frac{5}{{\sqrt {59} }}\\
\cos \left( {\overrightarrow v ;\overrightarrow k } \right) = \frac{{\overrightarrow v .\overrightarrow k }}{{|\overrightarrow v ||\overrightarrow k |}} = \frac{{ - 5}}{{\sqrt {59} }}
\end{array}\)
Câu c:
\(\begin{array}{l}
\vec u = \left( {1; - 2;0} \right){\mkern 1mu} {\kern 1pt} ;{\mkern 1mu} {\kern 1pt} \vec v = \left( {3;5; - 5} \right){\mkern 1mu} {\kern 1pt} ;{\mkern 1mu} {\kern 1pt} {\rm{\vec w}} = \left( {2;3; - 1} \right)\\
\overrightarrow u .\overrightarrow v = 1.3 - 2.5 + 0( - 5) = - 7\\
\overrightarrow u .\overrightarrow w = 1.2 - 2.3 + 0( - 1) = - 4\\
\overrightarrow v .\overrightarrow w = 3.2 + 5.3 + ( - 5).( - 1) = 26
\end{array}\)
Bài 2 trang 81 SGK Hình học 12 nâng cao
Cho vecto \(\overrightarrow u \) tùy ý khác \(\overrightarrow 0 \). Chứng minh \(co{s^2}(\overrightarrow u ,\overrightarrow i ) + co{s^2}(\overrightarrow u ,\overrightarrow j ) + co{s^2}(\overrightarrow u ,\overrightarrow k ) = 1\)
Hướng dẫn giải:
Giả sử \(\overrightarrow u = \left( {x;y;z} \right)\)
\(\begin{array}{l}
cos(\overrightarrow u ,\overrightarrow i ) = \frac{{\overrightarrow u .\overrightarrow i }}{{|\overrightarrow u ||\overrightarrow i |}} = \frac{x}{{\sqrt {{x^2} + {y^2} + {z^2}} }} \Rightarrow {\cos ^2}(\overrightarrow u ,\overrightarrow i ) = \frac{{{x^2}}}{{{x^2} + {y^2} + {z^2}}}\\
{\cos ^2}(\overrightarrow u ,\overrightarrow j ) = \frac{{{y^2}}}{{{x^2} + {y^2} + {z^2}}};{\cos ^2}(\overrightarrow u ,\overrightarrow k ) = \frac{{{z^2}}}{{{x^2} + {y^2} + {z^2}}}
\end{array}\)
Vậy \({\rm{\backslash }}(co{s^2}(\vec u,\vec i) + co{s^2}(\vec u,\vec j) + co{s^2}(\vec u,\vec k) = \frac{{{x^2} + {y^2} + {z^2}}}{{{x^2} + {y^2} + {z^2}}} = 1\)
Bài 3 trang 81 SGK Hình học 12 nâng cao
Tìm góc giữa hai vecto \(\vec u\) và \(\vec v\) trong mỗi trường hợp sau:
a) \(\overrightarrow u = \left( {1;1;1} \right);\overrightarrow v = \left( {2;1; - 1} \right)\)
b) \(\vec u = 3\vec i + 4\vec j{\mkern 1mu} {\kern 1pt} {\mkern 1mu} {\kern 1pt} ;{\mkern 1mu} {\kern 1pt} {\mkern 1mu} {\kern 1pt} \vec v = - 2\vec j + 3\vec k\)
Hướng dẫn giải:
Câu a:
\(\cos \left( {\overrightarrow u ;\overrightarrow v } \right) = \frac{{\overrightarrow u .\overrightarrow v }}{{|\overrightarrow u ||\overrightarrow v |}} = \frac{2}{{\sqrt 3 .\sqrt 6 }} = \frac{{\sqrt 2 }}{3}\)
Câu b:
\(\begin{array}{l}
\overrightarrow u = \left( {3;4;9} \right);\overrightarrow v = \left( {0; - 2;3} \right)\\
\Rightarrow \cos \left( {\overrightarrow u ;\overrightarrow v } \right) = \frac{{\overrightarrow u .\overrightarrow v }}{{|\overrightarrow u ||\overrightarrow v |}} = \frac{{ - 8\sqrt {13} }}{{65}}
\end{array}\)
Bài 4 trang 81 SGK Hình học 12 nâng cao
Biết \(|\overrightarrow u | = 2;|\overrightarrow v | = 5\), góc giữa vecto \({\vec u}\) và \({\vec v}\) bằng \(\frac{{2\pi }}{3}\). Tìm vecto \(\overrightarrow p = k\overrightarrow u + 17\overrightarrow v \) vuông góc với vecto \(\overrightarrow q = 3\overrightarrow u - \overrightarrow v \)
Hướng dẫn giải:
Ta có:
\(\begin{array}{l}
cos(\overrightarrow u ,\overrightarrow v ) = cos\frac{{2\pi }}{3} = - \frac{1}{2};\overrightarrow p \bot \overrightarrow q \\
\overrightarrow p .\overrightarrow q = 0 \Leftrightarrow \left( {k\overrightarrow u + 17\overrightarrow v } \right)\left( {3\overrightarrow u - \overrightarrow v } \right) = 0\\
\Leftrightarrow 3k|\overrightarrow u {|^2} - 17|\overrightarrow v {|^2} + \left( {51 - k} \right)\overrightarrow u .\overrightarrow v = 0\\
\Leftrightarrow 3k.4 - 17.25 + (51 - k).2.5.\left( { - \frac{1}{2}} \right) = 0\\
\Leftrightarrow 17k - 680 = 0\\
\Leftrightarrow k = 40
\end{array}\)
Vậy với k = 0 thì \(\overrightarrow p \bot \overrightarrow q \)
Bài 5 trang 81 SGK Hình học 12 nâng cao
Cho điểm M(a; b; c)
a) Tìm toạ độ hình chiếu (vuông góc) của M trên các mặt phẳng toạ độ và trên các trục toạ độ.
b) Tìm khoảng cách từ điểm M đến các mặt phẳng toạ độ, đến các trục toạ độ.
c) Tìm toạ độ của các điểm đối xứng với M qua các mặt phẳng toạ độ.
Hướng dẫn giải:
Câu a:
Gọi M1(x; y; 0) là hình chiếu của điểm M(a;b;c) trên mp(Oxy) thì \(\overrightarrow {M{M_1}} = \left( {x - a,y - b, - c} \right);\overrightarrow {M{M_1}} .\vec i = \overrightarrow {M{M_1}} .\vec j = 0\) nên
\(\left\{ \begin{array}{l}
x - a = 0\\
y - b = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = a\\
y = b
\end{array} \right. \Rightarrow {M_1}(a;b;0)\)
Tương tự M2(0; b; c) là hình chiếu của M(a; b; c) trên mp(Oyz)
Và M3(a; 0; c) là hình chiếu của M(a;b;c) trên mp(Oxz).
Giả sử M4(x; 0; 0) là hình chiếu của M(a; b; c) trên trục Ox thì
\(\overrightarrow {M{M_4}} = \left( {x - a; - b; - c} \right);\overrightarrow {M{M_4}} .\overrightarrow i = 0\) nên x = a.
Vậy \({M_4}\left( {a;0;0} \right)\)
Tương tự M5(0; b; 0) và M6(0; 0; c) lần lượt là hình chiếu của M(a; b; c) trên trục Oy và Oz.
Câu b:
Khoảng cách từ M đến (Oxy) là:
\(\begin{array}{l}
d(M;(Oxy)) = M{M_1} = \sqrt {{{(a - a)}^2} + {{(b - b)}^2} + {{(c - 0)}^2}} = |c|\\
d(M;(Oyz)) = |a|;d(M;(Oxz)) = |b|\\
d(M;Ox) = M{M_4} = \sqrt {{{(a - a)}^2} + {{(b - 0)}^2} + {{(c - 0)}^2}} = \sqrt {{b^2} + {c^2}} \\
d(M;Oy) = \sqrt {{a^2} + {c^2}} ,d(M;Oz) = \sqrt {{a^2} + {b^2}}
\end{array}\)
Câu c:
Gọi M′1(x; y; z) là điểm đối xứng của M qua mp(Oxy) thì M1 là trung điểm của MM′1 nên
.jpg?enablejsapi=1)
Tương tự M′2(−a; b; c) là điểm đối xứng của M qua mp(Oyz)
Và M′3(a; −b; c) là điểm đối xứng của M qua mp(Oxz)
Bài 6 trang 81 SGK Hình học 12 nâng cao
Cho hai điểm A(x1; y1; z1) và B(x2; y2; z2). Tìm toạ độ điểm M chia đoạn thẳng AB theo tỉ số k (tức là \(\overrightarrow {MA} = k\overrightarrow {MB} \)), trong đó k ≠ 1
Hướng dẫn giải:
Giả sử M(x; y; z) thỏa mãn \(\overrightarrow {MA} = k\overrightarrow {MB} \) với k ≠ 1
Ta có:
\(\begin{array}{l}
\overrightarrow {MA} = ({x_1} - x;{y_1} - y;{z_1} - z);\overrightarrow {MB} = ({x_2} - x;{y_2} - y;{z_2} - z)\\
\overrightarrow {MA} = k\overrightarrow {MB} \Leftrightarrow \left\{ \begin{array}{l}
{x_1} - x = k({x_2} - x)\\
{y_1} - y = k({y_2} - y)\\
{z_1} - z = k({z_2} - z)
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = \frac{{{x_1} - k{x_2}}}{{1 - k}}\\
y = \frac{{{y_1} - k{y_2}}}{{1 - k}}\\
z = \frac{{{z_1} - k{z_2}}}{{1 - k}}
\end{array} \right.
\end{array}\)
Bài 7 trang 81 SGK Hình học 12 nâng cao
Cho hình bình hành ABCD với A(-3 ; -2 ; 0), B(3 ; -3 ; 1), C(5 ; 0 ; 2). Tìm toạ độ đỉnh D và tính góc giữa hai vectơ \(\overrightarrow {AC} ,\overrightarrow {BD} \)
Hướng dẫn giải:
Ta có \(\overrightarrow {BA} = ( - 6;1; - 1);\overrightarrow {BC} = (2;3;1)\). Vì \(\frac{{ - 6}}{2} \ne \frac{1}{3} \ne \frac{{ - 1}}{1}\) nên \(\overrightarrow {BA} ;\overrightarrow {BC} \) không cùng phương nên ba điểm A, B, C không thẳng hàng.
Giả sử D(x; y; z) thì \(\overrightarrow {BD} = (x - 3;y + 3;z - 1)\)
ABCD là hình bình hành khi và chỉ khi:
\(\overrightarrow {BD} = \overrightarrow {BA} + \overrightarrow {BC} \Leftrightarrow \left\{ \begin{array}{l}
x - 3 = - 6 + 2\\
y + 3 = 1 + 3\\
z - 1 = - 1 + 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = - 1\\
y = 1\\
z = 1
\end{array} \right.\)
Vậy D(−1; 1; 1). Ta có \(\overrightarrow {AC} = \left( {8;2;2} \right){\mkern 1mu} {\kern 1pt} ;{\mkern 1mu} {\kern 1pt} \overrightarrow {BD} = \left( { - 4;4;0} \right)\)
Do đó:
\(\begin{array}{l}
cos\left( {\overrightarrow {AC} ;{\mkern 1mu} {\kern 1pt} \overrightarrow {BD} } \right) = \frac{{\overrightarrow {AC} .{\mkern 1mu} {\kern 1pt} \overrightarrow {BD} }}{{AC.BD}} = \frac{{ - 32 + 8}}{{\sqrt {72} .\sqrt {32} }} = - \frac{1}{2}\\
\Rightarrow \left( {\overrightarrow {AC} ;{\mkern 1mu} {\kern 1pt} \overrightarrow {BD} } \right) = \frac{{2\pi }}{3}
\end{array}\)
Bài 8 trang 81 SGK Hình học 12 nâng cao
a) Tìm toạ độ điểm M thuộc trục Ox sao cho M cách đều hai điểm A(1 ; 2 ; 3) và B(-3 ; -3 ; 2).
b) Cho ba điểm A(2; 0; 4); B(4; \(\sqrt 3 \); 5) và C(sin5t, cos3t, sin3t). Tìm t để AB vuông góc với OC (O là gốc toạ độ).
Hướng dẫn giải:
Câu a:
Giả sử M(x; 0; 0) thuộc trục Ox và MA = MB.
Ta có:
\(\begin{array}{l}
M{A^2} = M{B^2}\\
\Leftrightarrow {(1 - x)^2} + {2^2} + {3^2} = {( - 3 - x)^2} + {( - 3)^2} + {2^2}\\
\Leftrightarrow 1 - 2x + {x^2} + 13 = 9 + 6x + {x^2} + 13 \Leftrightarrow x = - 1\\
\Rightarrow M( - 1;0;0)
\end{array}\)
Câu b:
Ta có:
\(\begin{array}{l}
\overrightarrow {AB} = (2;\sqrt 3 ;1);\overrightarrow {OC} = (sin5t;cos3t;sin3t)\\
AB \bot OC \Leftrightarrow \overrightarrow {AB} .\overrightarrow {OC} = 0\\
\Leftrightarrow 2sin5t + \sqrt 3 cos3t + sin3t = 0\\
\Leftrightarrow sin5t + \frac{{\sqrt 3 }}{2}cos3t + \frac{1}{2}sin3t = 0\\
\Leftrightarrow sin5t = - sin\left( {3t + \frac{\pi }{3}} \right)\\
\Leftrightarrow sin5t = sin\left( { - 3t - \frac{\pi }{3}} \right)\\
\Leftrightarrow \left[ \begin{array}{l}
5t = - 3t - \frac{\pi }{3} + k2\pi \\
5t = \pi + 3t + \frac{\pi }{3} + k2\pi
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
t = - \frac{\pi }{{24}} + \frac{{k\pi }}{4}\\
t = \frac{{2\pi }}{3} + k\pi
\end{array} \right.(k \in Z)
\end{array}\)
Bài 9 trang 81 SGK Hình học 12 nâng cao
Xét sự đồng phẳng của ba vectơ \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w \) trong mỗi trường hợp sau:
\(\begin{array}{l}
a)\overrightarrow u (4;3;4),\overrightarrow v (2; - 1;2),\overrightarrow w (1;2;1)\\
b)\overrightarrow u (1; - 1;1),\overrightarrow v (0;1;2),\overrightarrow w (4;2;3)\\
c)\overrightarrow u (4;2;5),\overrightarrow v (3;1;3),\overrightarrow w (2;0;1)
\end{array}\)
Hướng dẫn giải:
Câu a:
Ta có:
\(\begin{array}{l}
\left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( {\left| {\begin{array}{*{20}{c}}
3&4\\
{ - 1}&2
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
4&4\\
2&2
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
4&3\\
2&{ - 1}
\end{array}} \right|} \right) = \left( {10;0; - 10} \right)\\
\Rightarrow \left[ {\overrightarrow u ,\overrightarrow v } \right].\overrightarrow w = 10.1 + 0.2 - 10.1 = 0
\end{array}\)
Do đó \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w \) đồng phẳng
Câu b:
\(\left[ {\overrightarrow u ,\overrightarrow v } \right].\overrightarrow w \ne 0 \Rightarrow \) \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w \) không đồng phẳng
Câu c:
\(\left[ {\overrightarrow u ,\overrightarrow v } \right].\overrightarrow w = 0 \Rightarrow \) \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w \) đồng phẳng
Bài 10 trang 81 SGK Hình học 12 nâng cao
Cho ba điểm A(1; 0; 0); B(0; 0; 1); C(2; 1; 1)
a) Chứng minh A, B, C không thẳng hàng.
b) Tính chu vi và diện tích tam giác ABC.
c) Tính độ dài đường cao của tam giác ABC kẻ từ đỉnh A.
d) Tính các góc của tam giác ABC.
Hướng dẫn giải:
Câu a:
Ta có: \(\overrightarrow {BA} = \left( {1;0; - 1} \right),\overrightarrow {BC} = \left( {2;1;0} \right)\)
Vì \(\frac{1}{2} \ne \frac{0}{1} \Rightarrow \overrightarrow {BA} ;\overrightarrow {BC} \) không cùng phương do đó A, B, C thẳng hàng.
Câu b:
\(\begin{array}{l}
AB = \sqrt {{1^2} + {0^2} + {{( - 1)}^2}} = \sqrt 2 \\
BC = \sqrt {{2^2} + {1^2} + {0^2}} = \sqrt 5 \\
AC = \sqrt {{1^2} + {1^2} + {1^2}} = \sqrt 3
\end{array}\)
Vậy chu vi tam giác ABC bằng \(\sqrt 2 + \sqrt 3 + \sqrt 5 \)
Ta có: \(B{C^2} = A{B^2} + A{C^2} \Rightarrow \Delta ABC\) vuông tại A nên có diện tích \(S = \frac{1}{2}AB.AC = \frac{{\sqrt 6 }}{2}\)
Câu c:
Gọi ha là độ dài đường cao kẻ từ A ta có:
\({S_{ABC}} = \frac{1}{2}BC.{h_a} \Rightarrow {h_a} = \frac{{2{S_{ABC}}}}{{BC}} = \frac{{\sqrt 6 }}{{\sqrt 5 }} = \frac{{\sqrt {30} }}{5}\)
Câu d:
Vì tam giác ABC vuông tại A nên:
\(\begin{array}{l}
cosB = \frac{{AB}}{{BC}} = \frac{{\sqrt 2 }}{{\sqrt 5 }} = \frac{{\sqrt {10} }}{5}\\
cosC = \frac{{AC}}{{BC}} = \frac{{\sqrt 3 }}{{\sqrt 5 }} = \frac{{\sqrt {15} }}{5}
\end{array}\)
Bài 11 trang 81 SGK Hình học 12 nâng cao
Cho bốn điểm A(1 ; 0 ; 0), B(0 ; 1 ; 0), C(0 ; 0 ; 1) và D(-2 ; 1 ; -2).
a) Chứng minh rằng A, B, C, D là bốn đỉnh của một hình tứ diện.
b) Tính góc giữa các đường thẳng chứa các cạnh đối của tứ diện đó.
c) Tính thể tích tứ diện ABCD và độ dài đường cao của tứ diện kẻ từ đỉnh A
Hướng dẫn giải:
Câu a:
Ta có:
\(\begin{array}{l}
\overrightarrow {AB} = ( - 1;1;0),\overrightarrow {AC} = ( - 1;0;1),\overrightarrow {AD} = ( - 3;1; - 2)\\
\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}
1&0\\
0&1
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
0&{ - 1}\\
1&{ - 1}
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
{ - 1}&1\\
{ - 1}&0
\end{array}} \right|} \right) = \left( { - 3;1; - 2} \right)\\
\Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right].\overrightarrow {AD} = - 3.1 + 1.1 - 2.1 = - 4 \ne 0
\end{array}\)
Do đó 3 vecto \(\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {AD} \) không đồng phẳng. Vậy A, B, C, D là 4 đỉnh của một tứ diện.
Câu b:
Ta có \(\overrightarrow {CD} = \left( { - 2;1; - 3} \right),\overrightarrow {BD} = \left( { - 2;0; - 2} \right),\overrightarrow {BC} = \left( {0; - 1;1} \right)\)
Gọi α, β, γ lần lượt là góc tạo bởi các cặp đường thẳng AB và CD, AC và BD, AD và BC thì
\(\begin{array}{l}
cos\alpha = \left| {\cos \left( {\overrightarrow {AD} ;\overrightarrow {CD} } \right)} \right| = \frac{{|2 + 1 + 0|}}{{\sqrt 2 .\sqrt {14} }} = \frac{{3\sqrt 7 }}{{14}}\\
cos\beta = \left| {\cos \left( {\overrightarrow {AC} ;\overrightarrow {BD} } \right)} \right| = \frac{{|2 + 0 - 2|}}{{\sqrt 2 .\sqrt 8 }} = 0 \Rightarrow AC \bot BD\\
cos\gamma = \left| {\cos \left( {\overrightarrow {AD} ;\overrightarrow {BC} } \right)} \right| = \frac{{|0 - 1 - 2|}}{{\sqrt 2 .\sqrt {14} }} = \frac{{3\sqrt 7 }}{{14}}
\end{array}\)
Câu c:
Thể tích của tứ diện ABCD là: \(V = \frac{1}{6}\left| {\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right].\overrightarrow {AD} } \right| = \frac{1}{6}| - 4| = \frac{2}{3}\)
Gọi hA là đường cao của tứ diện kẻ từ đỉnh A.
Ta có:
\(\begin{array}{l}
V = \frac{1}{3}{h_A}.{S_{BCD}} \Rightarrow {h_A} = \frac{{3V}}{{{S_{BCD}}}}\\
{S_{BCD}} = \frac{1}{2}\left| {\left[ {\overrightarrow {BC} ;\overrightarrow {BD} } \right]} \right| = \sqrt 3 \\
\Rightarrow {h_A} = \frac{{3.\frac{2}{3}}}{{\sqrt 3 }} = \frac{{2\sqrt 3 }}{3}
\end{array}\)
Bài 12 trang 82 SGK Hình học 12 nâng cao
Cho hình chóp S.ABC có đường cao SA = h, đáy là tam giác ABC vuông tại C, AC = b, BC = a. Gọi M là trung điểm của AC và N là điểm sao cho \(\overrightarrow {SN} = \frac{1}{3}\overrightarrow {SB} \)
a) Tính độ dài đoạn thẳng MN.
b) Tìm sự liên hệ giữa a, b, h để MN vuông góc với SB.
Hướng dẫn giải:
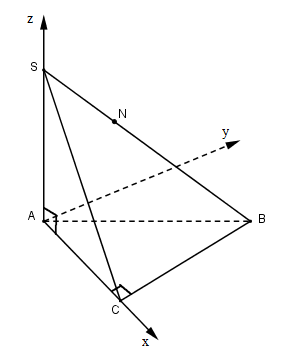
Chọn hệ trục Oxyz như hình vẽ, B nằm trong góc xOy.
Ta có: A = (0; 0; 0), C = (b; 0; 0), B = (b; a; 0), S = (0; 0; h).
\(M\left( {\frac{b}{2};0;0} \right),\overrightarrow {SB} = (b;a; - h)\)
Gọi N(x; y; z) thì \(\overrightarrow {SN} = \left( {x;y;z - h} \right)\)
\(\overrightarrow {SN} = \frac{1}{3}\overrightarrow {SB} \Leftrightarrow \left\{ \begin{array}{l}
x = \frac{b}{3}\\
y = \frac{a}{3}\\
z - h = \frac{{ - h}}{3}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = \frac{b}{3}\\
y = \frac{a}{3}\\
z = \frac{{2h}}{3}
\end{array} \right. \Rightarrow N\left( {\frac{b}{3};\frac{a}{3};\frac{{2h}}{3}} \right)\)
Câu a:
\(\begin{array}{l}
\overrightarrow {MN} = \left( {\frac{b}{3} - \frac{b}{2};\frac{a}{3};\frac{{2h}}{3}} \right) = \left( { - \frac{b}{6};\frac{a}{3};\frac{{2h}}{3}} \right)\\
MN = \sqrt {\frac{{{b^2}}}{{36}} + \frac{{{a^2}}}{9} + \frac{{4{h^2}}}{9}} = \frac{1}{6}\sqrt {{b^2} + 4{a^2} + 16{h^2}}
\end{array}\)
Câu b:
\(\begin{array}{l}
MN \bot SB \Leftrightarrow \overrightarrow {MN} .\overrightarrow {SB} = 0\\
\Leftrightarrow - \frac{{{b^2}}}{6} + \frac{{{a^2}}}{3} + \frac{{ - 2{h^2}}}{3} = 0\\
\Leftrightarrow 4{h^2} = 2{a^2} - {b^2}
\end{array}\)
Bài 13 trang 82 SGK Hình học 12 nâng cao
Tìm toạ độ tâm và tính bán kính của mỗi mặt cầu sau đây :
\(\begin{array}{l}
a){x^2} + {y^2} + {z^2} - 8x + 2y + 1 = 0\\
b)3{x^2} + 3{y^2} + 3{z^2} + 6x - 3y + 15z - 2 = 0\\
c)9{x^2} + 9{y^2} + 9{z^2} - 6x + 18y + 1 = 0
\end{array}\)
Hướng dẫn giải:
Câu a:
\(\begin{array}{l}
{x^2} + {y^2} + {z^2} - 8x + 2y + 1 = 0\\
\Leftrightarrow ({x^2} - 8x + 16) + ({y^2} + 2y + 1) + {z^2} = 16\\
\Leftrightarrow {(x - 4)^2} + {(y + 1)^2} + {z^2} = 16
\end{array}\)
Mặt cầu có tâm I(4; −1; 0) và có bán kính R = 4.
Câu b:
\(\begin{array}{l}
3{x^2} + 3{y^2} + 3{z^2} + 6x - 3y + 15z - 2 = 0\\
\Leftrightarrow {x^2} + {y^2} + {z^2} + 2x - y + 5z - 23 = 0\\
\Leftrightarrow {(x + 1)^2} + {\left( {y - \frac{1}{2}} \right)^2} + {\left( {z + \frac{5}{2}} \right)^2} = \frac{{49}}{6}
\end{array}\)
Mặt cầu có tâm \(I\left( { - 1;\frac{1}{2}; - \frac{5}{2}} \right)\) và có bán kính \(R = \frac{{7\sqrt 6 }}{6}\)
Câu c:
\(\begin{array}{l}
9{x^2} + 9{y^2} + 9{z^2} - 6x + 18y + 1 = 0\\
\Leftrightarrow {x^2} + {y^2} + {z^2} - \frac{2}{3}x + 2y + \frac{1}{9} = 0\\
\Leftrightarrow {\left( {x - \frac{1}{3}} \right)^2} + {(y + 1)^2} + {z^2} = 1
\end{array}\)
Mặt cầu có tâm \(I\left( {\frac{1}{3}; - 1;0} \right)\) và có bán kính R = 1
Bài 14 trang 82 SGK Hình học 12 nâng cao
Trong mỗi trường hợp sau, hãy viết phương trình mặt cầu :
a) Đi qua ba điểm A(0 ; 8 ; 0), B(4; 6 ; 2), C(0 ; 12 ; 4) và có tâm nằm trên mp(Oyz);
b) Có bán kính bằng 2, tiếp xúc với mặt phẳng (Oyz) và có tâm nằm trên tia Ox;
c) Có tâm I(1 ; 2 ; 3) và tiếp xúc với mp(Oyz).
Hướng dẫn giải:
Câu a:
Tâm I của mặt cầu nằm trên mp(Oyz) nên I(0; b; c) Ta tìm b và c để IA = IB = IC. Ta có:
\(\left\{ \begin{array}{l}
I{A^2} = I{B^2}\\
I{A^2} = I{C^2}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{(8 - b)^2} + {c^2} = {4^2} + {(6 - b)^2} + {(2 - c)^2}\\
{(8 - b)^2} + {c^2} = {(12 - b)^2} + {(4 - c)^2}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
b = 7\\
c = 5
\end{array} \right.\)
Vậy tâm I(0; 7; 5) bán kính \(R = IA = \sqrt {0 + 1 + 25} = \sqrt {26} \)
Mặt cầu có phương trình \({x^2} + {\left( {y - 7} \right)^2} + {\left( {z - 5} \right)^2} = 26\)
Câu b:
Vì tâm của mặt cầu nằm trên tia Ox và mặt cầu tiếp xúc với mp(Oyz) nên điểm tiếp xúc phải là O, do đó bán kính mặt cầu là R = IO = 2 và I(2; 0; 0).
Mặt cầu có phương trình \({(x - 2)^2} + {y^2} + {z^2} = 4\)
Câu c:
Vì mặt cầu có tâm I(1; 2; 3) và tiếp xúc với mp(Oyz), vậy R = 1. Mặt cầu có phương trình
\({(x - 1)^2} + {(y - 2)^2} + {(z - 3)^2} = 1\)
Trên đây là nội dung hướng dẫn giải chi tiết bài tập SGK nâng cao môn Toán 12 Chương 3 Bài 1 Hệ tọa độ trong không gian được trình bày rõ ràng, cụ thể với phương pháp ngắn gọn và khoa học. Hy vọng rằng đây sẽ là tài liệu hữu ích giúp các em học sinh lớp 12 học tập thật tốt!
