Giải Toán 11 SGK nâng cao Chương 4 Bài 2 Dãy số có giới hạn hữu hạn

Tìm các giới hạn sau:

a) \(\lim \left( {2 + \frac{{{{\left( { - 1} \right)}^n}}}{{n + 2}}} \right)\)

b) \(\lim \left( {\frac{{\sin 3n}}{{4n}} - 1} \right)\)

c) \(\lim \frac{{n - 1}}{n}\)

d) \(\lim \frac{{n + 2}}{{n + 1}}\)

Hướng dẫn giải:

Câu a:

Đặt \({u_n} = 2 + \frac{{{{\left( { - 1} \right)}^n}}}{{n + 2}}\), ta có:

\(\left| {{u_n} - 2} \right| = \frac{1}{{n + 2}} < \frac{1}{n}\) và \(\lim \frac{1}{n} = 0 \Rightarrow \lim \left( {{u_n} - 2} \right) = 0 \Rightarrow \lim {u_n} = 2\)

Câu b:

Đặt \({u_n} = \frac{{\sin 3n}}{{4n}} - 1\)

Ta có \(\left| {{u_n} + 1} \right| = \left| {\frac{{\sin 3n}}{{4n}}} \right| \le \frac{1}{{4n}}\) và \(\lim \frac{1}{{4n}} = 0 \Rightarrow \lim \left( {{u_n} + 1} \right) = 0 \Rightarrow \lim {u_n} =  - 1\)

Câu c:

Ta có \(\lim \frac{{n - 1}}{n} = \lim \left( {1 - \frac{1}{n}} \right) = \lim 1 - \lim \frac{1}{n} = 1\)

Câu d:

\(\lim \frac{{n + 2}}{{n + 1}} = \lim \frac{{n\left( {1 + \frac{2}{n}} \right)}}{{n\left( {1 + \frac{1}{n}} \right)}} = \lim \frac{{1 + \frac{2}{n}}}{{1 + \frac{1}{n}}} = 1\)

---

Tìm \(\lim u_n\) với:

a) \({u_n} = \frac{{{n^2} - 3n + 5}}{{2{n^2} - 1}}\)

b) \({u_n} = \frac{{ - 2{n^2} + n + 2}}{{3{n^4} + 5}}\)

c) \({u_n} = \frac{{\sqrt {2{n^2} - n} }}{{1 - 3{n^2}}}\)

d) \({u_n} = \frac{{{4^n}}}{{{{2.3}^n} + {4^n}}}\)

Hướng dẫn giải:

Câu a:

Ta có:

\(\begin{array}{l}
\lim {u_n} = \lim \frac{{{n^2}\left( {1 - \frac{3}{n} + \frac{5}{{{n^2}}}} \right)}}{{{n^2}\left( {2 - \frac{1}{{{n^2}}}} \right)}} = \lim \frac{{1 - \frac{3}{n} + \frac{5}{{{n^2}}}}}{{2 - \frac{1}{{{n^2}}}}}\\
 = \frac{{\lim 1 - \lim \frac{3}{n} + \lim \frac{5}{{{n^2}}}}}{{\lim 2 - \lim \frac{1}{{{n^2}}}}} = \frac{{1 - 0 + 0}}{{2 - 0}} = \frac{1}{2}
\end{array}\)

Câu b:

Ta có \(\lim {u_n} = \lim \frac{{{n^4}\left( {\frac{{ - 2}}{{{n^2}}} + \frac{1}{{{n^3}}} + \frac{2}{{{n^4}}}} \right)}}{{{n^4}\left( {3 + \frac{5}{{{n^4}}}} \right)}} = \lim \frac{{\frac{{ - 2}}{{{n^2}}} + \frac{1}{{{n^3}}} + \frac{2}{{{n^4}}}}}{{3 + \frac{5}{{{n^4}}}}} = \frac{0}{3} = 0\)

Câu c:

\(\lim {u_n} = \lim \frac{{{n^2}\sqrt {\frac{2}{{{n^2}}} - \frac{1}{{{n^3}}}} }}{{{n^2}\left( {\frac{1}{{{n^2}}} - 3} \right)}} = \lim \frac{{\sqrt {\frac{2}{{{n^2}}} - \frac{1}{{{n^3}}}} }}{{\left( {\frac{1}{{{n^2}}} - 3} \right)}} = \frac{0}{{ - 3}} = 0\)

Câu d:

Chia cả tử và mẫu u_n cho 4ⁿ ta được:

\(\lim {u_n} = \lim \frac{1}{{2.{{\left( {\frac{3}{4}} \right)}^n} + 1}} = 1\) (vì \(\lim {\left( {\frac{3}{4}} \right)^n} = 0\))

---

Cho dãy số (un) xác định bởi

u₁ = 10 và \({u_{n + 1}} = \frac{{{u_n}}}{5} + 3\) và \({u_{n + 1}} = \frac{{{u_n}}}{5} + 3\) với mọi n ≥ 1

a. Chứng minh rằng dãy số (v_n) xác định bởi \({v_n} = {u_n} - \frac{{15}}{4}\) là một cấp số nhân.

b. Tìm \(\lim u_n\).

Hướng dẫn giải:

Câu a:

Ta có \({v_{n + 1}} = {u_{n + 1}} - \frac{{15}}{4} = \frac{{{u_n}}}{5} + 3 - \frac{{15}}{4} = \frac{{{u_n}}}{5} - \frac{3}{4}\)

Thay \({u_n} = {v_n} + \frac{{15}}{4}\) vào ta được:

\({v_{n + 1}} = \frac{1}{5}\left( {{v_n} + \frac{{15}}{4}} \right) - \frac{3}{4} = \frac{1}{5}{v_n},\forall n\)

Vậy (v_n) là cấp số nhân lùi vô hạn với công bội \(q = \frac{1}{5}\)

Câu b:

\(\begin{array}{l}
{v_1} = {u_1} - \frac{{15}}{4} = 10 - \frac{{15}}{4} = \frac{{25}}{4}\\
{v_n} = {v_1}.{q^{n - 1}} = \frac{{25}}{4}.{\left( {\frac{1}{5}} \right)^{n - 1}}\\
 \Rightarrow \lim {v_n} = 0 \Rightarrow \lim {u_n} = \frac{{15}}{4}
\end{array}\)

---

Cho một tam giác đều ABC cạnh a. Tam giác A₁B₁C₁ có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A₂B₂C₂ có các đỉnh là trung điểm các cạnh của tam giác A₁B₁C₁,…, tam giác A_n+1B_n+1C_n+1 có các đỉnh là trung điểm các cạnh của tam giác A_nB_nC_n, … . Gọi p₁, p₂, ..., p_n, … và S₁, S₂, …, S_n, … theo thứ tự là chu vi và diện tích của các tam giác.

a. Tìm giới hạn của các dãy số (p_n) và (S_n).

b. Tìm các tổng p₁+p₂+...+p_n+... và S₁+S₂+...+S_n+...

Hướng dẫn giải:

Câu a:

Ta có \({p_1} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{{3a}}{2};\,\,{p_2} = \frac{{3a}}{4} = \frac{{3a}}{{{2^2}}};...;{p_n} = \frac{{3a}}{{{2^n}}}\) (chứng minh bằng qui nạp)

Vì \(\lim \frac{1}{{{2^n}}} = \lim {\left( {\frac{1}{2}} \right)^n} = 0\) nên \(\lim {p_n} = 0\).

Ta có:

Diện tích tam giác ABC là \(S = \frac{{{a^2}\sqrt 3 }}{4}\)

Diện tích tam giác A₁B₁C₁ là \({S_1} = \frac{S}{4}\)

Bằng phương pháp qui nạp, ta chứng minh được rằng diện tích tam giác A_nB_nC_n là \({S_n} = \frac{{{a^2}\sqrt 3 }}{4}.{\left( {\frac{1}{4}} \right)^n}\)

Vì \(\lim {\left( {\frac{1}{4}} \right)^n} = 0\) nên \(\lim {S_n} = 0\).

Câu b:

Ta có (p_n) là cấp số nhân lùi vô hạn có công bội \(q = \frac{1}{2}\), do đó:

\({p_1} + {p_2} + ... + {p_n} + ... = \frac{{{p_1}}}{{1 - \frac{1}{2}}} = 2{p_1} = 3a\)

(S_n) là cấp số nhân lùi vô hạn có công bội \(q' = \frac{1}{4}\) do đó:

\({S_1} + {S_2} + ... + {S_n} + ... = \frac{{{S_1}}}{{1 - \frac{1}{4}}} = \frac{4}{3}{S_1} = \frac{S}{3} = \frac{{{a^2}\sqrt 3 }}{{12}}\)

---

Biểu diễn các số thập phân vô hạn tuần hoàn sau dưới dạng phân số:

a) 0,444...

b) 0,2121...

c) 0,32111...

Hướng dẫn giải:

Câu a:

\(\begin{array}{l}
0,444... = 0,4 + 0,04 + 0,004 + ...\\
 = \frac{4}{{10}} + \frac{4}{{{{10}^2}}} + \frac{4}{{{{10}^3}}} + ...\\
 = 4\left( {\frac{1}{{10}} + \frac{1}{{{{10}^2}}} + \frac{1}{{{{10}^3}}} + ...} \right)\\
 = 4.\frac{{\frac{1}{{10}}}}{{1 - \frac{1}{{10}}}} = \frac{4}{9}
\end{array}\)

Câu b:

\(\begin{array}{l}
0,2121 = 0,21 + 0,0021 + ... = \frac{{21}}{{{{10}^2}}} + \frac{{21}}{{{{10}^4}}} + ...\\
 = 21.\left( {\frac{1}{{{{10}^2}}} + \frac{1}{{{{10}^4}}} + ...} \right)\\
 = 21.\frac{{\frac{1}{{{{10}^2}}}}}{{1 - \frac{1}{{{{10}^2}}}}} = \frac{{21}}{{90}} = \frac{7}{{33}}
\end{array}\)

Câu c:

\(\begin{array}{l}
0,32111... = \frac{{32}}{{100}} + \frac{1}{{1000}} + \frac{1}{{1000}}.\frac{1}{{10}} + \frac{1}{{1000}}.{\left( {\frac{1}{{10}}} \right)^2} + ...\\
 = \frac{{32}}{{100}} + \frac{1}{{1000}}.\frac{1}{{1 - \frac{1}{{10}}}} = \frac{{32}}{{100}} + \frac{1}{{900}} = \frac{{289}}{{900}}
\end{array}\)

---

Gọi C là nửa đường tròn đường kính AB = 2R, C₁ là đường gồm hai nửa đường tròn đường kính \(\frac{{AB}}{2}\), C₂ là đường gồm bốn nửa đường tròn đường kính \(\frac{{AB}}{4}\),... C­_n là đường gồm 2n nửa đường tròn đường kính \(\frac{{AB}}{{2n}}\),... (h. 4.2). Gọi p_n là độ dài của C_n, S_n là diện tích hình  phẳng giới hạn bởi C­n và đoạn thẳng AB.

a. Tính p_n và S_n.

b. Tìm giới hạn của các dãy số (p_n) và (S_­n).

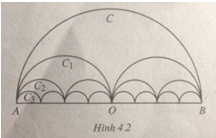
Hướng dẫn giải:

Câu a:

Ta có \({p_n} = {2^n}.\frac{R}{{{2^n}}}.\pi  = \pi R\) với mọi n

\({S_n} = {2^n}.{\left( {\frac{R}{{{2^n}}}} \right)^2}.\frac{\pi }{2} = \frac{{\pi {R^2}}}{2}.\frac{1}{{{2^n}}}\)

Câu b:

Ta có \(\lim {p_n} = \pi R;\lim {S_n} = 0\)

 

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 11 Chương 4 Bài 2 Dãy số có giới hạn hữu hạn với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 11 học tập thật tốt.