Bài 7 trang 16 SGK Toán 11 nâng cao
Xét tính chẵn – lẻ của mỗi hàm số sau:
a.
b. y = tan|x|
c. y = tanx−sin2x
Hướng dẫn giải:
Câu a:
Ta có
Vì
Nên
Câu b:
Tập xác định:
Do đó y = tan|x| là hàm số chẵn.
Câu c:
Tập xác định:
Do đó y = tanx–sin2x là hàm số lẻ.
Bài 8 trang 16 SGK Toán 11 nâng cao
Cho các hàm số sau:
a. y = −sin2x
b. y = 3tan2x+1
c. y = sinxcosx
d.
Chứng minh rằng mỗi hàm số y = f(x) đó đều có tính chất :
f(x+kπ) = f(x) với k ∈ Z, x thuộc tập xác định của hàm số f.
Hướng dẫn giải:
Với k ∈ Z ta có :
Câu a:
f(x) = −sin2x
f(x+kπ) = −sin2(x+kπ) = −[(−1)ksinx]2 = −sin2x = f(x)
Câu b:
f(x) = 3tan2x+1
f(x+kπ) = 3tan2(x+kπ)+1 = 3tan2x+1 = f(x)
Câu c:
f(x) = sinxcosx
f(x+kπ) = sin(x+kπ).cos(x+kπ) = (−1)ksinx.(−1)kcosx = sinxcosx = f(x)
Câu d:
Bài 9 trang 17 SGK Toán 11 nâng cao
Cho hàm số y = f(x) = Asin(ωx+∝) (A, ωvà ∝ là những hằng số; A và ω khác 0). Chứng minh rằng với mỗi số nguyên k), ta có f(x+k.2πω) = f(x) với mọi x.
Hướng dẫn giải:
Với k ∈ Z ta có:
Bài 10 trang 17 SGK Toán 11 nâng cao
Chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình
Hướng dẫn giải:
Đường thẳng

Chỉ có đoạn thẳng EF của đường thẳng đó nằm trong dải {(x;y)|−1 ≤ y ≤ 1} (dải này chứa đồ thị của hàm số y = sinx). Vậy các giao điểm của đường thẳng
Bài 11 trang 17 SGK Toán 11 nâng cao
Từ đồ thị của hàm số y = sinx, hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó:
a. y = −sinx
b. y = |sinx|
c. y = sin|x|
Hướng dẫn giải:
Câu a:
Đồ thị của hàm số y = −sinx là hình đối xứng qua trục hoành của đồ thị hàm số y = sinx
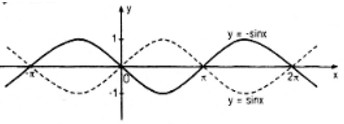
Câu b:
Ta có
do đó đồ thị của hàm số y = |sinx| có được từ đồ thị (C) của hàm số y = sinx bằng cách:
- Giữ nguyên phần đồ thị của (C) nằm trong nửa mặt phẳng y ≥ 0 (tức nửa mặt phẳng bên trên trục hoành kể cả bờ Ox).
- Lấy hình đối xứng qua trục hoành của phần đồ thị (C) nằm trong nửa mặt phẳng y < 0 (tức là nửa mặt phẳng bên dưới trục hoành không kể bờ Ox);
- Xóa phần đồ thị của (C) nằm trong nửa mặt phẳng y < 0.
- Đồ thị y = |sinx| là đường liền nét trong hình dưới đây:
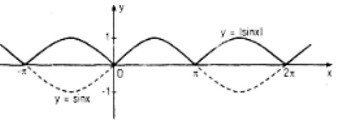
Câu c:
Ta có:
do đồ thị của hàm số y = sin|x| có được từ đồ thị (C) của hàm số y = sinx bằng cách :
- Giữ nguyên phần đồ thị của (C) nằm trong nửa mặt phẳng x ≥ 0 (tức nửa mặt phẳng bên phải trục tung kể cả bờ Oy).
- Xóa phần đồ thị của (C) nằm trong nửa mặt phẳng x < 0 (tức nửa mặt phẳng bên trái trục tung không kể bờ Oy).
- Lấy hình đối xứng qua trục tung của phần đồ thị (C) nằm trong nửa mặt phẳng x > 0
- Đồ thị y = sin|x| là đường nét liền trong hình dưới đây:
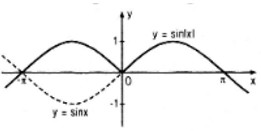
Bài 12 trang 17 SGK Toán 11 nâng cao
a. Từ đồ thị của hàm số y = cosx, hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó:
y = cosx+2
b. Hỏi mỗi hàm số đó có phải là hàm số tuần hoàn không ?
Hướng dẫn giải:
Câu a:
Đồ thị của hàm số y = cosx+2 có được do tịnh tiến đồ thị của hàm số y = cosx lên trên một đoạn có độ dài bằng 2, tức là tịnh tiến theo vectơ
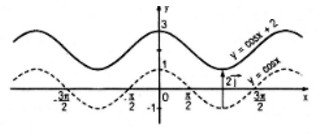
Đồ thị của hàm số
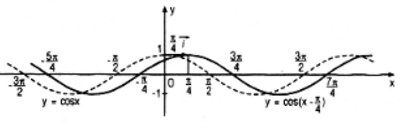
Câu b:
Các hàm số trên đều là hàm tuần hoàn vì:
Nếu f(x) = cosx+2 thì f(x+2π) = cos(x+2π)+2 = cosx+2 = f(x), ∀x ∈ R
Và nếu
Bài 13 trang 17 SGK Toán 11 nâng cao
Xét hàm số y = f(x) =
a. Chứng minh rằng với mỗi số nguyên k, f(x+k4π) = f(x) với mọi x.
b. Lập bảng biến thiên của hàm số y =
c. Vẽ đồ thị của các hàm số y = cosx và y =
d. Trong mặt phẳng tọa độ Oxy, xét phép biến hình F biến mỗi điểm (x;y) thành điểm (x′;y′) sao cho x′ = 2xvà y′ = y. Chứng minh rằng F biến đồ thị của hàm số y = cosx thành đồ thị của hàm số y =
Hướng dẫn giải:
Câu a:
Câu b:
Bảng biến thiên
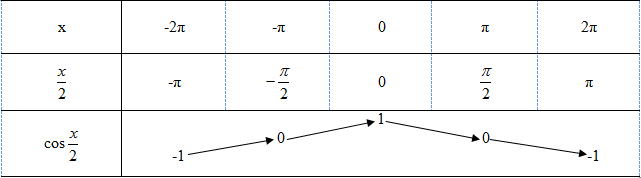
Câu c:
Đồ thị
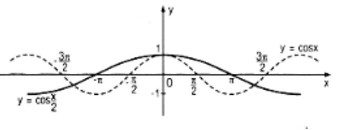
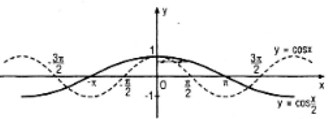
Câu d:
Nếu đặt x′ = 2x, y′ = y thì y = cosx khi và chỉ khi
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 11 Chương 1 Luyện tập (trang 16, 17) với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 11 học tập thật tốt.






Thảo luận về Bài viết