Giải Toán 11 SGK nâng cao Ôn tập Chương 1 Phép dời hình và đồng dạng trong mặt phẳng

Cho hai đường tròn (O ; R), (O’ ; R’) và một đường thẳng d

a. Tìm hai điểm M, N lần lượt nằm trên hai đường tròn đó sao cho d là đường trung trực của đoạn thẳng MN

b. Xác định điểm I trên d sao cho tiếp tuyến IT của (O ; R) và tiếp tuyến IT’ của (O’ ; R’) hợp thành các góc mà d là một trong các đường phân giác của các góc đó

Hướng dẫn giải:

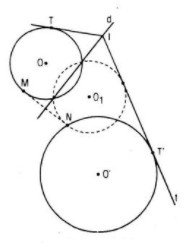
Câu a:

Gọi (O₁ ; R) là ảnh của đường tròn (O ; R) qua phép đối xứng trục Đ_d

Giao điểm (nếu có) của hai đường tròn (O₁ ; R) và (O’ ; R’) chính là điểm N cần tìm, điểm M là điểm đối xứng với N qua d

Câu b:

Vẫn gọi (O₁ ; R) như trên và I là điểm cần tìm thì IT’ là tiếp tuyến chung của hai đường tròn (O₁ ; R) và (O’ ; R’)

Suy ra cách dựng: Vẽ tiếp tuyến chung t (nếu có) của hai đường tròn (O₁ ; R) và (O’ ; R’)

Giao điểm (nếu có) của t và d chính là điểm I cần tìm

Khi đó tiếp tuyến IT’ chính là t còn đường thẳng đối xứng với IT’ qua d là tiếp tuyến IT của (O ; R)

---

Chứng minh rằng nếu một hình nào đó có hai trục đối xứng vuông góc với nhau thì hình đó có tâm đối xứng

Hướng dẫn giải:

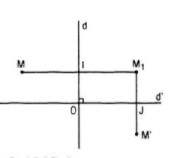
Giả sử hình H có hai trục đối xứng d và d’ vuông góc với nhau

Gọi O là giao điểm của hai trục đối xứng đó

Lấy M là điểm bất kì thuộc hình H, M₁ là điểm đối xứng với M qua d, M’ là điểm đối xứng với M₁ qua d’

Vì d và d’ đều là trục đối xứng của hình H nên M₁ và M’ đều thuộc H

Gọi I là trung điểm của MM₁, J là trung điểm của M₁M’ thì ta có:

\(\overrightarrow {OM}  = \overrightarrow {OI}  + \overrightarrow {IM}  = \overrightarrow {M'J}  + \overrightarrow {JO}  = \overrightarrow {M'O} \,\,hay\,\,\overrightarrow {OM}  + \overrightarrow {OM'}  = \overrightarrow 0 \)

Vậy phép đối xứng tâm O biến điểm M thuộc hình H thành điểm M’ thuộc H, suy ra H có tâm đối xứng là O

---

Cho đường thẳng d đi qua hai điểm phân biệt P, Q và hai điểm A, B nằm về một phía đối với d. Hãy xác định trên d hai điểm M, N sao cho \(\overrightarrow {MN}  = \overrightarrow {PQ} \)  và AM + BN bé nhất

Hướng dẫn giải:

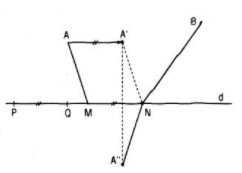
Giả sử hai điểm M, N nằm trên d sao cho \(\overrightarrow {MN}  = \overrightarrow {PQ} \)

Lấy điểm A’ sao cho \(\overrightarrow {AA'}  = \overrightarrow {PQ} \)  thì điểm A’ hoàn toàn xác định và AMNA’ là hình bình hành nên AM = A’N

Ta có: AM + BN = A’N + BN

Gọi A” là điểm đối xứng của A’ qua d, khi đó:

A’N + BN = A”N + BN ≥ A”B

Từ đó ta suy ra AM + BN nhỏ nhất khi N là giao điểm của BA” với d

Từ đó tìm được điểm M thỏa \(\overrightarrow {MN}  = \overrightarrow {AA'}  = \overrightarrow {PQ} \)

---

Cho vecto \({\vec u}\) và điểm O. Với điểm M bất kì, ta gọi M1là điểm đối xứng với M qua O và M’ là điểm sao cho \(\overrightarrow {{M_1}M}  = \vec u\). Gọi F là phép biến hình biến M thành M’

a. F là phép hợp thành của hai phép nào ? F có phải là phép dời hình hay không ?

b. Chứng tỏ rằng F là một phép đối xứng tâm

Hướng dẫn giải:

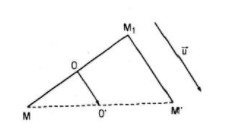
Câu a:

F là hợp thành của hai phép: phép đối xứng tâm Đ_O với tâm O và phép tịnh tiến T theo vecto \({\vec u}\). Ta có F là phép dời hình vì Đ_O và T là phép dời hình

Câu b:

Giả sử M₁ = Đ_O(M) và M’ = T(M₁)

Nếu gọi O’ là trung điểm của MM’ thì:

\(\overrightarrow {OO'}  = \frac{{\overrightarrow {{M_1}M'} }}{2} = \frac{{\overrightarrow u }}{2}\)

Vậy điểm O’ cố định và F chính là phép đối xứng qua tâm O’

---

Cho tam giác ABC nội tiếp trong đường tròn (O) và một điểm M thay đổi trên (O). Gọi M₁ là điểm đối xứng với M qua A, M₂ là điểm đối xứng với M₁ qua B, M₃ là điểm đối xứng với M₂ qua C

a. Chứng tỏ rằng phép biến hình F biến điểm M thành M3 là một phép đối xứng tâm

b. Tìm quỹ tích điểm M₃

Hướng dẫn giải:

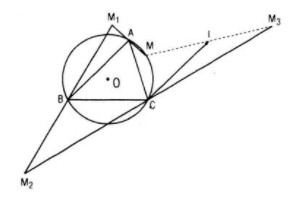
Câu a:

 Gọi I là trung điểm của MM₃, ta chứng minh I là điểm cố định

Thật vậy, ta có:

\(\begin{array}{l}
\overrightarrow {CI}  = \frac{1}{2}(\overrightarrow {CM}  + \overrightarrow {C{M_3}} )\\
 = \frac{1}{2}(\overrightarrow {CM}  + \overrightarrow {{M_2}C} )\\
 = \frac{1}{2}\overrightarrow {{M_2}M}  = \overrightarrow {BA} 
\end{array}\)

Vậy điểm I cố định, do đó phép biến hình F biến M thành M₃ là phép đối xứng qua điểm I

Câu b:

Quỹ tích điểm M₃ là đường tròn (O’), ảnh của đường tròn (O) qua phép đối xứng tâm với tâm I

---

Gọi F là phép biến hình có tính chất sau đây: Với mọi cặp điểm M, N và ảnh M’, N’ của chúng, ta luôn có \(\overrightarrow {M'N'}  = k\overrightarrow {MN} \) , trong đó k là một số không đổi khác 0. Hãy chứng minh rằng F là phép tịnh tiến hoặc phép vị tự

Hướng dẫn giải:

 

Ta lấy một điểm A cố định và đặt A’ = F(A)

Theo giả thiết, với điểm M bất kì và ảnh M’ =F(M) của nó, ta có \(\overrightarrow {A'M}  = k\overrightarrow {AM} \)

Nếu k = 1, thì \(\overrightarrow {A'M}  = \overrightarrow {AM} \), do đó \(\overrightarrow {MM'}  = \overrightarrow {AA'} \) ,và F là phép tịnh tiến theo vecto \(\overrightarrow {AA'} \)

Nếu k ≠ 1 thì có điểm O sao cho: \(\overrightarrow {OA'}  = k\overrightarrow {OA} \) (với O thỏa\(\overrightarrow {OA'}  = \frac{1}{{1 - k}}\overrightarrow {AA'} \))

Khi đó ta có:

\(\overrightarrow {OM'}  = \overrightarrow {OA'}  + \overrightarrow {A'M'}  = k\overrightarrow {OA}  + k\overrightarrow {AM}  = k\overrightarrow {OM} \)

Vậy F là phép vị tự tâm O, tỉ số k

---

a. Cho tam giác ABC và hình vuông MNPQ như hình 27. Gọi V là phép vị tự tâm A tỉ số \(k = \frac{{AB}}{{AM}}\) . Hãy dựng ảnh của hình vuông  MNPQ qua phép vị tự V

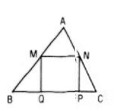
b. Từ bài toán ở câu a) hãy suy ra cách giải bài toán sau: Cho tamn giác nhọn ABC, hãy dựng hình vuông MNPQ sao cho hai đỉnh P, Q nằm trên cạnh BC và hai đỉnh M, N lần lượt nằm trên hai cạnh AB và AC

Hướng dẫn giải:

Câu a:

Ta có \(\overrightarrow {AB}  = k\overrightarrow {AM} ;\overrightarrow {AC}  = k\overrightarrow {AN} \) nên phép vị tự V biến điểm M thành điểm B, biến điểm N thành điểm C

Vậy V biến hình vuông MNPQ thành hình vuông BCP’Q’ như trên hình bên

Câu b:

Dựng hình vuông BCP’Q’ nằm ngoài tam giác ABC như hình

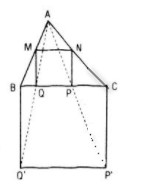
Lấy giao điểm P, Q của BC với các đoạn thẳng tương ứng AP’ và AQ’

Từ P và Q, kẻ các đường thẳng vuông góc với BC, lần lượt cắt AC và AB tại N và M

Khi đó MNPQ chính là hình vuông cần dựng

---

Cho đường tròn (O) có đường kính AB. Gọi C là điểm đối xứng với A và B và PQ là đường kính thay đổi của (O) khác đường kính AB. Đường thẳng CQ cắt PA và PB lần lượt tại M và N

a. Chứng minh rằng Q là trung điểm của CM, N là trung điểm của CQ.

b. Tìm quỹ tích các điểm M và N khi đường kính PQ thay đổi

Hướng dẫn giải:

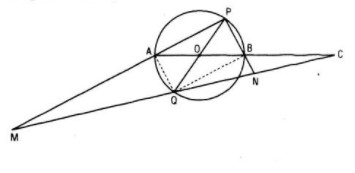
Câu a:

Ta có QB // AP (vì cùng vuông góc với PB) và B là trung điểm của AC nên Q là trung điểm của CM

Ta có AQ // BN (vì cùng vuông góc với AP) và B là trung điểm của AC nên N là trung điểm của CQ

Câu b:

Theo câu a) ta có \(\overrightarrow {CM}  = 2\overrightarrow {CQ} \) nên phép vị tự V tâm C tỉ số biến  Q thành M

Vì Q chạy trên đường tròn (O) (trừ hai điểm A, B) nên quỹ tích M là ảnh của đường tròn đó qua phép vị tự V (trừ ảnh của A, B)

Tương tự, ta có \(\overrightarrow {CN}  = \frac{1}{2}\overrightarrow {CQ} \) nên quỹ tích N là ảnh của đường tròn (O) qua phép vị tự V tâm C, tỉ số 1/2 (trừ ảnh của A, B)

---

Cho đường tròn (O ; R) và điểm A cố định Một dãy cung BC thay đổi của (O ; R) có độ dài không đổi BC = m. Tìm quỹ tích các điểm G sao cho \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

Hướng dẫn giải:

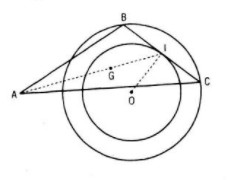
Gọi I là trung điểm của BC

\(\begin{array}{l}
\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \\
 \Leftrightarrow \overrightarrow {GA}  + 2\overrightarrow {GI}  = \overrightarrow 0 \\
 \Leftrightarrow \overrightarrow {AG}  = \frac{2}{3}\overrightarrow {AI} 
\end{array}\)

Tức là phép vị tự V tâm A tỉ số 2/3 biến điểm I thành điểm G

Trong tam giác vuông OIB ta có:

\(OI = \sqrt {O{B^2} - I{B^2}}  = \sqrt {{R^2} - {{\left( {\frac{m}{2}} \right)}^2}}  = R'\) (không đổi)

Nên quỹ tích I là đường tròn (O ; R’) hoặc là điểm O (nếu m = 2R)

Do đó quỹ tích G là ảnh của quỹ tích I qua phép vị tự V

 

 

Trên đây là nội dung hướng dẫn giải chi tiết bài tập SGK nâng cao môn Hình học 11 Ôn tập Chương 1 được trình bày rõ ràng, cụ thể với phương pháp ngắn gọn và khoa học. Hy vọng rằng đây sẽ là tài liệu hữu ích giúp các em học sinh lớp 11 học tập thật tốt!