Giải Toán 11 SGK nâng cao Ôn tập Chương 1 Hàm số lượng giác và phương trình lượng giác

Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?

a. Các hàm số y = sinx, y = cosx có cùng tập xác định.

b. Các hàm số y = tanx, y = cotx có cùng tập xác định.

c. Các hàm số y = sinx, y = tanx là những hàm số lẻ.

d. Các hàm số y = cosx, y = cotx là những hàm số chẵn.

e. Các hàm số y = sinx, y = cosx cùng nghịch biến trên khoảng $\left(\frac{\pi }{2};\frac{3\pi }{2}\right)$

f. Hàm số y = cosx nghịch biến trên khoảng $\left(-2\pi ;-\pi \right)$

g. Trên mỗi khoảng mà hàm số y = tanx đồng biến thì hàm số y = cotx nghịch biến.

Hướng dẫn giải:

Câu a:

Đúng vì hàm số y = sinx, y = cosx có cùng tập xác định D = R

Câu b:

Sai vì y = tanx xác định $\mathrm{\forall }x\ne \frac{\pi }{2}+k\pi$ còn y = cotx xác định ∀x ≠ kπ

Câu c:

Đúng

Câu d:

Sai vì y = cotx là hàm số lẻ.

Câu e:

Sai vì y = cosx không nghịch biến trên khoảng $\left(\frac{\pi }{2};\frac{3\pi }{2}\right)$

Câu f:

Đúng

Câu g:

Sai vì trên khoảng $\left(-2\pi ;-\pi \right)$ hàm số y = tanx đồng biến nhưng hàm số y = cotx không nghịch biến.

---

Xét hàm số y = f(x) = sinπx.

a. Chứng minh rằng với mỗi số nguyên chẵn m ta có f(x+m) = f(x) với mọi x.

b. Lập bảng biến thiên của hàm số trên đoạn [−1;1].

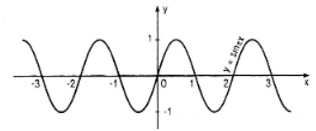
c. Vẽ đồ thị của hàm số đó.

Hướng dẫn giải:

Câu a:

Đặt m = 2k, k ∈ Z. Ta có:

f(x+m) = sinπ(x+m) = sin(πx+2kπ) = sinπx = f(x)

Câu b:

Bảng biến thiên

Câu c:

Đồ thị

---

Đưa các biểu thức về dạng $C\sin \left(x+\alpha \right)$:

a) $\sin x+\tan \frac{\pi }{7}\cos x$

b) $\tan \frac{\pi }{7}\sin x+\cos x$

Hướng dẫn giải:

Câu a:

$\begin{array}{l}\sin x+\tan \frac{\pi }{7}\cos x=\sin x+\frac{\sin \frac{\pi }{7}}{\cos \frac{\pi }{7}}\cos x\\ =\frac{1}{\cos \frac{\pi }{7}}\left(\sin x\cos \frac{\pi }{7}+\sin \frac{\pi }{7}\cos \frac{\pi }{7}\right)\\ =\frac{1}{\cos \frac{\pi }{7}}\sin \left(x+\frac{\pi }{7}\right)\end{array}$

Câu b:

$\begin{array}{l}\tan \frac{\pi }{7}\sin x+\cos x=\frac{\sin \frac{\pi }{7}}{\cos \frac{\pi }{7}}\sin x+\cos x\\ =\frac{1}{\cos \frac{\pi }{7}}\left(\sin x\sin \frac{\pi }{7}+\cos x\cos \frac{\pi }{7}\right)\\ =\frac{1}{\cos \frac{\pi }{7}}\cos \left(x-\frac{\pi }{7}\right)=\frac{1}{\cos \frac{\pi }{7}}\sin \left(x-\frac{\pi }{7}+\frac{\pi }{2}\right)\end{array}$

---

Giải các phương trình sau:

a) $\sin \left(x-\frac{2\pi }{3}\right)=\cos 2x$

b) $\tan \left(2x+{45}^0\right)\tan \left({180}^0-\frac{x}{2}\right)=1$

c) $\cos 2x-{\sin }^{2}x=0$

d) $5\tan x-2\cot x=3$

Hướng dẫn giải:

Câu a:

$\begin{array}{l}\sin \left(x-\frac{2\pi }{3}\right)=\cos 2x\\ \iff \sin \left(x-\frac{2\pi }{3}\right)=\sin \left(\frac{\pi }{2}-2x\right)\\ \iff [\begin{array}{c}x-\frac{2\pi }{3}=\frac{\pi }{2}-2x+k2\pi \\ x-\frac{2\pi }{3}=\pi -\frac{\pi }{2}+2x+k2\pi \end{array}\\ \iff [\begin{array}{c}x=\frac{7\pi }{8}+k\frac{2\pi }{3}\\ x=-\frac{7\pi }{6}-k2\pi \end{array}\end{array}$

Câu b:

Với ĐKXĐ của phương trình ta có tan(2x+45⁰) = cot(45⁰−2x) và $\tan \left({180}^0-\frac{x}{2}\right)=\tan \left(-\frac{x}{2}\right)$ nên:

$\begin{array}{l}\tan \left(2x+{45}^0\right)\tan \left({180}^0-\frac{x}{2}\right)=1\\ \iff \cot \left({45}^0-2x\right)\tan \left(-\frac{x}{2}\right)=1\\ \iff \tan \left(-\frac{x}{2}\right)=\tan \left({45}^0-2x\right)\\ \iff -\frac{x}{2}={45}^0-2x+k{180}^0\\ \iff x={30}^0+k{120}^0,k\in Z\end{array}$

Câu c:

$\begin{array}{l}\cos 2x-{\sin }^{2}x=0\\ \iff \cos 2x-\frac{1-\cos 2x}{2}=0\\ \iff 3\cos 2x-1=0\\ \iff \cos 2x=\frac{1}{3}\\ \iff \cos 2x=\cos \alpha \left(\cos \alpha =\frac{1}{3}\right)\\ \iff x=\pm \frac{\alpha }{2}+k\pi \left(k\in Z\right)\end{array}$

Câu d:

$\begin{array}{l}5\tan x-2\cot x=3\\ \iff 5\tan x-\frac{2}{\tan x}=3\\ \iff 3{\tan }^{2}x-3\tan x-2=0\\ \iff [\begin{array}{c}\tan x=1\\ \tan x=-\frac{2}{5}\end{array}\iff [\begin{array}{c}x=\frac{\pi }{4}+k\pi \\ x=\alpha +k\pi \end{array}\left(k\in Z\right)\end{array}$

trong đó $\tan \alpha =-\frac{2}{5}$.

---

Giải các phương trình sau:

a.  $\sin 2x+{\sin }^{2}x=\frac{1}{2}$

b.  2sin²x+3sinxcosx+cos²x = 0

c.  ${\sin }^2\frac{x}{2}+\sin x-2{\cos }^2\frac{x}{2}=\frac{1}{2}$

Hướng dẫn giải:

Câu a:

Ta có:

$\begin{array}{l}\sin 2x+{\sin }^{2}x=\frac{1}{2}\\ \iff \sin 2x+\frac{1}{2}\left(1-\cos 2x\right)=\frac{1}{2}\\ \iff \sin 2x-\frac{1}{2}\cos 2x=0\\ \iff \tan 2x=\frac{1}{2}\end{array}$

$\iff 2x=\alpha +k\pi$ với $\tan \alpha =\frac{1}{2}$

$\iff x=\frac{\alpha }{2}+k\frac{\pi }{2},k\in Z$

Câu b:

$x=\frac{\pi }{2}+k\pi$ không là nghiệm phương trình.

Chia hai vế phương trình cho cos²x ta được:

$\begin{array}{l}2{\tan }^{2}x+3\tan x+1=0\iff [\begin{array}{c}\tan x=-1\\ \tan x=-\frac{1}{2}\end{array}\\ \iff [\begin{array}{c}x=-\frac{\pi }{4}+k\pi \\ x=\alpha +k\pi \end{array}\left(k\in Z\right)\end{array}$

(với $\tan \alpha =-\frac{1}{2}$)

Câu c:

Ta có:

$\begin{array}{l}{\sin }^2\frac{x}{2}+\sin x-2{\cos }^2\frac{x}{2}=\frac{1}{2}\\ \iff {\sin }^2\frac{x}{2}+2\sin \frac{x}{2}\cos \frac{x}{2}-2{\cos }^2\frac{x}{2}=\frac{1}{2}\end{array}$

Với x mà $\cos \frac{x}{2}=0$ không là nghiệm phương trình.

Chia hai vế phương trình cho cos²x2 ta được:

$\begin{array}{l}{\tan }^2\frac{x}{2}+2\tan \frac{x}{2}-2=\frac{1}{2}\left(1+{\tan }^2\frac{x}{2}\right)\\ \iff {\tan }^2\frac{x}{2}+4\tan \frac{x}{2}-5=0\end{array}$

$\iff [\begin{array}{l}\tan \frac{x}{2}=1\\ \tan \frac{x}{2}=-5\end{array}\iff [\begin{array}{l}\frac{x}{2}=\frac{\pi }{4}+k\pi \\ \frac{x}{2}=\alpha +k\pi \end{array}$ với $\tan \alpha =-5$

$\iff [\begin{array}{l}x=\frac{\pi }{2}+k2\pi \\ x=2\alpha +k2\pi \end{array}\left(k\in Z\right)$

---

a. Chứng minh rằng $\sin \frac{\pi }{12}=\frac{\sqrt{3}-1}{2\sqrt{2}}$

b. Giải các phương trình $2\sin x-2\cos x=1-\sqrt{3}$ bằng cách biến đổi vế trái về dạng Csin(x+α)

c. Giải phương trình $2\sin x-2\cos x=1-\sqrt{3}$ bằng cách bình phương hai vế.

Hướng dẫn giải:

Câu a:

Ta có:

$\begin{array}{l}\sin \frac{\pi }{12}=\sin \left(\frac{\pi }{3}-\frac{\pi }{4}\right)\\ =\sin \frac{\pi }{3}\cos \frac{\pi }{4}-\sin \frac{\pi }{4}\cos \frac{\pi }{3}\\ =\frac{\sqrt{3}}{2}.\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}.\frac{1}{2}\\ =\frac{\sqrt{6}-\sqrt{2}}{4}=\frac{\sqrt{2}\left(\sqrt{3}-1\right)}{4}=\frac{\sqrt{3}-1}{2\sqrt{2}}\end{array}$

Câu b:

Ta có:

$\begin{array}{l}2\sin x-2\cos x=1-\sqrt{3}\\ \iff \frac{1}{\sqrt{2}}\sin x-\frac{1}{\sqrt{2}}\cos x=\frac{1-\sqrt{3}}{2\sqrt{2}}\\ \iff \sin x.\cos \frac{\pi }{4}-\sin \frac{\pi }{4}\cos x=-\sin \frac{\pi }{12}\\ \iff \sin \left(x-\frac{\pi }{4}\right)=\sin \left(-\frac{\pi }{12}\right)\\ \iff [\begin{array}{c}x-\frac{\pi }{4}=-\frac{\pi }{12}+k2\pi \\ x-\frac{\pi }{4}=\pi +\frac{\pi }{12}+k2\pi \end{array}\\ \iff [\begin{array}{c}x=\frac{\pi }{6}+k2\pi \\ x=\frac{4\pi }{3}+k2\pi \end{array}\left(k\in Z\right)\end{array}$

Câu c:

Chú ý rằng $1-\sqrt{3}<0$, ta đặt điều kiện sinx–cosx < 0 rồi bình phương hai vế của phương trình thì được:

$\begin{array}{l}4\left(1-\sin 2x\right)=4-2\sqrt{3}\\ \iff \sin 2x=\frac{\sqrt{3}}{2}\iff [\begin{array}{c}x=\frac{\pi }{6}+k\pi \\ x=\frac{\pi }{3}+k\pi \end{array}\left(k\in Z\right)\end{array}$

Thử vào điều kiện sinx–cosx < 0, ta thấy:

• Họ nghiệm $x=\frac{\pi }{6}+k\pi$ thỏa mãn điều kiện sinx–cosx < 0 khi và chỉ khi k chẵn, tức là $x=\frac{\pi }{6}+2m\pi ,m\in Z$.
• Họ nghiệm $x=\frac{\pi }{3}+k\pi$ thỏa mãn điều kiện sinx–cosx < 0 khi và chỉ khi k lẻ, tức là $x=\frac{\pi }{3}+k\pi$.

Ta có kết quả như đã nêu ở câu b. 

---

Giải phương trình:

$\frac{1+\cos 2x}{\cos x}=\frac{\sin 2x}{1-\cos 2x}$

Hướng dẫn giải:

ĐKXĐ: $\cos x\ne 0$ và $\cos 2x\ne 1$. Với điều kiện đó, ta có:

$\begin{array}{l}\frac{1+\cos 2x}{\cos x}=\frac{\sin 2x}{1-\cos 2x}\\ \iff \frac{2{\cos }^{2}x}{\cos x}=\frac{2\sin x\cos x}{2{\sin }^{2}x}\\ \iff 1-\frac{1}{2\sin x}=0\\ \iff \sin x=\frac{1}{2}\iff [\begin{array}{c}x=\frac{\pi }{6}+k2\pi \left(n\right)\\ x=\frac{5\pi }{6}+k2\pi \left(n\right)\end{array}\left(k\in Z\right)\end{array}$

---

Cho phương trình $\frac{{\sin }^{3}x+{\cos }^{3}x}{2\cos x-\sin x}=\cos 2x$.

a. Chứng minh rằng $x=\frac{\pi }{2}+k\pi$ nghiệm đúng phương trình.

b. Giải phương trình bằng cách đặt tanx = t (khi $x\ne \frac{\pi }{2}+k\pi$)

Hướng dẫn giải:

Câu a:

Thay $x=\frac{\pi }{2}+k\pi$ vào phương trình ta được:

$\frac{{\left(-1\right)}^{3k}}{-{\left(-1\right)}^k}=\cos \pi \iff -1=-1$ (luôn đúng)

Vậy $x=\frac{\pi }{2}+k\pi$ là nghiệm phương trình

Câu b:

• $x=\frac{\pi }{2}+k\pi$ là nghiệm phương trình.
• Với $x\ne \frac{\pi }{2}+k\pi$ chia tử và mẫu của vế trái cho cos³x ta được:

$\frac{{\tan }^{3}x+1}{2\left(1+{\tan }^{2}x\right)-\tan x\left(1+{\tan }^{2}x\right)}=\frac{1-{\tan }^{2}x}{1+{\tan }^{2}x}$

Đặt t = tanx ta được:

$\begin{array}{l}\frac{t^3+1}{\left(2-t\right)\left(1+t^2\right)}=\frac{1-t^2}{1+t^2}\\ \iff t^3+1=\left(t^2-1\right)\left(t-2\right)\\ \iff t^3+1=t^3-2t^2-t+2\\ \iff 2t^2+t-1=0\\ \iff [\begin{array}{c}t=-1\\ t=\frac{1}{2}\end{array}\end{array}$

$\iff [\begin{array}{l}\tan x=-1\\ \tan x=\frac{1}{2}\end{array}\iff [\begin{array}{l}x=-\frac{\pi }{4}+k\pi \\ x=\alpha +k\pi \end{array}$

Vậy phương trình đã cho có nghiệm: $x=\frac{\pi }{2}+k\pi ,x=-\frac{\pi }{4}+k\pi ,x=\alpha +k\pi \left(k\in Z\right)$

 

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 11 Ôn tập Chương 1 Hàm số lượng giác và phương trình lượng giác với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 11 học tập thật tốt.