Bài 7 trang 95 SGK Hình học 11 nâng cao
Mỗi khẳng định sau có đúng không ?
a. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
b. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
Hướng dẫn giải:
Câu a:
Sai : lấy hai đường thẳng cắt nhau b, c nằm trong mp(P) và a vuông góc với (P).
Khi đó, a ⊥ b, a ⊥ c nhưng b, c cắt nhau.
Câu b:
Sai : lấy b // c, b, c ⊂ (P) và a ⊥ (P)
Bài 8 trang 95 SGK Hình học 11 nâng cao
a. Cho vecto \(\overrightarrow n \) khác \(\overrightarrow 0 \) và hai vecto \(\overrightarrow a \), \(\overrightarrow b \) không cùng phương. Chứng minh rằng nếu vecto \(\overrightarrow n \) vuông góc với cả hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) thì ba vecto \(\overrightarrow n \), \(\overrightarrow a \), \(\overrightarrow b \) không đồng phẳng.
b. Chứng minh rằng ba vecto cùng vuông góc với vecto \(\overrightarrow n \ne \overrightarrow 0 \) thì đồng phẳng. Từ đó suy ra các đường thẳng cùng vuông góc với một đường thẳng thì cùng song song với một mặt phẳng.
Hướng dẫn giải:
Câu a:
Nếu \(\overrightarrow n \), \(\overrightarrow a \), \(\overrightarrow b \) đồng phẳng thì có hai số k, l sao cho \(\overrightarrow n = k.\overrightarrow a + l.\overrightarrow b \)
\(\begin{array}{l}
\Rightarrow \overrightarrow n = k.\overrightarrow a + l.\overrightarrow b \\
\overrightarrow n .\overrightarrow n = k.\overrightarrow a .\overrightarrow n + l.\overrightarrow b .\overrightarrow n = 0 \Rightarrow |\overrightarrow n {|^2} = {\overrightarrow n ^2} = 0\\
\Rightarrow |\overrightarrow n | = 0
\end{array}\)
\( \Rightarrow \overrightarrow n = \overrightarrow 0 \) (vô lí)
Vậy \(\overrightarrow n \), \(\overrightarrow a \), \(\overrightarrow b \) không đồng phẳng
Câu b:
Giả sử ba vecto cùng vuông góc với \(\overrightarrow n \) là \(\overrightarrow n \), \(\overrightarrow a \), \(\overrightarrow b \)
Tức là \(\overrightarrow a .\overrightarrow n = \overrightarrow b .\overrightarrow n = \overrightarrow c .\overrightarrow n = 0\)
Nếu \(\overrightarrow a \) và \(\overrightarrow b \) là hai vecto cùng phương thì \(\overrightarrow a \), \(\overrightarrow b \)\(\overrightarrow c \) đồng phẳng
Nếu \(\overrightarrow a \)và \(\overrightarrow b \) là hai vecto không cùng phương thì \(\overrightarrow a \), \(\overrightarrow b \)\(\overrightarrow n \) là ba vecto không đồng phẳng (điều này suy ra từ câu a)
Bài 9 trang 96 SGK Hình học 11 nâng cao
Cho hình chóp S.ABC có SA = SB = SC và \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA}\). Chứng minh rằng SA ⊥ BC, SB ⊥ AC, SC ⊥ AB.
Hướng dẫn giải:
\(\begin{array}{*{20}{l}}
{\widehat {ASB} = \widehat {BSC} = \widehat {CSA}}\\
{\overrightarrow {SA} .\overrightarrow {BC} = \overrightarrow {SA} .(\overrightarrow {SC} - \overrightarrow {SB} )}\\
{ = \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SA} .\overrightarrow {SB} }\\
{ = SA.SC.\cos \widehat {ASC} - SA.SB.\cos \widehat {ASB} = 0}
\end{array}\)
=> SA ⊥ BC
Tương tự : SB ⊥ AC và SC ⊥ AB
Bài 10 trang 96 SGK Hình học 11 nâng cao
Cho hình tứ diện ABCD. Chứng minh rằng nếu \(\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AD} .\overrightarrow {AB} \) thì AB ⊥ CD, AC ⊥ BD, AD ⊥ BC. Điều ngược lại có đúng không ?
Hướng dẫn giải:
Ta có:
\(\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AC} .\overrightarrow {AD} \Leftrightarrow \overrightarrow {AC} .\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right) = 0\\
\Leftrightarrow \overrightarrow {AC} .\overrightarrow {BD} = 0 \Leftrightarrow AC \bot BD
\end{array}\)
Tương tự
\(\begin{array}{l}
\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AD} .\overrightarrow {AB} \Leftrightarrow AD \bot BC\\
\overrightarrow {AD} .\overrightarrow {AB} = \overrightarrow {AB} .\overrightarrow {AC} \Leftrightarrow AB \bot CD
\end{array}\)
Như vậy, điều ngược lại cũng đúng
Bài 11 trang 96 SGK Hình học 11 nâng cao
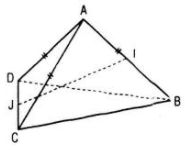
Cho hình tứ diện ABCD có AB = AC = AD và \(\widehat {BAC} = {60^0},\widehat {BAD} = {60^0}.\)
Chứng minh rằng :
a. AB ⊥ CD;
b. Nếu I và J lần lượt là trung điểm của AB và CD thì IJ ⊥ AB và IJ ⊥ CD.
Hướng dẫn giải:
Câu a:
Ta có:
\(\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} \left( {\overrightarrow {AD} - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \\
= AB.AD.cos\widehat {BAD} - AB.AC.cos\widehat {BAC} = 0\\
\Rightarrow AB \bot CD.
\end{array}\)
Câu b:
Ta có:
\(\begin{array}{l}
\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AJ} \\
= \frac{1}{2}\overrightarrow {BA} + \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {AC} } \right)\\
= \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)\\
= \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {AC} - \overrightarrow {AB} } \right)\\
\Rightarrow \overrightarrow {AB} .\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} - \overrightarrow {AC} - A{B^2}} \right)\\
= \frac{1}{2}(AB.AD.cos{60^0} + AB.AC.cos{60^0} - A{B^2}) = 0\\
\Rightarrow AB \bot IJ
\end{array}\)
Mặt khác:
\(\begin{array}{l}
\overrightarrow {CD} .\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {AD} } \right).\left( {\overrightarrow {AD} + \overrightarrow {BA} + \overrightarrow {AC} } \right)\\
= \frac{1}{2}\left( { - \overrightarrow {AC} .\overrightarrow {AD} + {{\overrightarrow {AD} }^2} + \overrightarrow {CA} .\overrightarrow {BA} + \overrightarrow {AD} .\overrightarrow {BA} - {{\overrightarrow {AC} }^2} + \overrightarrow {AD} .\overrightarrow {AC} } \right)\\
= - \frac{1}{2}\overrightarrow {AB} .\left( {\overrightarrow {CA} + \overrightarrow {AD} } \right) = - \frac{1}{2}\overrightarrow {AB} .\overrightarrow {CD} = 0\\
\Rightarrow CD \bot IJ
\end{array}\)
Trên đây là nội dung hướng dẫn giải chi tiết bài tập SGK nâng cao môn Hình học 11 Chương 3 Bài 2 Hai đường thẳng vuông góc được trình bày rõ ràng, cụ thể với phương pháp ngắn gọn và khoa học. Hy vọng rằng đây sẽ là tài liệu hữu ích giúp các em học sinh lớp 11 học tập thật tốt!
