Bài 1 trang 34 SGK Hình học 10 nâng cao
Cho tam giác ABCABC . Hãy xác định các vec tơ:
\(\begin{array}{l}
\overrightarrow {AB} + \overrightarrow {BC} ;\,\,\,\overrightarrow {CB} + \overrightarrow {BA} ;\,\,\overrightarrow {AB} + \overrightarrow {CA} ;\,\,\overrightarrow {BA} + \overrightarrow {CB} ;\\
\overrightarrow {BA} + \overrightarrow {CA} ;\,\,\overrightarrow {CB} - \overrightarrow {CA} ;\,\,\overrightarrow {AB} - \overrightarrow {CB} ;\,\,\overrightarrow {BC} - \overrightarrow {AB} .
\end{array}\)
Hướng dẫn giải:
Ta có:
\(\begin{array}{l}
\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \\
\overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA} \\
\overrightarrow {AB} + \overrightarrow {CA} = \overrightarrow {CA} + \overrightarrow {AB} = \overrightarrow {CB} \\
\overrightarrow {BA} + \overrightarrow {CB} = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA}
\end{array}\)
\(\overrightarrow {BA} + \overrightarrow {CA} = \overrightarrow {BA} + \overrightarrow {AD} = \overrightarrow {BD} \) (với D thỏa mãn \(\overrightarrow {CA} = \overrightarrow {AD} \) tức D là điểm đối xứng với C qua A).
\(\begin{array}{l}
\overrightarrow {CB} - \overrightarrow {CA} = \overrightarrow {AB} \\
\overrightarrow {AB} - \overrightarrow {CB} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC}
\end{array}\)
\(\overrightarrow {BC} - \overrightarrow {AB} = \overrightarrow {BC} + \overrightarrow {BA} = \overrightarrow {BE} \) (với E là điểm sao cho BCEA là hình bình hành).
Bài 2 trang 34 SGK Hình học 10 nâng cao
Cho ba điểm O, A, B không thẳng hàng. Tìm điều kiện cần và đủ để vec tơ \(\overrightarrow {OA} + \overrightarrow {OB} \) có giá là đường phân giác của góc AOB.
Hướng dẫn giải:
Gọi C là điểm sao cho AOBC là hình bình hành.
Ta có \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \)
OC là phân giác của góc AOB khi và chỉ khi AOBC là hình thoi.
⇔ OA = OB.
Bài 3 trang 34 SGK Hình học 10 nâng cao
Gọi O là tâm của hình bình hành ABCD. Chứng minh rằng với điểm M bất kì, ta có
\(\overrightarrow {MO} = \frac{1}{4}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right)\)
Hướng dẫn giải:
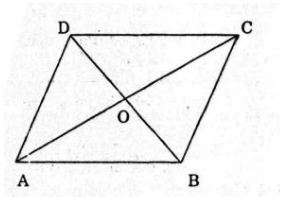
Do ABCD là hình bình hành nên O là trung điểm của AC, BD.
Suy ra \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 ,\,\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0 \)
Ta có:
\(\begin{array}{l}
\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \overrightarrow {MO} + \overrightarrow {OA} + \overrightarrow {MO} + \overrightarrow {OB} + \overrightarrow {MO} + \overrightarrow {OC} + \overrightarrow {MO} + \overrightarrow {OD} \\
= 4\overrightarrow {MO} + \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right) = 4\overrightarrow {MO} + \overrightarrow 0 + \overrightarrow 0 = 4\overrightarrow {MO} \\
\Rightarrow \overrightarrow {MO} = \frac{1}{4}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right)
\end{array}\)
Bài 4 trang 34 SGK Hình học 10 nâng cao
Cho tam giác ABC.
a) Tìm các điểm M và N sao cho
\(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \) và \(2\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \)
b) Với các điểm M, N ở câu a) , tìm các số p và q sao cho \(\overrightarrow {MN} = p\overrightarrow {AB} + q\overrightarrow {AC} \)
Hướng dẫn giải:
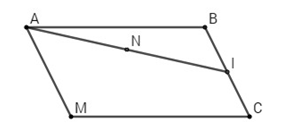
Câu a:
Ta có \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BA} + \overrightarrow {MC} = \overrightarrow 0 \)
⇔ \(\overrightarrow {CM} = \overrightarrow {BA} \). Do đó ABCM là hình bình hành.
Gọi I là trung điểm của BC, ta có \(\overrightarrow {NB} + \overrightarrow {NC} = 2\overrightarrow {NI} \) suy ra \(2\overrightarrow {NA} + 2\overrightarrow {NI} = \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {NA} + \overrightarrow {NI} = \overrightarrow 0 \Rightarrow \) N là trung điểm của AI.
Câu b:
Từ câu a), ta biểu diễn \(\overrightarrow {AM} ,\overrightarrow {AN} \) qua \(\overrightarrow {AB} ,\overrightarrow {AC} \).
\(\begin{array}{l}
\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow - \overrightarrow {AM} - \left( {\overrightarrow {AB} - \overrightarrow {AM} } \right) + \left( {\overrightarrow {AC} - \overrightarrow {AM} } \right) = \overrightarrow 0 \\
\Leftrightarrow \overrightarrow {AM} = - \overrightarrow {AB} + \overrightarrow {AC} \\
2\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \Leftrightarrow - 2\overrightarrow {AN} + \overrightarrow {AB} - \overrightarrow {AN} + \overrightarrow {AC} - \overrightarrow {AN} = \overrightarrow 0 \\
\Leftrightarrow 4\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AC} \Leftrightarrow \overrightarrow {AN} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\\
\Rightarrow \overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) + \overrightarrow {AB} - \overrightarrow {AC} = \frac{5}{4}\overrightarrow {AB} - \frac{3}{4}\overrightarrow {AC}
\end{array}\)
Vậy \(p = \frac{5}{4};q = - \frac{3}{4}\)
Bài 5 trang 35 SGK Hình học 10 nâng cao
Cho đoạn thẳng AB và điểm I sao cho \(2\overrightarrow {IA} + 3\overrightarrow {IB} = \overrightarrow 0 \)
a) Tìm số k sao cho \(\overrightarrow {IA} = k\overrightarrow {AB} \)
b) Chứng minh rằng với mọi điểm M ta có: \(\overrightarrow {MI} = \frac{2}{5}\overrightarrow {MA} + \frac{3}{5}\overrightarrow {MB} \)
Hướng dẫn giải:
Câu a:
Ta có:
\(\begin{array}{l}
2\overrightarrow {IA} + 3\overrightarrow {IB} = \overrightarrow 0 \Leftrightarrow - 2\overrightarrow {IA} + 3\left( {\overrightarrow {AB} - \overrightarrow {AI} } \right) = \overrightarrow 0 \\
\Leftrightarrow - 5\overrightarrow {AI} + 3\overrightarrow {AB} = 0\\
\Leftrightarrow \overrightarrow {AI} = \frac{3}{5}\overrightarrow {AB}
\end{array}\)
Vậy là giá trị cần tìm
Câu b:
Với M bất kì, ta có:
\(\begin{array}{l}
2\overrightarrow {IA} + 3\overrightarrow {IB} = \overrightarrow 0 \\
\Leftrightarrow 2\left( {\overrightarrow {MA} - \overrightarrow {MI} } \right) + 3\left( {\overrightarrow {MB} - \overrightarrow {MI} } \right) = \overrightarrow 0 \\
\Leftrightarrow - 5\overrightarrow {MI} + 2\overrightarrow {MA} + 3\overrightarrow {MB} = \overrightarrow 0 \\
\Leftrightarrow \overrightarrow {MI} = \frac{2}{5}\overrightarrow {MA} + \frac{3}{5}\overrightarrow {MB}
\end{array}\)
Bài 6 trang 35 SGK Hình học 10 nâng cao
Trong mặt phẳng tọa độ cho ba điểm A(- 1;3); B(4;2); C(3;5).
a) Chứng minh rằng ba điểm A. B, C không thẳng hàng.
b) Tìm tọa độ điểm D sao cho \(\overrightarrow {AD} = - 3\overrightarrow {BC} \).
c) Tìm tọa độ điểm E sao cho 0 là trọng tâm tam giác ABE.
Hướng dẫn giải:
Câu a:
Ta có \(\overrightarrow {AB} = \left( {5; - 1} \right);\overrightarrow {AC} = \left( {4;1} \right)\)
Suy ra không tồn tại số k nào để \(\overrightarrow {AB} = k\overrightarrow {AC} \) hay A, B, C không thẳng hàng.
Câu b:
Gọi D có tọa độ là (x;y)
\( \Rightarrow \overrightarrow {AD} = \left( {x + 1;y - 3} \right)\) mà \(\overrightarrow {BC} = \left( { - 1;3} \right)\)
Do đó \(\overrightarrow {AD} = - 3\overrightarrow {BC} \)
\( \Leftrightarrow \left\{ \begin{array}{l}
x + 1 = - 3\left( { - 1} \right)\\
y - 3 = - 3.3
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 2\\
y = - 6
\end{array} \right.\)
Vậy D(2;- 6)
Câu c:
Gọi E(xE;yE)
Vì O là trọng tâm của tam giác ABE nên ta có:
\(\left\{ \begin{array}{l}
\frac{{{x_A} + {x_B} + {x_E}}}{3} = 0\\
\frac{{{y_A} + {y_B} + {y_C}}}{3} = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
\frac{{ - 1 + 4 + {x_E}}}{3} = 0\\
\frac{{3 + 2 + {y_E}}}{3} = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x_E} = - 3\\
{y_E} = - 5
\end{array} \right.\)
Vậy E(- 3;- 5)
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Ôn tập Chương 1 Vectơ với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.
