Bài 14 trang 17 SGK Hình học 10 nâng cao
Trả lời các câu hỏi sau đây:
a) Vectơ đối của vectơ \(-\overrightarrow a \) là vectơ nào?
b) Vectơ đối của vectơ \(\overrightarrow 0 \) là vectơ nào?
c) Vectơ đối của vectơ \(\overrightarrow a + \overrightarrow b \) là vectơ nào?
Hướng dẫn giải:
Câu a:
Vectơ đối của vectơ \(-\overrightarrow a \) là vectơ \( - \left( { - \overrightarrow a } \right) = \overrightarrow a \)
Câu b:
Vectơ đối của vectơ \(\overrightarrow 0 \) là vectơ \(\overrightarrow 0 \).
Câu c:
Vectơ đối của vectơ \(\overrightarrow a + \overrightarrow b \) là vectơ \( - \overrightarrow a - \overrightarrow b \)
Bài 15 trang 17 SGK Hình học 10 nâng cao
Chứng minh các mệnh đề sau đây:
a) Nếu \(\overrightarrow a + \overrightarrow b = \overrightarrow c \) thì \(\overrightarrow a = \overrightarrow c - \overrightarrow b ,\overrightarrow b = \overrightarrow c - \overrightarrow a \)
b) \(\overrightarrow a - \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow a - \overrightarrow b - \overrightarrow c \)
c) \(\overrightarrow a - \left( {\overrightarrow b - \overrightarrow c } \right) = \overrightarrow a - \overrightarrow b + \overrightarrow c \)
Hướng dẫn giải:
Câu a:
Cộng hai vế cho vectơ đối của vectơ \(\overrightarrow b\) ta có
\(\overrightarrow a + \overrightarrow b + \left( { - \overrightarrow b } \right) = \overrightarrow c + \left( { - \overrightarrow b } \right) \Rightarrow \overrightarrow a = \overrightarrow c - \overrightarrow b \)
Cộng hai vế cho vectơ đối của vectơ \(\overrightarrow a\) ta có
\(\overrightarrow a + \overrightarrow b + \left( { - \overrightarrow a } \right) = \overrightarrow c + \left( { - \overrightarrow a } \right) \Rightarrow \overrightarrow b = \overrightarrow c - \overrightarrow a \)
Câu b:
Ta có \(\overrightarrow a - \left( {\overrightarrow b + \overrightarrow c } \right) + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow a \)
Áp dụng câu a) ta có \(\overrightarrow a - \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow a - \overrightarrow b - \overrightarrow c \)
Câu c:
Áp dụng câu a) ta có \(\overrightarrow a - \left( {\overrightarrow b - \overrightarrow c } \right) = \overrightarrow a - \left[ {\overrightarrow b + \left( { - \overrightarrow c } \right)} \right] = \overrightarrow a - \overrightarrow b - \left( { - \overrightarrow c } \right) = \overrightarrow a - \overrightarrow b + \overrightarrow c \)
Bài 16 trang 17 SGK Hình học 10 nâng cao
Cho hình bình hành ABCDvới tâm O. Mỗi khẳng định sau đây đúng hay sai ?
a) \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {AB} \)
b) \(\overrightarrow {CO} - \overrightarrow {OB} = \overrightarrow {BA} \)
c) \(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {AC} \)
d) \(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {BD} \)
e) \(\overrightarrow {CD} - \overrightarrow {CO} = \overrightarrow {BD} - \overrightarrow {BO} \)
Hướng dẫn giải:
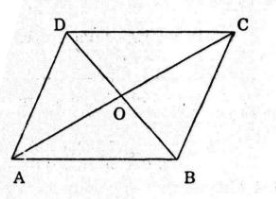
Câu a:
Sai vì \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \ne \overrightarrow {AB} \)
Câu b:
Đúng vì \(\overrightarrow {CO} - \overrightarrow {OB} = \overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \)
Câu c:
Sai vì \(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {BD} \ne \overrightarrow {AC} \)
Câu d:
Sai vì \(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \ne \overrightarrow {BD} \)
Câu e:
Đúng vì \(\overrightarrow {CD} - \overrightarrow {CO} = \overrightarrow {BD} - \overrightarrow {BO} = \overrightarrow {OD} \)
Bài 17 trang 17 SGK Hình học 10 nâng cao
Cho hai điểm A, B phân biệt.
a) Tìm tập hợp các điểm O sao cho \(\overrightarrow {OA} = \overrightarrow {OB} \);
b) Tìm tập hợp các điểm O sao cho \(\overrightarrow {OA} =-\overrightarrow {OB} \) .
Hướng dẫn giải:
Câu a:
\(\overrightarrow {OA} = \overrightarrow {OB} \) thì \(A \equiv B\) (vô lý do A, B) phân biệt).
Vậy tập hợp điểm O thỏa mãn \(\overrightarrow {OA} = \overrightarrow {OB} \) là tập rỗng.
Câu b:
Ta có \(\overrightarrow {OA} = - \overrightarrow {OB} \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow 0 \Leftrightarrow \) O là trung điểm đoạn AB.
Vậy tập hợp điểm O thỏa mãn \(\overrightarrow {OA} =-\overrightarrow {OB} \) chỉ có duy nhất một điểm là trung điểm của đoạn AB.
Bài 18 trang 17 SGK Hình học 10 nâng cao
Cho hình bình hành ABCD. Chứng minh rằng \(\overrightarrow {DA} - \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \).
Hướng dẫn giải:
Ta có \(\overrightarrow {DA} - \overrightarrow {DB} = \overrightarrow {BA} \) mà \(\overrightarrow {BA} = \overrightarrow {CD} \) suy ra \(\overrightarrow {DA} - \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow {CD} + \overrightarrow {DC} = \overrightarrow 0 \)
Bài 19 trang 18 SGK Hình học 10 nâng cao
Chứng minh rằng \(\overrightarrow {AB} = \overrightarrow {CD} \) khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Hướng dẫn giải:
Giả sử \(\overrightarrow {AB} = \overrightarrow {CD} \) và M, N lần lượt là trung điểm của AD, BC.
Ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
\overrightarrow {MA} + \overrightarrow {MD} = \overrightarrow 0 ,\overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \\
\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN} ,\overrightarrow {MN} = \overrightarrow {MD} + \overrightarrow {DC} + \overrightarrow {CN}
\end{array} \right.\\
\Rightarrow 2\overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN} + \overrightarrow {MD} + \overrightarrow {DC} + \overrightarrow {CN} \\
= \left( {\overrightarrow {MA} + \overrightarrow {MD} } \right) + \left( {\overrightarrow {BN} + \overrightarrow {CN} } \right) + \overrightarrow {AB} + \overrightarrow {DC} \\
= \overrightarrow {AB} + \overrightarrow {DC} = \overrightarrow {AB} - \overrightarrow {CD} = \overrightarrow 0
\end{array}\)
Do đó, \(\overrightarrow {MN} = \overrightarrow 0 \), tức là M ≡ N.
Vậy trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Ngược lại, ta giả sử trung điểm của hai đoạn thẳng AD và BC trùng nhau, suy ra:
\({\overrightarrow {MA} + \overrightarrow {MD} = \overrightarrow 0 ,\overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 }\)
Suy ra \(\overrightarrow {AB} = \overrightarrow {AM} + \overrightarrow {MB} = \overrightarrow {CM} + \overrightarrow {MD} = \overrightarrow {CD} \)
Bài 20 trang 18 SGK Hình học 10 nâng cao
Cho sáu điểm A, B, C, D, E, F. Chứng minh rằng
\(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CD} = \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} \)
Hướng dẫn giải:
Theo quy tắc ba điểm, ta có:
\(\begin{array}{l}
\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \left( {\overrightarrow {AE} + \overrightarrow {ED} } \right) + \left( {\overrightarrow {BF} + \overrightarrow {FE} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DF} } \right)\\
= \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CD} + \left( {\overrightarrow {FE} + \overrightarrow {ED} + \overrightarrow {DF} } \right)\\
= \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CD} + \left( {\overrightarrow {FD} + \overrightarrow {DF} } \right)\,\\
= \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CD} + \overrightarrow 0 \\
= \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CD}
\end{array}\)
Tương tự, ta có:
\(\begin{array}{l}
\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \left( {\overrightarrow {AF} + \overrightarrow {FD} } \right) + \left( {\overrightarrow {BD} + \overrightarrow {DE} } \right) + \left( {\overrightarrow {CE} + \overrightarrow {EF} } \right)\\
= \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} + \left( {\overrightarrow {FD} + \overrightarrow {DE} + \overrightarrow {EF} } \right)\\
= \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} + \left( {\overrightarrow {FE} + \overrightarrow {EF} } \right)\,\\
= \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} + \overrightarrow 0 \\
= \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE}
\end{array}\)
Vậy \(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CD} = \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} \)
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 1 Bài 3 Hiệu của hai vectơ với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.
