Bài 36 trang 127 SGK Toán 10 nâng cao
Giải và biện luận các bất phương trình:
a) mx + 4 > 2x + m2
b) 2mx + 1 ≥ x + 4m2
c) x(m2 - 1) < m4 - 1
d) 2(m+1)x ≤ (m+1)2(x-1)
Hướng dẫn giải:
Câu a:
mx + 4 > 2x+m2 ⇔ (m - 2)x > m2 - 4 (1)
Nếu m = 2, bất phương trình trở thành 0x > 0 nên vô nghiệm
Nếu m > 2, thì (1) ⇔ x > m + 2 hay tập nghiệm là S = (m + 2;+∞)
Nếu m < 2, thì (1) ⇔ x < m + 2 hay tập nghiệm là S = (-∞;m + 2)
Câu b:
2mx + 1 ≥ 4m2 ⇔ x(2m+1) ≥ (2m - 1)(2m + 1) (2)
Nếu
Nếu
Nếu
Câu c:
x(m2 - 1) < m4 - 1 (3)
Nếu m = 1 hoặc m = - 1, bất phương trình vô nghiệm
Nếu -1 < m < 1 thì (3) ⇔ x > m2 + 1 hay có tập nghiệm là (m2+1;+∞)
Nếu m < - 1 hoặc m > 1 thì (3) ⇔ x < m2+1 hay có tập nghiệm là (-∞;m2+1)
Câu d:
2(m+1)x ≤ (m+1)2(x-1) ⇔ x(m + 1)(m - 1) ≥ (m+1)2 (4)
Nếu m = -1, bất phương trình có nghiệm là R
Nếu m = 1, bất phương trình vô nghiệm
Nếu -1 < m < 1, (4) ⇔ x ≤
Nếu m < - 1 hoặc m > 1, (4) ⇔ x ≥
Bài 37 trang 127 SGK Toán 10 nâng cao
Giải các bất phương trình
a)
b)
c)
d)
Hướng dẫn giải:
Câu a:
Bảng xét dấu
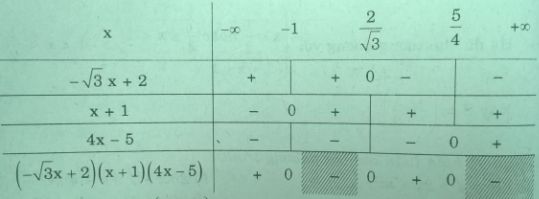
Vậy tập nghiệm của bất phương trình là
Câu b:
Bảng xét dấu

Vậy tập nghiệm là
Câu c:
Ta có
Bảng xét dấu
Vậy tập nghiệm là
Câu d:
Ta có
Bảng xét dấu

Vậy tập nghiệm của bất phương trình là
Bài 38 trang 127 SGK Toán 10 nâng cao
Giải và biện luận các bất phương trình
a)
b)
Hướng dẫn giải:
Câu a:
Ta có:
Với
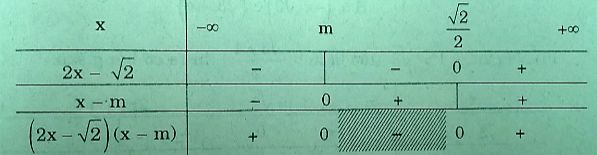
Suy ra
Với
Suy ra
Với
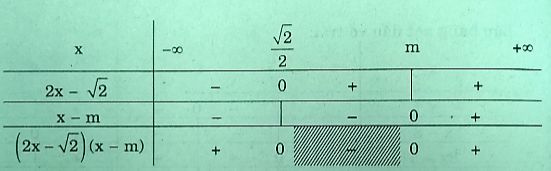
Suy ra
Câu b:
Ta có:
Với

Suy ra
Với
Bảng xét dấu
Với
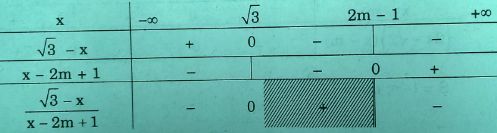
Vậy tập nghiệm là
Bài 39 trang 127 SGK Toán 10 nâng cao
Tìm nghiệm nguyên của mỗi hệ bất phương trình sau:
a)
b)
Hướng dẫn giải:
Câu a:
Vì x ∈ Z nên x ∈ {4, 5, 6, 7, 8, 9, 10, 11}
Vậy tập nghiệm của hệ là : {4, 5, 6, 7, 8, 9, 10, 11}
Câu b:
Vì x ∈ Z nên x = 1
Vậy tập nghiệm của hệ là {1}
Bài 40 trang 127 SGK Toán 10 nâng cao
Giải phương trình và bất phương trình
a)
b)
Hướng dẫn giải:
Câu a:
Bảng xét dấu
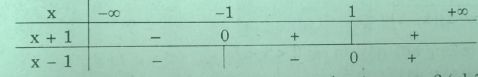
Với x < - 1, ta có
Với
Với x > 1, ta có
Vậy S = {- 2;2}
Câu b:
Nếu thì bất phương trình trở thành:
Bảng xét dấu
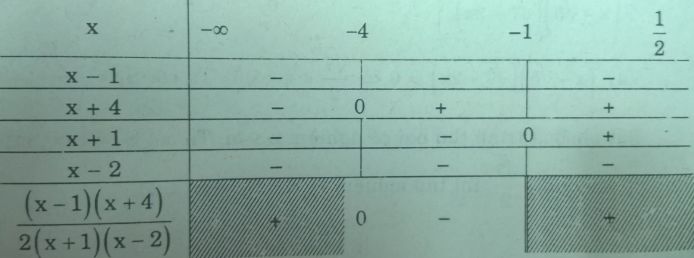
Suy ra tập nghiệm
Nếu
Bảng xét dấu
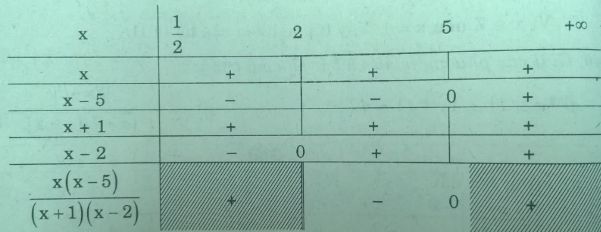
Suy ra tập nghiệm
Vậy tập nghiệm của bất phương trình đã cho là
Bài 41 trang 127 SGK Toán 10 nâng cao
Giải và biện luận bất phương trình
a)
b)
Hướng dẫn giải:
Câu a:
Giải (1):
Bảng xét dấu
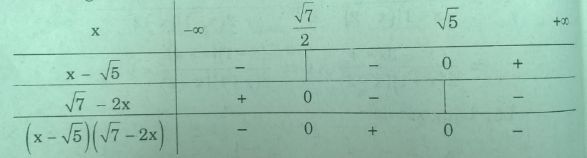
Suy ra
Ta có
Do đó:
Nếu
Nếu
Nếu
Câu b:
Bằng cách lập bảng xét dấu, ta có tập nghiệm của (1) là
Ta lại có
Do đó:
Nếu
Nếu
Nếu
Nếu m > 3 thì tập nghiệm là
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 4 Luyện tập (trang 127) với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.


.PNG)
.PNG)




Thảo luận về Bài viết