Bài 32 trang 126 SGK Toán 10 nâng cao
Lập bảng xét dấu của các biểu thức
a)
b)
c)
d)
Hướng dẫn giải:
Câu a:
Đặt
Ta có:
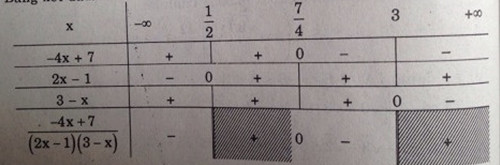
Bảng xét dấu
.jpg?enablejsapi=1)
Vậy
Câu b:
Đặt
Ta có:
Bảng xét dấu
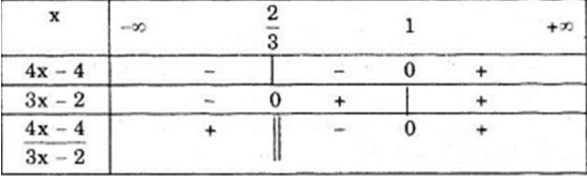
Vậy
Câu c:
Đặt
Ta có:
Bảng xét dấu
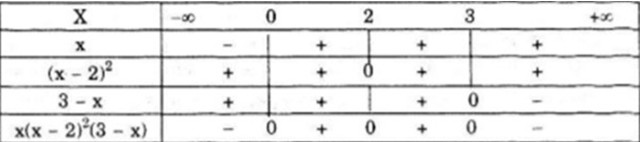
Vậy
Câu d:
Đặt
Ta có:
Bảng xét dấu
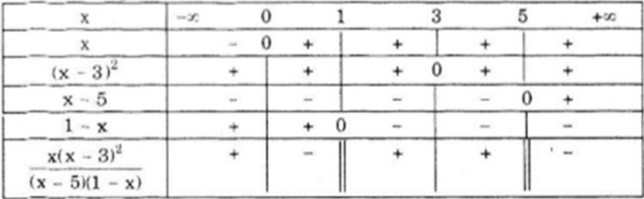
Vậy
Bài 33 trang 126 SGK Toán 10 nâng cao
Phân tích các đa thức sau thành nhân tử bậc nhất rồi xét dấu:
a)
b)
Hướng dẫn giải:
Câu a:
Đặt
Ta có
Bảng xét dấu
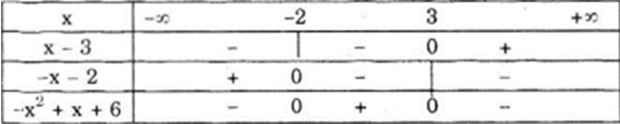
Vậy
Câu b:
Đặt
Ta có
Bảng xét dấu
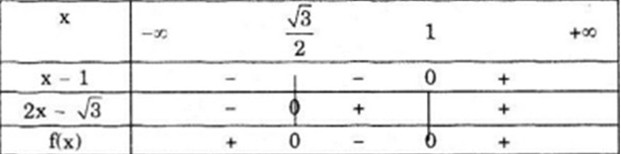
Vậy
Bài 34 trang 126 SGK Toán 10 nâng cao
Giải các bất phương trình
a)
b)
c)
d)
Hướng dẫn giải:
Câu a:
Ta có:
Bảng xét dấu
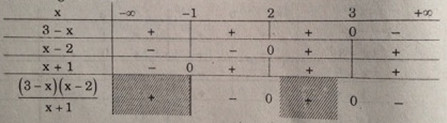
Vậy tập nghiệm là
Câu b:
Ta có
Bảng xét dấu
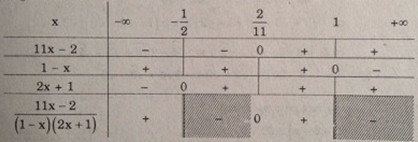
Vậy tập nghiệm của bất phương trình đã cho là
Câu c:
Bảng xét dấu

Với
Kết hợp với điều kiện ta có
Với
Kết hợp với điều kiện ta có
Với
Vậy tập nghiệm của bất phương trình là
Câu d:
Vậy
Bài 35 trang 126 SGK Toán 10 nâng cao
Giải các hệ phương trình
a)
b)
Hướng dẫn giải:
Câu a:
Giải (1):
Bảng xét dấu
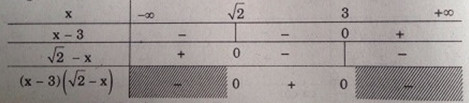
Suy ra tập nghiệm
Giải (2):
Vậy
Câu b:
Giải (1):
Bảng xét dấu
Suy ra tập nghiệm
Kết hợp với - 1 < x < 1 ta có tập nghiệm của hệ là






Thảo luận về Bài viết