Bài 21 trang 23 SGK Hình học 10 nâng cao
Cho tam giác vuông cân OAB với OA = OB = a. Hãy dựng các vec tơ sau đây và tính độ dài của chúng
\(\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} ;\\
\overrightarrow {OA} - \overrightarrow {OB} ;\\
3\overrightarrow {OA} + 4\overrightarrow {OB} ;\\
\frac{{21}}{4}\overrightarrow {OA} + 2,5\overrightarrow {OB} ;\\
\frac{{11}}{4}\overrightarrow {OA} - \frac{3}{7}\overrightarrow {OB} .
\end{array}\)
Hướng dẫn giải:
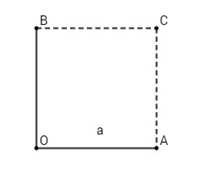
Vẽ hình vuông OACB, ta có:
\(\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {OC} } \right| = a\sqrt 2 \\
\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \Rightarrow \left| {\overrightarrow {OA} - \overrightarrow {OB} } \right| = \left| {\overrightarrow {BA} } \right| = a\sqrt 2
\end{array}\)
Gọi M, N là điểm thỏa mãn \(\overrightarrow {OM} = 3\overrightarrow {OA} ,\overrightarrow {ON} = 4\overrightarrow {OB} \)
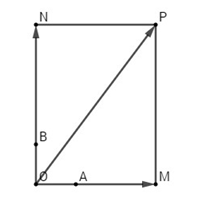
Vẽ hình chữ nhật MONP, ta có:
\(\begin{array}{l}
\overrightarrow {OM} + \overrightarrow {ON} = \,\overrightarrow {OP} \Rightarrow \left| {\overrightarrow {OM} + \overrightarrow {ON} } \right| = \left| {\overrightarrow {OP} } \right| = \sqrt {O{M^2} + O{N^2}} \\
= \sqrt {9{a^2} + 16{a^2}} = 5a
\end{array}\)
Tương tự, ta có: \(\left| {\frac{{21}}{4}\overrightarrow {OA} + 2,5\overrightarrow {OB} } \right| = \sqrt {{{\left( {\frac{{21}}{4}a} \right)}^2} + {{\left( {\frac{5}{2}a} \right)}^2}} = \frac{{\sqrt {241} }}{4}a\)
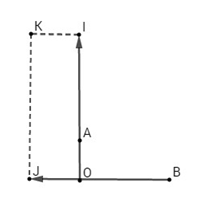
Gọi I, J là điểm thỏa mãn:
\(\overrightarrow {OI} = \frac{{11}}{4}\overrightarrow {OA} ;\overrightarrow {OJ} = - \frac{3}{7}\overrightarrow {OB} \)
Vẽ hình chữ nhật OIKJ, ta có:
\(\begin{array}{l}
\frac{{11}}{4}\overrightarrow {OA} - \frac{3}{7}\overrightarrow {OB} = \frac{{11}}{4}\overrightarrow {OA} + \left( { - \frac{3}{7}} \right)\overrightarrow {OB} = \overrightarrow {OI} + \overrightarrow {OJ} = \overrightarrow {OK} \\
\Rightarrow \left| {\frac{{11}}{4}\overrightarrow {OA} - \frac{3}{7}\overrightarrow {OB} } \right| = \left| {\overrightarrow {OK} } \right| = \sqrt {{{\left( {\frac{{11}}{4}a} \right)}^2} + {{\left( { - \frac{3}{7}a} \right)}^2}} = \frac{{\sqrt {6073} }}{{28}}a
\end{array}\)
Bài 22 trang 23 SGK Hình học 10 nâng cao
Cho tam giác OAB. Gọi M, N lần lượt là trung điểm hai cạnh OA và OB. Hãy tìm các số mm và nn thích hợp trong mỗi đẳng thức sau đây:
\(\begin{array}{l}
\overrightarrow {OM} = m\overrightarrow {OA} + n\overrightarrow {OB} ;\,\,\,\overrightarrow {MN} = m\overrightarrow {OA} + n\overrightarrow {OB} ;\\
\overrightarrow {AN} = m\overrightarrow {OA} + n\overrightarrow {OB} ;\,\,\,\,\overrightarrow {MB} = m\overrightarrow {OA} + n\overrightarrow {OB.}
\end{array}\)
Hướng dẫn giải:
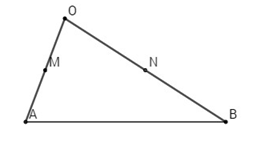
Ta có:
\(\begin{array}{l}
\overrightarrow {OM} = \frac{1}{2}\overrightarrow {OA} = \frac{1}{2}\overrightarrow {OA} + 0.\overrightarrow {OB} \Rightarrow m = \frac{1}{2},n = 0\\
\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} = \frac{1}{2}\overrightarrow {OB} - \frac{1}{2}\overrightarrow {OA} \\
= \left( { - \frac{1}{2}} \right)\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} \Rightarrow m = - \frac{1}{2},n = \frac{1}{2}\\
\overrightarrow {AN} = \overrightarrow {ON} - \overrightarrow {OA} = \frac{1}{2}\overrightarrow {OB} - \overrightarrow {OA} \\
= \left( { - 1} \right)\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} \Rightarrow m = - 1,n = \frac{1}{2}\,\\
\overrightarrow {MB} = \overrightarrow {OB} - \overrightarrow {OM} = \overrightarrow {OB} - \frac{1}{2}\overrightarrow {OA} \\
= \left( { - \frac{1}{2}} \right)\overrightarrow {OA} + \overrightarrow {OB} \Rightarrow m = - \frac{1}{2},n = 1
\end{array}\)
Bài 23 trang 24 SGK Hình học 10 nâng cao
Gọi M và N lần lượt là trung điểm các đoạn thẳng AB và CD. Chứng minh rằng:
\(2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overrightarrow {BC} \)
Hướng dẫn giải:
Theo quy tắc ba điểm, ta có:
\(\begin{array}{l}
\overrightarrow {AC} + \overrightarrow {BD} = \left( {\overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} } \right) + \left( {\overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} } \right)\\
= 2\overrightarrow {MN} + \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right)\\
= 2\overrightarrow {MN} + \overrightarrow 0 + \overrightarrow 0 = 2\overrightarrow {MN} \\
\overrightarrow {AD} + \overrightarrow {BC} = \left( {\overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} } \right) + \left( {\overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} } \right)\\
= 2\overrightarrow {MN} + \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right)\\
= 2\overrightarrow {MN} + \overrightarrow 0 + \overrightarrow 0 = 2\overrightarrow {MN}
\end{array}\)
Vậy \(2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overrightarrow {BC} \)
Bài 24 trang 24 SGK Hình học 10 nâng cao
Cho tam giác ABC và điểm G. Chứng minh rằng
a) Nếu \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) thì G là trọng tâm tam giác ABC;
b) Nếu có điểm O sao cho \(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\) thì G là trọng tâm tam giác ABC.
Hướng dẫn giải:
Câu a:
Gọi G1 là trọng tâm tam giác ABC. Từ đó, ta có \({\overrightarrow {{G_1}A} + \overrightarrow {{G_1}B} + \overrightarrow {{G_1}C} = \overrightarrow 0 }\).
Theo giả thiết, \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
\(\begin{array}{l}
\Rightarrow \overrightarrow {G{G_1}} + \overrightarrow {{G_1}A} + \overrightarrow {{G_1}B} + \overrightarrow {{G_1}C} = \overrightarrow 0 \\
\Rightarrow 3\overrightarrow {G{G_1}} + \left( {\overrightarrow {{G_1}A} + \overrightarrow {{G_1}B} + \overrightarrow {{G_1}C} } \right) = \overrightarrow 0 \\
\Rightarrow 3\overrightarrow {G{G_1}} = \overrightarrow 0 \\
\Rightarrow \overrightarrow {G{G_1}} = \overrightarrow 0
\end{array}\)
\( \Rightarrow G \equiv {G_1}\)
Câu b:
Gọi G1 là trọng tâm tam giác ABC. Từ đó, ta có \({\overrightarrow {{G_1}A} + \overrightarrow {{G_1}B} + \overrightarrow {{G_1}C} = \overrightarrow 0 }\).
\(\begin{array}{l}
\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\\
= \frac{1}{3}\left( {3\overrightarrow {O{G_1}} + \overrightarrow {{G_1}A} + \overrightarrow {{G_1}B} + \overrightarrow {{G_1}C} } \right) = \overrightarrow {O{G_1}} \\
\Rightarrow G \equiv {G_1}
\end{array}\)
Bài 25 trang 24 SGK Hình học 10 nâng cao
Gọi G là trọng tâm tam giác ABC. Đặt \(\overrightarrow a = \overrightarrow {GA} \) và \(\overrightarrow b = \overrightarrow {GB} \). Hãy biểu thị mỗi vec tơ \(\overrightarrow {AB} ,\overrightarrow {GC} ,\overrightarrow {BC} ,\overrightarrow {CA} \) qua các vec tơ \(\overrightarrow a\) và \(\overrightarrow b\)
Hướng dẫn giải:
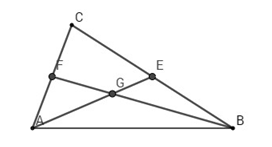
Vì G là trọng tâm tam giác ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
Ta có
\(\begin{array}{l}
\overrightarrow {AB} = \overrightarrow {GB} - \overrightarrow {GA} = \overrightarrow b - \overrightarrow a \\
\overrightarrow {GC} = - \overrightarrow {GB} - \overrightarrow {GA} = - \overrightarrow b - \overrightarrow a \\
\overrightarrow {BC} = \overrightarrow {GC} - \overrightarrow {GB} = - \overrightarrow b - \overrightarrow a - \overrightarrow b = - 2\overrightarrow b - \overrightarrow a \\
\overrightarrow {CA} = \overrightarrow {GA} - \overrightarrow {GC} = \overrightarrow a - \left( { - \overrightarrow b - \overrightarrow a } \right) = 2\overrightarrow a + \overrightarrow b
\end{array}\)
Bài 26 trang 24 SGK Hình học 10 nâng cao
Chứng minh rằng nếu G và G′ lần lượt là trọng tâm tam giác ABC và tam giác A′B′C′ thì
\(3\overrightarrow {GG'} = \overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} \)
Từ đó hãy suy ra điều kiện cần và đủ để hai tam giác ABC và A′B′C′ có trọng tâm trùng nhau.
Hướng dẫn giải:
Vì G là trọng tâm tam giác ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
Vì G′ là trọng tâm tam giác A′B′C′ nên \(\overrightarrow {G'A'} + \overrightarrow {G'B'} + \overrightarrow {G'C'} = \overrightarrow 0 \)
Áp dụng quy tắc ba điểm, ta có:
\(\begin{array}{l}
\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} \\
= \left( {\overrightarrow {AG} + \overrightarrow {GG'} + \overrightarrow {G'A'} } \right) + \left( {\overrightarrow {BG} + \overrightarrow {GG'} + \overrightarrow {G'B'} } \right) + \left( {\overrightarrow {CG} + \overrightarrow {GG'} + \overrightarrow {G'C'} } \right)\\
= 3\overrightarrow {GG'} + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) + \left( {\overrightarrow {G'A'} + \overrightarrow {G'B'} + \overrightarrow {G'C'} } \right) = 3\overrightarrow {GG'}
\end{array}\)
Vậy điều kiện cần và đủ để hai tam giác ABCvà A′B′C′′ có trọng tâm trùng nhau là
\(\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} = \overrightarrow 0 \)
Bài 27 trang 24 SGK Hình học 10 nâng cao
Cho lục giác ABCDEF. Gọi P, Q, R, S, T, U lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác PRT và QSU có trọng tâm trùng nhau.
Hướng dẫn giải:
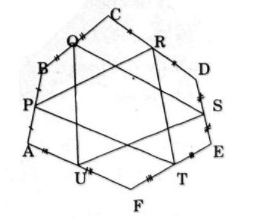
Lấy O bất kì và gọi K, G lần lượt là trọng tâm tam giác PRT và QSU, ta có:
\(\begin{array}{l}
3\overrightarrow {OG} = \overrightarrow {OP} + \overrightarrow {OR} + \overrightarrow {OT} \\
= \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + \frac{1}{2}\left( {\overrightarrow {OC} + \overrightarrow {OD} } \right) + \frac{1}{2}\left( {\overrightarrow {OE} + \overrightarrow {OF} } \right)\\
= \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} + \overrightarrow {OF} } \right)\\
3\overrightarrow {OK} = \overrightarrow {OQ} + \overrightarrow {OS} + \overrightarrow {OU} \\
= \frac{1}{2}\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right) + \frac{1}{2}\left( {\overrightarrow {OD} + \overrightarrow {OE} } \right) + \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OF} } \right)\\
= \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} + \overrightarrow {OF} } \right)
\end{array}\)
Từ (1) và (2) suy ra \(\overrightarrow {OG} = \overrightarrow {OK} \) hay G ≡ K
Vậy hai tam giác PRT và QSU có trọng tâm trùng nhau.
Bài 28 trang 24 SGK Hình học 10 nâng cao
Cho tứ giác ABCD. Chứng minh rằng:
a) Có một điểm G duy nhất sao cho \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0\). Điểm G như thế gọi là trọng tâm của bốn điểm A, B, C, D. Tuy nhiên, người ta vẫn quen gọi G là trọng tâm của từ giác ABCD.
b) Trọng tâm G là trung điểm của mỗi đoạn thẳng nối các trung điểm hai cạnh đối của tứ giác, nó cũng là trung điểm của đoạn thẳng nối trung điểm hai đường chéo của tam giác.
c) Trọng tâm G nằm trên các đoạn thẳng nối một đỉnh của tứ giác và trọng tâm của tam giác tạo bởi ba đỉnh còn lại.
Hướng dẫn giải:
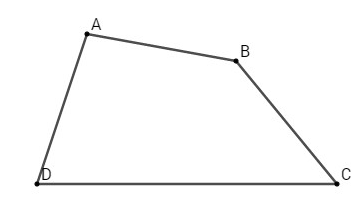
Câu a:
Gọi O là điểm cố định bất kì, ta có:
\(\begin{array}{l}
\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \\
\Leftrightarrow \overrightarrow {OA} - \overrightarrow {OG} + \overrightarrow {OB} - \overrightarrow {OG} + \overrightarrow {OC} - \overrightarrow {OG} + \overrightarrow {OD} - \overrightarrow {OG} = \overrightarrow 0 \\
\Leftrightarrow 4\,\overrightarrow {OG} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \\
\Leftrightarrow \overrightarrow {OG} \, = \frac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)
\end{array}\)
Vậy G là điểm xác định duy nhất sao cho \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
Câu b:
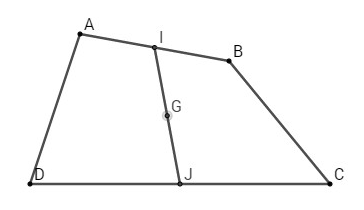
Gọi I, J lần lượt la trung điểm của AB,CD ta có
\(\begin{array}{l}
\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \\
\Rightarrow 2\overrightarrow {GI} + 2\overrightarrow {GJ} = \overrightarrow 0 \\
\Rightarrow \overrightarrow {GI} + \overrightarrow {GJ} = \overrightarrow 0
\end{array}\)
⇒G là trung điểm IJ
Tương tự, ta gọi H, K lần lượt là trung điểm của AC, BD ta có
\(\begin{array}{l}
\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \\
\Rightarrow 2\overrightarrow {GH} + 2\overrightarrow {GK} = \overrightarrow 0 \\
\Rightarrow \overrightarrow {GH} + \overrightarrow {GK} = \overrightarrow 0
\end{array}\)
⇒G là trung điểm HK
Tương tự, ta cũng chứng minh được G là trung điểm của đoạn thẳng nối trung điểm hai đường chéo của tam giác.
Câu c:
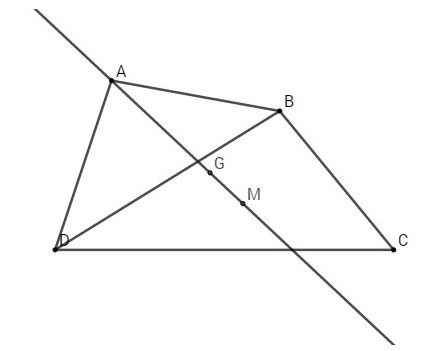
Gọi M là trọng tâm của tam giác BCD, ta có
\(\begin{array}{l}
3\overrightarrow {GM} = \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} \\
\Rightarrow 3\overrightarrow {GM} + \overrightarrow {GA} = \overrightarrow 0 \\
\Rightarrow \overrightarrow {GA} = - 3\overrightarrow {GM}
\end{array}\)
Do đó G, A, M thẳng hàng.
Các trường hợp còn lại làm tương tự.Vậy trọng tâm G nằm trên các đoạn thẳng nối một đỉnh của tứ giác và trọng tâm của tam giác tạo bởi ba đỉnh còn lại.
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 1 Bài 4 Tích của một vectơ với một số với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.
