Bài 39 trang 63 SGK Toán 10 nâng cao
Với mỗi câu sau đây. Hãy chọn phần kết luận mà em cho là đúng:
a) Trên khoảng (-1; 1), hàm số y = - 2x + 5
(A) Đồng biến
(B) Nghịch biến;
(C) Cả kết luận (A) và (B) đều sai.
b) Trên khoảng (0; 1), hàm số y = x2 + 2x - 3
(A) Đồng biến
(B) Nghịch biến;
(C) Cả kết luận (A) và (B) đều sai.
c) Trên khoảng (- 2; 1) hàm số y = x2 + 2x - 3
(A) Đồng biến
(B) Nghịch biến;
(C) Cả kết luận (A) và (B) đều sai.
Hướng dẫn giải:
a) Kết luận (B);
b) Kết luận (A);
c) Kết luận (C).
Bài 40 trang 63 SGK Toán 10 nâng cao
a) Tìm các hàm số lẻ trong các hàm số bậc nhất \(y=ax+b\)
b) Tìm các hàm số chẫn trong các hàm số bậc hai \(y=ax^2+bx+c\)
Hướng dẫn giải:
Câu a:
Đặt \(f\left( x \right) = ax + b\,\,\left( {a \ne 0} \right)\)
\(y=f(x)\) là hàm số lẻ khi \(f\left( { - x} \right) = - f\left( x \right),\forall x \in R\)
\( \Leftrightarrow - ax + b = - \left( {ax + b} \right) \Leftrightarrow b = 0\)
Vậy với \(a \ne 0,b = 0\) thì \(y=ax+b\) là hàm số lẻ.
Câu b:
Đặt \(f\left( x \right) = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\)
\(y=f(x)\) là hàm số chẫn khi \(f\left( { - x} \right) = f\left( x \right),\forall x \in R\)
\(\begin{array}{l}
\Leftrightarrow a{x^2} - bx + c = a{x^2} + bx + c,\forall x \in R\\
\Leftrightarrow 2bx = 0,\forall x \in R \Leftrightarrow b = 0
\end{array}\)
Vậy với \(a \ne 0,b = 0,c\) tùy ý thì hàm số \(y=ax^2+bx+c\) là hàm số chẫn.
Bài 41 trang 63 SGK Toán 10 nâng cao
Dựa vào đồ thị của hàm số \(y=ax^2+bx+c\). Hãy xác định dấu của các hệ số a, b và c trong mỗi trường hợp dưới đây:
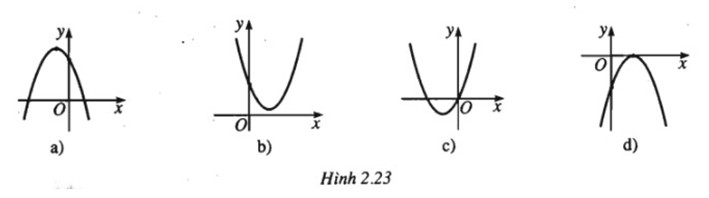
Hướng dẫn giải:
Câu a:
Parabol (P1) có bề lõm quay xuống nên \(a < 0\)
(P1) cắt trục Oy tại điểm có tung độ dương nên \(c = f(0) > 0\)
Hoành độ đỉnh \({x_0} = - \frac{b}{{2a}} < 0 \Rightarrow b < 0\) (do \(a < 0\))
Câu b:
Parabol (P2) có bề lõm quay lên nên \(a > 0\)
(P2) cắt trục Oy tại điểm có tung độ dương nên \(c = f(0) > 0\)
Hoành độ đỉnh \({x_0} = - \frac{b}{{2a}} > 0 \Rightarrow b < 0\) (do \(a >0\))
Câu c:
Parabol (P3) có bề lõm quay lên nên \(a > 0\)
(P3) đi qua gốc O nên \(c = 0\)
Hoành độ đỉnh \({x_0} = - \frac{b}{{2a}} < 0 \Rightarrow b > 0\) (do \(a >0\))
Câu d:
Parabol (P4) có bề lõm quay xuống nên \(a < 0\)
(P4) cắt trục Oy tại điểm có tung độ âm nên \(c < 0\)
Hoành độ đỉnh \({x_0} = - \frac{b}{{2a}} > 0 \Rightarrow b > 0\) (do \(a < 0\))
Bài 42 trang 63 SGK Toán 10 nâng cao
Trong mỗi trường hợp cho dưới đây, hãy vẽ đồ thị hàm số của các hàm số trên cùng một hệ trục tọa độ rồi xác định tọa độ giao điểm của chúng.
a) \(y=x-1\) và \(y=x^2-2x-1\)
b) \(y=-x+3\) và \(y=-x^2-4x+1\)
c) \(y=2x-5\) và \(y=x^2-4x-1\)
Hướng dẫn giải:
Câu a:
Đường thẳng \(d: y=x-1\) qua A(0;- 1); B(1;0)
Parabol (P): \(y=x^2-2x-1\) có đỉnh S(1;- 2)
Phương trình hoành độ giao điểm của d và (P) là:
\({x^2} - 2x - 1 = x - 1 \Leftrightarrow {x^2} - 3x = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\left( {y = - 1} \right)\\
x = 3\left( {y = 2} \right)
\end{array} \right.\)
Giao điểm của d và (P) là A(0;- 1) và C(3;2)
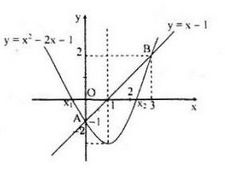
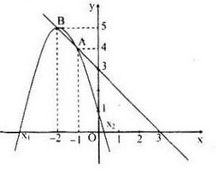
Câu b:
Đường thẳng \(d: y=-x+3\) qua A(0;3); B(3;0)
Parabol (P): \(y=-x^2-4x+1\) có đỉnh S(- 2;5)
Phương trình hoành độ giao điểm của d và (P) là:
\(\begin{array}{l}
- {x^2} - 4x + 1 = - x + 3\\
\Leftrightarrow {x^2} + 3x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}
x = - 1\left( {y = 4} \right)\\
x = - 2\left( {y = 5} \right)
\end{array} \right.
\end{array}\)
Giao điểm của d và (P) là (- 1;4) và (- 2;5)
Câu c:
Đường thẳng \(d: y=2x-5\) đi qua A(0;- 5); B(1;- 3)
Parabol (P): \(y=x^2-4x-1\) có điểnh S(2;- 5)
Phương trình hoành độ giao điểm của d và (P) là:
\(\begin{array}{l}
{x^2} - 4x - 1 = 2x - 5\\
\Leftrightarrow {x^2} - 6x + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 3 - \sqrt 5 \left( {y = 1 - 2\sqrt 5 } \right)\\
x = 3 + \sqrt 5 \left( {y = 1 + 2\sqrt 5 } \right)
\end{array} \right.
\end{array}\)
Giao điểm của d và (P) là \(\left( {3 - \sqrt 5 ;1 - 2\sqrt 5 } \right);\left( {3 + \sqrt 5 ;1 + 2\sqrt 5 } \right)\)
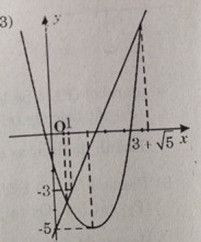
Bài 43 trang 63 SGK Toán 10 nâng cao
Xác định các hệ số a, b và c để cho hàm số \(y=ax^2+bx+c\) đạt giá trị nhỏ nhất bằng \(\frac{3}{4}\) khi \(x = \frac{1}{2}\) và nhận giá trị bằng 1 khi x = 1. Lập bảng biến thiên và vẽ đồ thị của hàm số.
Hướng dẫn giải:
Đặt \(f(x)=ax^2+bx+c\)
Ta có \(\left\{ \begin{array}{l}
{x_1} = - \frac{b}{{2a}}\\
f\left( {\frac{1}{2}} \right) = \frac{1}{4}a + \frac{1}{2}b + c\\
f\left( 1 \right) = a + b + c
\end{array} \right.\)
Tìm hệ số \(a, b, c\) thỏa hệ:
\(\left\{ \begin{array}{l}
- \frac{b}{{2a}} = \frac{1}{2}\\
\frac{1}{4}a + \frac{1}{2}b + c = \frac{3}{4}\\
a + b + c = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a + b = 0\\
a + 2b + 4 = 3\\
a + b + c = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a = 1\\
b = - 1\\
c = 1
\end{array} \right.\)
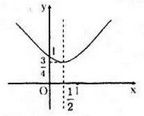
Vậy \(y=x^2-x+1\)
Bảng biến thiên
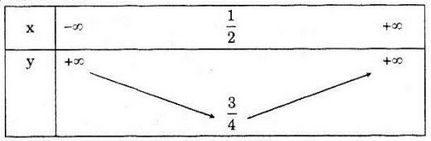
Đồ thị hàm số
Bài 44 trang 64 SGK Toán 10 nâng cao
Vẽ đồ thị của các hàm số sau rồi lập bảng biến thiên của nó
a) \(y = \left| {\frac{3}{2}x - 2} \right|\)
b) \(y = \left\{ \begin{array}{l}
2x,\,\,\,\,\,\,\,\,\,\,\,x < 0\\
{x^2} - x,\,\,\,\,x \ge 0
\end{array} \right.\)
c) \(y = \left| {\frac{1}{2}{x^2} + x - \frac{3}{2}} \right|\)
d) \(y = x\left| x \right| - 2x - 1\)
Hướng dẫn giải:
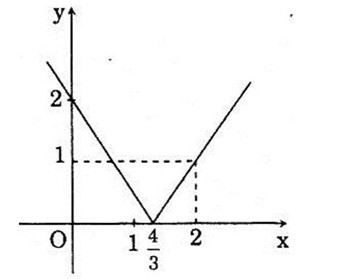
Câu a:
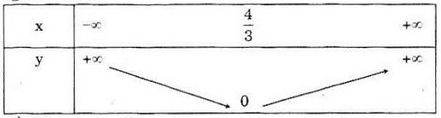
Ta có \(y = \left\{ \begin{array}{l}
\frac{3}{2}x - 2,\,\,\,\,\,\,\,x \ge \frac{3}{4}\\
- \frac{3}{2}x + 2,\,\,\,\,x < \frac{3}{4}
\end{array} \right.\)
Đồ thị hàm số
Bảng biến thiên
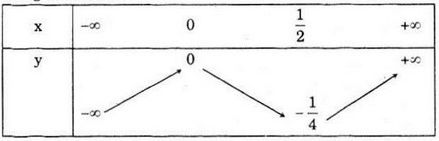
Câu b:
Đồ thị hàm số
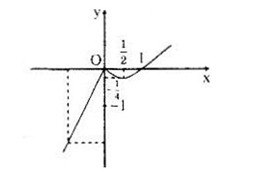
Bảng biến thiên
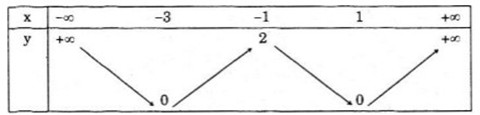
Câu c:
Ta có \(y = \left\{ \begin{array}{l}
\frac{1}{2}{x^2} + x - \frac{3}{2},\,\,\,\,\,\,x \le - 3,x \ge - 1\\
- \frac{1}{2}{x^2} - x + \frac{3}{2},\,\, - 3 < x < 1
\end{array} \right.\)
Đồ thị hàm số
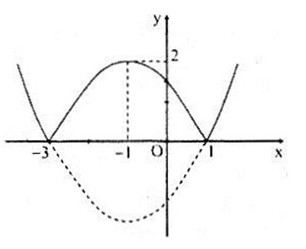
Bảng biến thiên
Câu d:
Ta có \(y = \left\{ {\begin{array}{*{20}{l}}
{{x^2} - 2x - 1,{\mkern 1mu} {\mkern 1mu} x \ge 0}\\
{ - {{\left( {x + 1} \right)}^2},{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x < 0}
\end{array}} \right.\)
Đồ thị hàm số
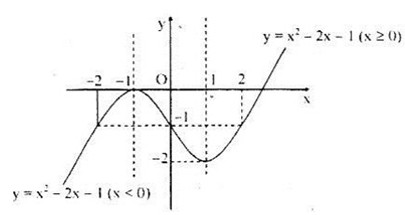
Bảng biến thiên

Bài 45 trang 64 SGK Toán 10 nâng cao
Khi một con tàu vũ trụ được phóng lên Mặt Trăng, trước hết nó sẽ bay vòng quanh Trái Đất. Sau đó, đến một thời điểm thích hợp, động cơ bắt đầu hoạt động đưa con tàu bay theo quỹ đạo là một nhánh hình parabol lên Mặt Trăng (trong hệ tọa độ Oxy như hình vẽ bên, X và y tính bằng nghìn kilômét). Biết rằng khi động cơ bắt đầu hoạt động, x = 0 thì y = - 7. Sau đó y = - 4 khi x = 10 và y = 5 khi x = 20.
a) Tìm hàm số có đồ thị là nhánh parabol nói trên.
b) Theo lịch trình, đế đến được Mặt Trăng, con tàu phải đi qua điểm (100;V) với \(y = 294 \pm 1,5\). Hỏi điều kiện đó có được thỏa màn hay không?
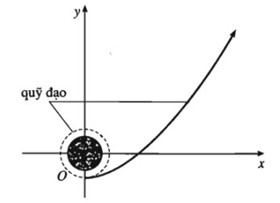
Hướng dẫn giải:
Câu a:
Gọi hàm số bậc hai cần tìm là \(y=f(x)=ax^2+bx+c\)
Theo đề bài ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
f\left( 0 \right) = - 7\\
f\left( {10} \right) = - 4\\
f\left( {20} \right) = 5
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
c = - 7\\
100a + 10b + c = - 4\\
400a + 20b + c = 5
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
a = 0,03\\
b = 0\\
c = - 7
\end{array} \right.
\end{array}\)
Vậy \(y = 0,03{x^2} - 7\)
Câu b:
Theo điều kiện khi x = 100 thì \(y = 294 \pm 1,5\)
Tức \(294 - 1,5 \le y \le 294 + 1,5\)
\( \Leftrightarrow y \in \left[ {292,5;295,5} \right]\)
Ta có \(f\left( {100} \right) = 0,{03.100^2} - 7 = 293\) (thỏa mãn điều kiện)
Bài 46 trang 64 SGK Toán 10 nâng cao
Trên hình bên, điểm M chuyển động trên đoạn thẳng AX. Từ M, kẻ đường thẳng song song với AB, cắt một trong ba đoạn thẳng BC, DE, FG tại điểm N. Gọi S là diện tích của miền tô đậm nằm ở bên trái MN. Gọi độ dài đoạn AM là x (0 < x < 9). Khi đó S là một hàm số của biến x. Hãy nêu biểu thức xác định hàm số S(x).
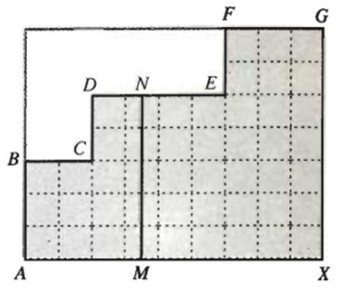
Hướng dẫn giải:
Với x ≤ x < 2 thì S(x) = AM.AB = 3x
Với 2 ≤ x < 6 thì S(x) = AB.BC + MN.DN = 6 + 5(x – 2) = 5x – 4
Với 6 ≤ x ≤ 9 thì S(x) = 6 + 20 +7(x – 6) = 7x – 16
Vậy \(S\left( x \right) = \left\{ \begin{array}{l}
3x,\,\,\,\,\,\,\,\,\,\,\,\,0 \le x < 2\\
5x - 4,\,\,\,\,\,2 \le x < 6\\
7x - 16,\,\,6 \le x \le 9
\end{array} \right.\)
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Ôn tập chương 2 với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.





