Bài 20 trang 53 SGK Toán 10 nâng cao
Có phải mọi đường thẳng trong mặt phẳng toạ độ đều là đồ thị của một hàm số nào đó không ? Vì sao?
Hướng dẫn giải:
Không phải. Vì mỗi đường thẳng trong mặt phẳng tọa độ đều là đồ thị của một hàm số nào đó, với các đường thẳng cùng phương với trục tung (có phương trình x = a) không là đồ thị của một hàm số.
Bài 21 trang 53 SGK Toán 10 nâng cao
a) Tìm hàm số
b) Vẽ đồ thị của hàm số tìm được.
Hướng dẫn giải:
Câu a:
Đồ thị hàm số
Do đó:
Đường thẳng đi qua điểm (- 2;5) nên:
Vậy
Câu b:
Đồ thị hàm số
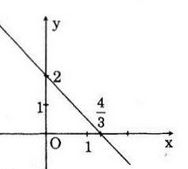
Bài 22 trang 53 SGK Toán 10 nâng cao
Tìm bốn hàm số bậc nhất của đồ thị là bốn đường thẳng đôi một cắt nhau tại bốn đỉnh của một hình vuông nhận gốc O làm tâm đối xứng, biết rằng một đỉnh của hình vuông này là A(3;0).
Hướng dẫn giải:
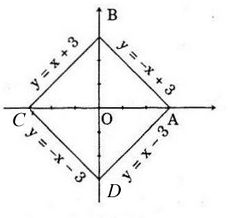
Vì O là tâm đối xứng của hình vuông và có đỉnh A(3;0) nên các đỉnh còn lại của hình vuông là: B(0;3);C(−3;0);D(0;−3)
Đường thẳng đi qua hai điểm A, B có dạng y = ax+b
A(3;0); B(0;3) nằm trên đường thẳng nên:
Vậy AB: y = - x + 3
Tương tự:
BC: y = x + 3
CD: y = - x - 3
DA: y = x - 3
Bài 23 trang 53 SGK Toán 10 nâng cao
Gọi (G) là đồ thị của hàm số y = 2|x|
a) Khi tịnh tiến (G) lên trên 3 đơn vị, ta được đồ thị của hàm số nào ?
b) Khi tịnh tiến (G) sang trái 1 đơn vị, ta được đồ thị của hàm số nào ?
c) Khi tịnh tiến (G) sang phải 2 đơn vị, rồi xuống dưới 1 đơn vị, ta được đồ thị của hàm số nào?
Hướng dẫn giải:
Câu a:
Khi tịnh tiến (G) lên trên 3 đơn vị, ta được đồ thị của hàm số y = 2|x| + 3
Câu b:
Khi tịnh tiến (G) sang trái 1 đơn vị, ta được đồ thị của hàm số y = 2|x + 1|
Câu c:
Khi tịnh tiến (G) sang phải 2 đơn vị, rồi xuống dưới 1 đơn vị, ta được đồ thị của hàm số y = 2|x – 2| - 1
Bài 24 trang 53 SGK Toán 10 nâng cao
Vẽ đồ thị của hai hàm số sau trên cùng một mặt phẳng tọa độ và nêu nhận xét về quan hệ giữa chúng:
a) y = |x – 2|
b) y = |x| - 3
Hướng dẫn giải:
Ta có:
Bảng giá trị
| x | 0 | 2 |
| y = x - 2 | - 2 | 0 |
| y = - x + 2 | 2 | 0 |
| x | 0 | 1 |
| y = x - 3 | - 3 | - 2 |
| y = - x - 3 | - 3 | - 4 |
Đồ thị hàm số
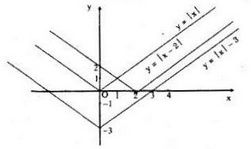
Đồ thị của hàm số y = |x| - 3 có được do tịnh tiến liên tiếp đồ thị hàm số y = |x - 2| sang trái 2 đơn vị và xuống dưới 3 đơn vị.
Ta có: y = |x| - 3 = |(x - 2) + 2| - 3
Bài 25 trang 54 SGK Toán 10 nâng cao
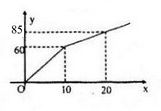
Đi một hãng taxi quy định giá thuê xe đi mỗi kilômét là 6 nghìn đồng đối 10 km đầu tiên và 2,5 nghìn đồng đối với các kilômét tiếp theo. Một khách thuê taxi đi quãng đường x kilômét phải trả số tiền là y nghìn đồng. Khi đó, y là một hàm số của đối số x, xác định với mọi x ≥ 0.
a) Hãy biểu diễn y như một hàm số bậc nhất trên từng khoảng ứng với đoạn [0;10] và khoảng (10;+∞)
b) Tính
c) Vẽ đồ thị của hàm số
Hướng dẫn giải:
Câu a:
Ta có
Nếu
Nếu
Vậy
Câu b:
Ta có:
Câu c:
Bảng giá trị
| x | 0 | 10 |
| y = 6x | 0 | 60 |
| y = 2,5x + 35 | 35 | 60 |
Bảng biến thiên

Đồ thị hàm số
Bài 26 trang 54 SGK Toán 10 nâng cao
Cho hàm số: y = 3|x – 1| - |2x + 2|
a) Bằng cách bỏ dấu giá trị tuyệt đối, hãy viết hàm số đã cho dưới dạng hàm số bậc nhất trên từng khoảng.
(Hướng dẫn: Xét các khoảng hay đoạn
b) Vẽ đồ thị rồi lập bảng biến thiên của hàm số đã cho.
Hướng dẫn giải:
Câu a:
Ta có:
- Với
- Với
- Với
Vậy
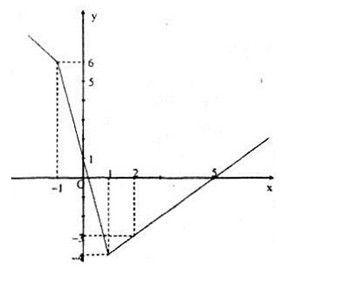
b) Bảng giá trị
| x | - 1 | 1 |
| y = - x + 5 | 6 | 4 |
| y = - 5x + 1 | 6 | - 4 |
| y = x - 5 | - 6 | - 4 |
Bảng biến thiên
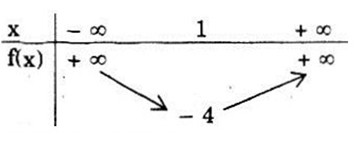
Đồ thị hàm số
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 2 Luyện tập (trang 53, 54) với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.






Thảo luận về Bài viết