Giải Toán 10 SGK nâng cao Chương 2 Bài 3 Hàm số bậc hai

Cho các hàm số 

a) $y=-x^2-3$

b) $y=(x-3{)}^2$

c) $y=\sqrt{2}{x}^2+1$

d) $y=-\sqrt{2}{\left(x+1\right)}^2$

Không vẽ đồ thị, hãy mô tả đồ thị của mỗi hàm số trên bằng cách điền vào chỗ trống (...) theo mẫu:

- Đỉnh của parabol là điểm có tọa độ...

- Parabol có trục đối xứng là đường thẳng...

- Parabol hướng bề lõm (lên trên/ xuống dưới)...

Hướng dẫn giải:

Câu a:

Đồ thị hàm số $y=-x^2-3$

– Đỉnh của parabol là điểm có tọa độ (0; -3);

- Parabol có trục đối xứng là đường thẳng x = 0

- Parabol hướng bề lõm xuống dưới.

Câu b:

Đồ thị hàm số $y=(x-3{)}^2$

- Đỉnh của parabol là điểm có tọa độ (3; 0);

- Parabol có trục đối xứng là đường thẳng x = 3;

- Parabol hướng bề lõm lên trên.

Câu c:

Đồ thị hàm số $y=\sqrt{2}{x}^2+1$

- Đỉnh của parabol là điểm có tọa độ (0; 1);

- Parabol có trục đối xứng là đường thẳng x = 0;

- Parabol hướng bề lõm về phía trên.

Câu d:

Đồ thị hàm số $y=-\sqrt{2}{\left(x+1\right)}^2$

- Đỉnh của parabol là điểm có tọa độ (-1; 0);

- Parabol có trục đối xứng là đường thẳng x = -1;

- Parabol hướng bề lõm về xuống dưới.

---

Gọi (P) là đồ thị của hàm số y = ax² + c. Tìm a và c trong mỗi trường hợp sau:

a) y nhận giá trị bằng 3 khi x = 2 và có giá trị nhỏ nhất là - 1;

b) Đỉnh của parabol (P) là I(0; 3) và một trong hai giao điểm của (P) với trục hoành là A(- 2; 0).

Hướng dẫn giải:

Câu a:

Ta có

$y\left(2\right)=3\iff 4a+c=3\left(1\right)$

y có giá trị nhỏ nhất là - 1 khi c = - 1 và a > 0

Thay c = - 1 vào (1) ta được a = 1 (nhận)

Vậy a = 1, c = - 1

Câu b:

$I\left(0;3\right)\in \left(P\right)$ nên c = 3

$A\left(-2;0\right)\in \left(P\right)$ nên $4a+c=0\Rightarrow a=-\frac{3}{4}$

Vậy $a=-\frac{3}{4},c=3$

---

Gọi (P) là đồ thị của hàm số y = a(x - m)². Tìm a và m trong mỗi trường hợp sau.

a) Parabol (P) có đỉnh là I(-3; 0) và cắt trục tung tại điểm M(0; -5);

b) Đường thẳng y = 4 cắt (P) tại hai điểm A(-1; 4) và B(3; 4).

Hướng dẫn giải:

Câu a:

(P) có đỉnh I(m;0) nên m = - 3

$M\left(0;-5\right)\in \left(P\right);y=a{\left(x+3\right)}^2$ nên $-5=9a\Rightarrow a=-\frac{5}{9}$

Vậy $a=-\frac{5}{9},m=-3$

Câu b:

$A\left(-1;4\right)\in \left(P\right)$ và $B\left(3;4\right)\in \left(P\right)$ nên:

$\{\begin{array}{l}a{\left(-1-m\right)}^2=4\\ a{\left(3-m\right)}^2=4\end{array}\iff \{\begin{array}{l}a{\left(m+1\right)}^2=4\left(1\right)\\ a{\left(m-3\right)}^2=4\left(2\right)\end{array}$

Từ (1) và (2) suy ra:

${\left(m+1\right)}^2={\left(m-3\right)}^2\iff m=1$

Thay m = 1 vào (1) ta được a = 1

Vậy a = 1, m = 1

---

Viết mỗi hàm số sau đây thành dạng $y=a(x-p{)}^2+q$ từ đó hãy cho biết đồ thị của nó có thể suy ra từ đồ thị hàm số nào nhờ các phép tịnh tiến đồ thị song song với các trục tọa độ và mô tả cụ thể các phép tịnh tiến.
a) $y=x^2-8x+12$

b) $y=-3x^2-12x+9$

Hướng dẫn giải:

Câu a:

Ta có $y=x^2-8x+16-4={\left(x-4\right)}^2-4$

Đồ thị hàm số $y=(x-4{)}^2-4$ có được nhờ tịnh tiến liên tiếp đồ thị hàm số y = x² về phải 4 đơn vị, rồi xuống dưới 4 đơn vị.

Câu b:

Ta có $y=-3\left(x^2+4x+4\right)+21\iff y=-3{\left(x+2\right)}^2+21$

Đồ thị hàm số $y=-3(x+2{)}^2+21$ có được nhờ tịnh tiến liên tiếp đồ thị hàm số y = −3x² sang trái 2 đơn vị, rồi lên trên 21 đơn vị.

---

Hàm số $y=-2x^2-4x+6$ có đồ thị là Parabol (P).

a) Tìm tọa độ đỉnh, phương trình trục đối xứng của (P).

b) Vẽ Parabol (P).

c) Dựa vào đồ thị, hãy cho biết tập hợp các giá trị của x sao cho y ≥ 0

Hướng dẫn giải:

Câu a:

Ta có: $a=-2,b=-4,c=6$

$x_0=-\frac{b}{2a}=\frac{4}{-4}=-1\Rightarrow y_0=-2{\left(-1\right)}^2-4\left(-1\right)+6=8$

Tọa độ đỉnh (P) là: I(- 1;8)

Phương trình trục đối xứng của (P) là: x = - 1

Câu b:

Giao đồ thị (P) với Ox:

$y=0\iff [\begin{array}{l}x=1\\ x=-3\end{array}$

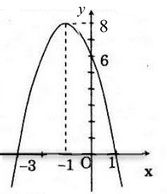
Câu c:

Ta có $y\ge 0\iff -3\le x\le 1$

 

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 2 Bài 3 Hàm số bậc hai với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.