Giải Toán 10 SGK nâng cao Chương 1 Luyện tập (tr 21, 22)

Xác định hai tập hợp A và B biết rằng:

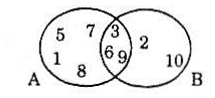
A \ B = {1; 5; 7; 8}, B \ A = {2; 10} và A ∩ B = {3; 6; 9}.

Hướng dẫn giải:

Ta sử dụng biểu đồ Ven

Từ biểu đồ Ven ta có: A = {1; 3; 5; 6; 7; 8; 9}, B = {2; 3; 6; 9; 10}.

---

Cho A = {1; 2; 3; 4; 5; 6; 9}, B = {0; 2; 4; 6; 8; 9} và C = {3; 4; 5; 6; 7}. Hãy tìm A ∩ (B \ C) và (A ∩ B) \ C. Hai tập hợp nhận được là bằng nhau hay khác nhau

Hướng dẫn giải: 

Ta có B \ C = {2; 0; 8; 9} nên A ∩ (B \ C) = {2; 9}. Mật khác, ta có A ∩ B = {2; 4; 6; 9} nên (A ∩ B) \ C = {2; 9}. Từ kết quả này ta thấy A ∩ (B \ C) = (A ∩ B) \ C.

---

Cho A và B là hai tập hợp. Dùng biểu đồ Ven để kiểm nghiệm rằng:

a) (A\B) ⊂ A;

b) A ∩ (B\ A) = Ø;

c) A ∪ (B\A) = A ∪ B.

Hướng dẫn giải:

---

Cho A là tập hợp các số tự nhiên chẵn không lớn hơn 10, B = {n ∈ N | n ≤ 6} và C = {n ∈ N| 4 < n < 10}. Hãy tìm:

a) A ∩ (B∪C);

b) (A \ B) ∪ (A \ C) ∪ (B \ C).

Hướng dẫn giải 

Ta có: A = {0; 2; 4; 6; 8; 10}, B = {0; 1; 2; 3; 4; 5; 6} và C = {4; 5; 6; 7; 8; 9; 10}.

Từ đó A ∩ (B ∪ C) = A và (A \ B) ∪ (A \ C) ∪ (B \ C) = {0; 1; 2; 3; 8; 10}.

---

Trong các cách viết sau đây cách viết nào đúng, cách viết nào sai:

a) a ⊂ {a; b}           Đúng             Sai 

b) {a} ⊂ {a; b}        Đúng             Sai 

Hướng dẫn giải 

a) Sai;

b) Đúng.

---

Cho tập hợp A = {a; b; c; d}. Liệt kê tất cả các tập con của A có:

a) Ba phần tử;

b) Hai phần tử;

c) Không quá một phần tử.

Hướng dẫn giải 

Câu a:

{a; b; c}, {a; b; d)}, {b; c; d}, {a; c; d}.

Câu b:

{a; b}, {a; c}, {a; d}, {b; c}, {b; d}, {c; d}.

Câu c:

Các tập con có không quá một phần tử là: {a}, {b}, {c}, {d}, Ø.

---

Cho A = [a; a + 2] và B = [b; b + 1]. Các số a, b cần thoả mãn điều kiện gì để A ∩ B ≠ Ø.

Hướng dẫn giải:

A ∩ B = 0 khi a + 2 < b hoặc b + 1 < a tức là a < b - 2 hoặc a > b + 1

Vậy A ∩ B ≠ Ø khi a ∈ [b - 2; b + 1].

---

Trong các khẳng định sau đây, khẳng định nào sai?

(A) Q ∩ R = Q;

(B) N* ∩ R = N*.

(C) X ∪ Q = Q.

(D) N ∪ N* = Z.

Hướng dẫn giải:

- Các khẳng định (A), (B), (C) là đúng vì ta dựa vào nhận xét A ⊂ B

⇒ A ∩ B = A.

- Khẳng định (D) là sai vì -1 ∈ Z nhưng - 1 ∉ N∪ N*.

(Chú ý là N ∪ N* = N).

---

Cho hai nửa khoảng A = (-1; 0] và B = [0; 1). Hãy tìm A ∪ B, A ∩ B và C_RA.

Hướng dẫn giải:

- Ta có: A ∪ B = {x ∈ R| -1 < x ≤ 0 hoặc 0 ≤ x < 1} = (-1; 1).

- Ta có: A ∩ B = (x ∈ R: -1 < x ≤ 0 và 0 ≤ x < 1} = {0}.

- C_RA = (-∞; -1] ∪ (0; +∞).

---

Cho A = {n ∈ Z| n = 2k, k ∈ Z}, B là tập hợp các số nguyên có số tận cùng là 0, 2, 4, 6, 8; C = {n ∈ Z | n = 2k - 2, k ∈ Z} và D = {n ∈ Z | n = 3k + 1, k ∈ Z}. Chứng minh rằng A = B, A = C và A ≠ D.

Hướng dẫn giải:

- Lấy x ∈ A ⇒ 3k₁ ∈ Z để x = 2k₁ ⇒ x là số chẵn hay x ∈ B.

Ngược lại, x ∈ B ⇒ tồn tại k₂ để x = 2k₂ với k - 2 ∈ Z ⇒ x ∈ A. Vậy A = B.

- Lấy x ∈ A => 3k₁ ∈ Z để x = 2k₁, đặt k₂ = k₁ - 1 ∈ Z ⇒ x = 2(k₂ - 1) ⇒ X ∈ C. Ngược lại, lấy x ∈ C ⇒ 3k₃ ∈ Z để x = 2k₃ - 2

hay x = 2(k₃ - 1), vì k₃ - 1 ∈ Z ⇒ x ∈ A. Vậy A = C.

- Với k = 2 ⇒ 3k + l = 7 ∉ A → A ≠ D.

---

Cho hai nửa khoảng A = (0; 2], B = [1; 4). Tìm CR (A ∪ B) và CR (A ∩ B).

Hướng dẫn giải:

- Ta có: A ∪ B = (0; 2] ∪ [1; 4) = (0; 4), từ đây suy ra:

C_R(A ∪ B) = (-∞; 0] ∪ [4; +∞).

- Ta có: A ∩ B = [1; 2], từ đây suy ra:

C_R(A ∩ B) = (-∞; 1) ∪ (2; +∞).

---

Cho A = {a; b; c}; B = {b; c; d}, c = {b; c; e}. Chọn khẳng định đúng trong các khẳng định sau:

(A) A ∪ (B∩C) = (A∪B) ∩ C.

(B) A ∪ (B∩C) = (A∪B) ∩ (A∪C).

(C) (A∪B) ∩ C = (A∪B) ∩ (A∪C)

(D) (A∩B) ∪ C = (A∪B) ∩ C.

Hướng dẫn giải:

Ta có: B ∩ C= {b; c}, A ∪ B = {a; b; c; d}, A ∪ C = {a; b; c; e}, A ∩ B = {b; c} nên:

- A ∪ (B∩C) = {a; b; c}, (A∪B) ∩ C= {b; c}

⇒ Khẳng định (A) là sai.

- A ∪ (B∩C) = {a; b; c}, (A∪B) ∩ (A∪C)= {a; b; c}

⇒ Khẳng định (B) là đúng.

- (A ∪ B) ∩ C = {b; c}, (A∪ B) ∩ (A∪ C)= {a; b ;c}

⇒ Khẳng định (C) là sai.

- (A∩B) ∪ C= {b; c; e}, (A∪B) ∩ C= {b; c}

⇒ Khẳng định (D) là sai.

 

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 1 Luyện tập (trang 21, 22) với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.