Giải Toán 10 SGK nâng cao Chương 2 Luyện tập (trang 45, 46, 47)

Quy tắc đặt tương ứng mỗi số thực dương với căn bậc hai của nó có phải là một hàm số không? Vì sao?

Hướng dẫn giải:

Quy tắc này không phải là một hàm số vì mỗi số thực dương có tới hai căn bậc hai phân biệt, như vậy vi phạm điều kiện duy nhất trong định nghĩa hàm số.

---

Giả sử (G) là đồ thị của hàm số y = f(x) xác định trên tập D; A là một điểm trên trục hoành có hoành độ bằng a. Từ A, dựng đường thẳng (d) song song (hoặc trùng) với trục tung.

a) Khi nào thì (d) có điểm chung với (G).

b) (d) có thể có bao nhiêu điểm chung với (G)? Vì sao?

c) Đường tròn có thể là đồ thị của hàm số không? Vì sao?

Hướng dẫn giải:

Câu a:

- (d) và (G) có điểm chung khi a ∈ D.

- (d) và (G) không có điểm chung khi a ∉ D.

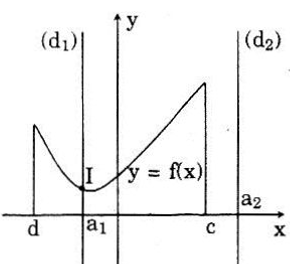
Hình vẽ bên minh họa cho trường hợp D = {d; c}. Trường hợp a = a₁ ∈ D, ta có (d₁) có giao điểm với (G) tại I.

Trường hợp a = a₂ ∉ D thì (d₂) và (G) không có giao điểm.

Câu b:

(d) và (G) có không quá một điểm chung, vì nếu trái lại, gọi M₁ và M₂ là hai điểm chung phân biệt thì ứng với a có tới hai giá trị của hàm số là các tung độ của điểm M₁, M₂. Trái với định nghĩa của hàm số.

Câu c:

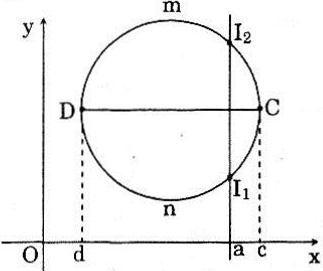
Đường tròn trong mặt phẳng tọa độ không là đồ thị của hàm số vì có đường thẳng song song với Oy cắt nó tại hai điểm phân biệt.

---

Tìm tập xác định của mỗi hàm số sau:

a) $y=\frac{3x+1}{x^2-9}$                            b) $y=\frac{x}{1-x^2}-\sqrt{-x}$

c) $y=\frac{x-3\sqrt{2-x}}{\sqrt{x+2}}$                     d) $y=\frac{\sqrt{x-1}+\sqrt{4-x}}{\left(x-2\right)\left(x-3\right)}$     

Hướng dẫn giải:

Câu a:

Biểu thức $\frac{3x+1}{x^2-9}$  có nghĩa khi và chỉ khi x² – 9 ≠ 0 ⇔ x ≠ 3 và x ≠ -3

=> Tập xác định của hàm số đã cho là R\ {3; -3}

Câu b:

Biểu thức $\frac{x}{1-x^2}-\sqrt{-x}$ có nghĩa ⇔ 1 – x² ≠ 0 và –x ≥ 0

⇔ x ≠ 1 và x ≠ -1 và x ≤ 0 ⇔ {x ≤ 0 và x ≠ -1} => Tập xác định của hàm số là $\left(-\mathrm{\infty };0\right]\mathrm{\setminus }\left\{-1\right\}$

Câu c:

Biểu thức $\frac{x-3\sqrt{2-x}}{\sqrt{x+2}}$ có nghĩa ⇔ {2 – x ≥ 0 và x + 2 > 0 } => - 2 ≤ x ≤ 2

=> Tập xác định của hàm số là : nửa khoảng (- 2; 2]

d)Tập xác định của hàm số là [1; 4) ∪ (2; 3) ∪ (3;4].

---

Cho hàm số 

$f\left(x\right)=\{\begin{array}{l}-2\left(x-2\right);-1\le x<1\\ \sqrt{x^2-1};x\ge 1\end{array}$

a) Tìm tập xác định của hàm số

b) Tính $f\left(-1\right);f\left(0,5\right);f\left(\frac{\sqrt{2}}{2}\right);f\left(1\right);f\left(2\right)$

Hướng dẫn giải:

Câu a:

Tập xác định của hàm số là $\left[-1;+\mathrm{\infty }\right)$

Câu b:

Ta có 

$\begin{array}{l}f\left(-1\right)=-2\left(-1-2\right)=6\\ f\left(0,5\right)=-2\left(0,5-2\right)=3\\ f\left(\frac{\sqrt{2}}{2}\right)=-2\left(\frac{\sqrt{2}}{2}-2\right)=-\sqrt{2}+4\\ f\left(1\right)=0\\ f\left(2\right)=\sqrt{3}\end{array}$

---

Trong các điểm A(- 2; 8); B(4;12), C(2;8) và $D\left(5;25+\sqrt{2}\right)$, điểm nào thuộc, điểm nào không thuộc đồ thị hàm số $f\left(x\right)=x^2+\sqrt{x-3}$? Vì sao?

Hướng dẫn giải:

Các điểm không thuộc đồ thị là A, B và C bởi vì :

$f\left(-2\right)\ne 8;f\left(4\right)\ne 12;f\left(2\right)\ne 8$

Điểm D thuộc đồ thị hàm số vì $f\left(5\right)=25+\sqrt{2}$

---

Khảo sát sự biến thiên của hàm số sau trên khoảng đã cho :

a) $y=\frac{1}{x-2}$ trên mỗi khoảng $\left(-\mathrm{\infty };2\right)$ và (2; + ∞ )

b) y = x² – 6x + 5 trên mỗi khoảng $\left(-\mathrm{\infty };3\right)$ và (3; + ∞)

c) y = x2005 + 1 trên khoảng (- ∞; + ∞ )

Hướng dẫn giải: 

Câu a:

$f\left(x\right)=\frac{1}{x-2}$

+ Với $x_1;x_2\in \left(-\mathrm{\infty };2\right)$ và $x_1\ne x_2$ ta có:

$\begin{array}{l}f\left(x_2\right)-f\left(x_1\right)=\frac{1}{x_2-2}-\frac{1}{x_1-2}=\frac{x_1-2-x_2+2}{\left(x_1-2\right)\left(x_2-2\right)}=\frac{x_1-x_2}{\left(x_1-2\right)\left(x_2-2\right)}\\ \Rightarrow \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}=\frac{-1}{\left(x_1-2\right)\left(x_2-2\right)}<0\end{array}$

Vậy hàm số $y=\frac{1}{x-2}$ nghịch biến trên $\left(-\mathrm{\infty };2\right)$

+ Với $x_1;x_2\in \left(2;+\mathrm{\infty }\right)$ và $x_1\ne x_2$ ta có:

$\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}=\frac{-1}{\left(x_1-2\right)\left(x_2-2\right)}<0$

Vậy hàm số $y=\frac{1}{x-2}$ nghịch biến trên $\left(2;+\mathrm{\infty }\right)$

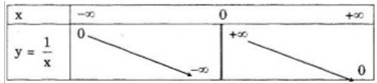
Bảng biến thiên

Câu b:

$f(x)=x^2-6x+5$

+ Với $x_1;x_2\in \left(-\mathrm{\infty };3\right)$ và $x_1\ne x_2$ ta có:

$f(x_2)–f(x_1)=x_2^2–6x_2+5–(x_1^2–6x_1+5)$

$=x_2^2-x_1^2+6(x_1–x_2)=(x_2–x_1)(x_1+x_2–6)$

$\Rightarrow \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}=x_1+x_2-6<0$ (vì $x_1<3;x_2<3$)

Vậy hàm số $y=x^2-6x+5$ nghịch biến trên $\left(-\mathrm{\infty };3\right)$

+ Với Với $x_1;x_2\in \left(3;+\mathrm{\infty }\right)$ và $x_1\ne x_2$ ta có:

$\Rightarrow \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}=x_1+x_2-6>0$ (vì $x_1>3;x_2>3$

Vậy hàm số $y=x^2-6x+5$ đồng biến trên $\left(3;+\mathrm{\infty }\right)$

Bảng biến thiên

Câu c:

Với mọi $x_1;x_2\in \left(-\mathrm{\infty };+\mathrm{\infty }\right)$ ta có $x_1<x_2$

$\begin{array}{l}\Rightarrow {x_1}^{2005}<x_2^{2005}\\ \Rightarrow {x_1}^{2005}+1<x_2^{2005}+1\end{array}$

hay $f\left(x_1\right)<f\left(x_2\right)\left(y=f\left(x\right)=x^{2005}+1\right)$

Vậy hàm số đã cho đồng biến trên $\left(-\mathrm{\infty };+\mathrm{\infty }\right)$

---

Hàm số $y=\frac{1}{x}$ có đồ thị như hình 2.10

a) Dựa vào đồ thị, hãy lập bảng biến thiên của hàm số đó

b) Bằng tính toán, hãy khảo sát sự biến thiên của hàm số trên khoảng $\left(-\mathrm{\infty };0\right)$ và $\left(0;+\mathrm{\infty }\right)$ và kiểm tra lại kết quả so với bảng biến thiên đã lập

 

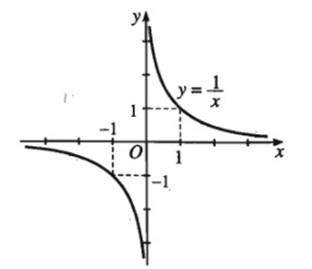
Hướng dẫn giải: 

Câu a:

Bảng biến thiên của hàm số

 

Câu b:

Với $x_1,x_2\in \left(-\mathrm{\infty };0\right)$ và $x_1\ne x_2$ ta có:

$\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}=\frac{\frac{1}{x_2}-\frac{1}{x_1}}{x_2-x_1}=\frac{-1}{x_1{x}_2}<0$ (vì $x_1<0;x_2<0$)

Vậy hàm số $y=\frac{1}{x}$ nghịch biến trên $\left(-\mathrm{\infty };0\right)$

Tương tự hàm số $y=\frac{1}{x}$ cũng nghịch biến trên $\left(0;+\mathrm{\infty }\right)$ 

Tập con S của tập số thực $\mathbb{R}$ gọi là đối xứng nếu mọi x thuộc S, ta đều có – x thuộc S. Em có nhận xét gì về tập xác định của một hàm số chẵn (lẻ).

Từ nhận xét đó, em có kết luận gì về tính chẵn – lẻ của hàm số $y=\sqrt{x}$? Tại sao?

Hướng dẫn giải:

Tập xác định của một hàm số chẵn (lẻ) là tập đối xứng.

Hàm số $y=\sqrt{x}$$\sqrt{}$ không là hàm số chẵn, cũng không là hàm số lẻ vì tập xác định của nó là $D=\left[0;+\mathrm{\infty }\right)$ không phải là tập đối xứng (do 1 ∈ D nhưng -1 ∉ D).

Gọi (d) là đường thẳng y = 2x và (d’) là đường thẳng y = 2x–3. Ta có thể coi (d’) có được là do tịnh tiến (d):

a) Lên trên hay xuống dưới bao nhiêu đơn vị?

b) Sang trái hay sang phải bao nhiêu đơn vị?

Hướng dẫn giải:

Câu a:

(d’) có được là do tịnh tiến xuống dưới 3 đơn vị

Câu b:

Ta có:

$y=2x-3=2\left(x-\frac{3}{2}\right)$

Vậy (d’) có được là do tịnh tiến (d) sang phải $\frac{3}{2}$ đơn vị.

---

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 2 Luyện tập (trang 45, 46, 47) với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.