Bài 1 trang 44 SGK Toán 10 nâng cao
Tìm tập xác định của hàm số sau:
a) \(y = \frac{{3x + 5}}{{{x^2} - x + 1}}\); b) \(y = \frac{{x - 2}}{{{x^2} - 3x + 2}}\);
c) \(y = \frac{{\sqrt {x - 1} }}{{x - 2}}\); d) \(y = \frac{{{x^2} - 2}}{{\left( {x + 2} \right)\sqrt {x + 1} }}\)
Hướng dẫn giải:
Câu a:
Do phương trình x2 - x + 1 = 0 vô nghiệm nên x2 - x + 1 ≠ 0, ∀ x ∈ R. Từ đây ta suy ra tập xác định của hàm số là R.
Câu b:
Ta có phương trình: x2 - 3x + 2 = 0 có tập nghiệm là {1; 2}. Từ đây ta suy ra: x2 - 3x + 2 ≠ 0 ⇔ x ∈ R \ {1; 2}. Vậy tập xác định của hàm số là R \ {1; 2}.
Câu c:
Biểu thức \(\frac{{\sqrt {x - 1} }}{{x - 2}}\) có nghĩa khi và chỉ khi x – 1 ≥ 0 và x – 2 ≠ 0 hay x ≥ 1 và x ≠ 2. Vậy tập xác định của hàm số là : [1; 2) ∪ (2; +∞).
Câu d:
Biểu thức có nghĩa khi và chỉ khi x + 2 ≠ 0 và x + 1 > 0 ⇔ x ≠ 2 và x > -1 ⇔ x > -1
Vậy tập xác định của hàm số là ( - 1; +∞)
Bài 2 trang 44 SGK Toán 10 nâng cao
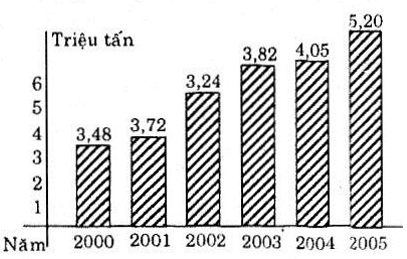
Biểu đồ ở hình bên cho biết số triệu tấn gạo xuất khẩu của Việt Nam trong các năm từ 2000 đến 2005. Biểu đồ này cho một hàm số. Hãy cho biết tập xác định và nêu một vài giá trị của hàm số đó
Hướng dẫn giải:
Ta gọi hàm số là f(x). Khi đó, tập xác định của hàm là : {2000; 2001; 2002; 2003; 2004; 2005}. Ta tính được:
f(2000) = 3,48; f(2001) = 3,72;
f(2002) = 3,24; f(2003) = 3,82;
f(2004) = 4,05; f(2005) = 5,20.
Bài 3 trang 45 SGK Toán 10 nâng cao
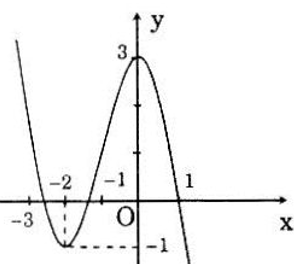
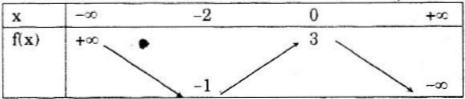
Hình bên là đồ thị của một hàm số có tập xác định là R. Dựa vào đồ thị hãy lập bảng biến thiên của hàm số
Hướng dẫn giải:
Bảng biến thiên :
Bài 4 trang 45 SGK Toán 10 nâng cao
Khảo sát sự biến thiên của mỗi hàm số sau và lập bảng của nó:
a) \(y = x^2 + 2x - 2\) trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\);
b) \(y = - 2x^2 + 4x + 1\) trên mỗi khoảng \(\left( { - \infty ; -1} \right)\) và \(\left( { 1; + \infty } \right)\);
c) \(y = \frac{2}{{x - 3}}\) trên mỗi khoảng \(\left( { - \infty ; 3} \right)\) và \(\left( { 3; + \infty } \right)\)
Hướng dẫn giải:
Câu a:
Ta có :
+ Với mọi \({x_1};{x_2} \in \left( { - \infty ; - 1} \right)\) và \({x_1} \ne {x_2}\) ta có:
\(f(x_2) – f(x_1) = x_2^2 + 2x_2 – 2 – (x_1^2 + 2x_1 – 2)\)
\(= x_2^2 – x_1^2 + 2(x_2 – x_1) = (x_2 – x_1)(x_1 + x_2 + 2)\)
\( \Rightarrow \frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = {x_1} + {x_2} + 2\)
Vì \(x_1<-1\) và \(x_2<-1\) nên \(x_1+x_2+2<0\) nên \(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} < 0\)
Vậy hàm số \(y=x^2+2x-2\) nghịch biến trên \(\left( { - \infty ; - 1} \right)\)
+ Với mọi \({x_1};{x_2} \in \left( { - 1; + \infty } \right)\) và \({x_1} \ne {x_2}\) ta có:
\(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = {x_1} + {x_2} + 2 > 0\) (vì \(x_1>-1; x_2>-1\)
Câu b:
Ta có :
+ Với mọi \({x_1};{x_2} \in \left( { - \infty ; 1} \right)\) và \({x_1} \ne {x_2}\) ta có:
\(f(x_2) – f(x_1) = (-2x_2^2 + 4x_2 + 1) – (-2x_1^2 + 4x_1 + 1)\)
\(= -2(x_2^2 - x_1^2) + 4(x_2 - x_1) = 2(x_2 - x_1)(2 – x_1 – x_2)\)
\( \Rightarrow \frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = 2\left( {2 - {x_1} - {x_2}} \right)\)
Vì \(x_1 < 1\) và \(x_2 < 1\) nên \(2 - x_1 – x_2 > 0\)
Vậy hàm số \(y = -2x^2 + 4x + 1\) đồng biến trên khoảng \(\left( { - \infty ;1} \right)\)
+ Với mọi \({x_1};{x_2} \in \left( { 1; + \infty } \right)\) và \({x_1} \ne {x_2}\) ta có:
\(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = 2\left( {2 - {x_1} - {x_2}} \right) < 0\) (vì \(x_1>1\) và \(x_2>1\))
Vậy hàm số \(y=-2x^2+4x+1\) nghịch biến trên khoảng \(\left( {1; + \infty } \right)\)
Câu c:
Ta có :
+ Với mọi \({x_1};{x_2} \in \left( { - \infty ; 3} \right)\) và \({x_1} \ne {x_2}\) ta có:
\(\begin{array}{l}
f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = \frac{2}{{{x_2} - 3}} - \frac{2}{{{x_1} - 3}}\\
= \frac{{2\left( {{x_1} - 3} \right) - 2\left( {{x_2} - 3} \right)}}{{\left( {{x_1} - 3} \right)\left( {{x_2} - 3} \right)}} = \frac{{2\left( {{x_1} - {x_2}} \right)}}{{\left( {{x_1} - 3} \right)\left( {{x_2} - 3} \right)}}
\end{array}\)
\( \Rightarrow \frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \frac{{ - 2}}{{\left( {{x_1} - 3} \right)\left( {{x_2} - 3} \right)}}\) (vì \(x_1<3; x_2<3\) nên \((x_1-3)(x_2-3)>0\))
\( \Rightarrow \frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} < 0\)
Vậy hàm số \(y = \frac{2}{{x - 3}}\) nghịch biến trên \(\left( { - \infty ;3} \right)\)
+ Với mọi \({x_1};{x_2} \in \left( { 3; + \infty } \right)\) và \({x_1} \ne {x_2}\) ta có:
\(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \frac{{ - 2}}{{\left( {{x_1} - 3} \right)\left( {{x_2} - 3} \right)}} < 0\) (vì \(x_1 > 3; x_2 > 3\) nên \((x_1 – 3)(x_2 – 3) > 0\))
Vậy hàm số \(y = \frac{2}{{x - 3}}\) nghịch biến trên \(\left( {3; + \infty } \right)\)
Bài 5 trang 45 SGK Toán 10 nâng cao
Mỗi hàm số sau là hàm số chẵn hay hàm số lẻ?
a) y = x4 – 3x2 + 1
b) y = - 2x3 + x
c) y = |x + 2| - |x – 2|
d) y = |2x + 1| + |2x – 1|
Hướng dẫn giải:
Câu a:
f(x) = x4 – 3x2 + 1
Với mọi x ∈ R thì – x ∈ R
Và f(- x) = (-x)4 – 3(-x)2 + 1 = x4 – 3x2 + 1 = f(x)
⇒ y = x4 – 3x2 + 1 là hàm số chẵn
Câu b:
f(x) = - 2x3 + x
Với mọi x ∈ R thì – x ∈ R
Và f(-x) = - 2(- x)3 + (-x) = - (- 2x3 + x) = - f(x)
⇒ y = - 2x3 + x là hàm số lẻ
Câu c:
f(x) = |x + 2| - |x – 2|
Với mọi x ∈ R thì – x ∈ R
Và f(-x) = |-x + 2| - |- x – 2| = |x – 2| - |x + 2| = - f(x)
⇒ y = |x + 2| - |x – 2| là hàm số lẻ
Câu d:
f(x) = |2x + 1| + |2x – 1|
Với mọi x ∈ R thì – x ∈ R
Và f(- x) = |- 2x + 1| + |- 2x – 1| = |2x – 1| + |2x + 1| = f(x)
⇒ y = |2x + 1| + |2x – 1| là hàm số chẵn
Bài 6 trang 45 SGK Toán 10 nâng cao
Cho đường thẳng (d): y = 0,5x. Hỏi ta sẽ được đồ thị của hàm số nào khi tịnh tiến (d):
a) Lên trên 3 đơn vị
b) Xuống dưới 1 đơn vị
c) Sang phải 2 đơn vị
d) Sang trái 6 đơn vị
Hướng dẫn giải:
Câu a:
Tịnh tiến (d) lên trên 3 đơn vị ta được đồ thị hàm số y = 0,5x + 3
Câu b:
Tịnh tiến (d) xuống dưới 1 đơn vị, ta được đồ thị hàm số y = 0,5x – 1
Câu c:
Tịnh tiến (d) sang phải 2 đơn vị, ta được đồ thị hàm số y = 0,5 (x – 2) hay y = 0,5x - 1
Câu d:
Tịnh tiến (d) sang trái 6 đơn vị, ta được đồ thị hàm số y = 0,5(x + 6) hay y = 0,5x +3
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 2 Bài 1 Đại cương về hàm số với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.
