Giải Toán 10 SGK nâng cao Chương 2 Bài 2 Hàm số bậc nhất

Tìm các cặp đường thẳng song song trong các đường thẳng sau:

a) \(y = \frac{1}{{\sqrt 2 }}x + 1\)

b) \(y =  - \frac{1}{{\sqrt 2 }}x + 3\)

c) \(y = \frac{2}{{\sqrt 2 }}x + 2\)

d) \(y = \sqrt 2 x - 2\)

e) \(y = \frac{1}{{\sqrt 2 }}x - 1\)

f) \(y =  - \left( {\frac{{\sqrt 2 }}{2}x - 1} \right)\)

Hướng dẫn giải:

Các cặp đường thẳng song song là:

(d1): \(y = \frac{1}{{\sqrt 2 }}x + 1\) và (d2): \(y = \frac{1}{{\sqrt 2 }}x - 1\)

(d3): \(y = \frac{2}{{\sqrt 2 }}x + 2\) và (d4): \(y = \sqrt 2 x - 2\)

(d5): \(y =  - \frac{1}{{\sqrt 2 }}x + 3\) và (d6): \(y =  - \left( {\frac{{\sqrt 2 }}{2}x - 1} \right)\)

Cho hàm số:

\(y = f\left( x \right) = \left\{ \begin{array}{l}
2x + 4,\,\,\,\, - 2 \le x <  - 1\\
 - 2x,\,\,\,\,\,\,\,\, - 1 \le x \le 1\\
x - 3,\,\,\,\,\,\,\,1 < x \le 3
\end{array} \right.\)

a) Tìm tập xác định và vẽ đồ thị của hàm số đó

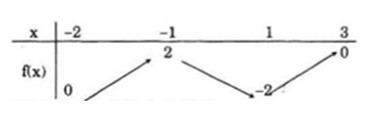
b) Cho biết sự biến thiên của hàm số đã cho trên mỗi khoảng (- 2;- 1); (- 1;1) và (1;3) và lập bảng biến thiên của nó.

Hướng dẫn giải: 

Câu a:

Tập xác định của hàm số: D = [- 2;3]

Bảng giá trị 

Đồ thị hàm số 

Câu b:

Hàm số đồng biến trên khoảng (-2; -1); nghịch biến trên khoảng (-1; -1) và đồng biến trên khoảng (1; 3)

Bảng biến thiên của hàm số

b) Cho phép tịnh tiến biến đồ thị hàm số \(f_1\) thành đồ thị hàm số \(f_2\)

Hướng dẫn giải:

Câu a:

Ta có:

 \(\begin{array}{l}
y = {f_1}\left( x \right) = \left\{ \begin{array}{l}
2x,\,\,\,\,x \ge 0\\
 - 2x,\,x < 0
\end{array} \right.\\
y = {f_2}\left( x \right) = \left\{ \begin{array}{l}
2x + 5,\,\,\,\,\,\,x \ge  - \frac{5}{2}\\
 - 2x - 5,\,\,\,x <  - \frac{5}{2}
\end{array} \right.
\end{array}\)

Bảng giá trị 

Đồ thị hàm số 

Câu b:

Tịnh tiến đồ thị hàm số \(f_1\) sang trái \(\frac{5}{2}\) đơn vị, ta được đồ thị hàm số \(f_2\)

Thật vậy, ta có:

\({f_1}\left( {x + \frac{5}{2}} \right) = 2\left| {x + \frac{5}{2}} \right| = \left| {2\left( {x + \frac{5}{2}} \right)} \right| = {f_2}\left( x \right)\)

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 2 Bài 2 Hàm số bậc nhất với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.