Giải Toán 10 SGK nâng cao Chương 4 Bài 6 Dấu của tam thức bậc hai

Xét dấu các tam thức bậc hai sau:

a) 3x² - 2x + 1

b) - x² + 4x – 1

c) $x^2-\sqrt{3}x+\frac{3}{4}$

d) $\left(1-\sqrt{2}\right)x^2-2x+1+\sqrt{2}$

Hướng dẫn giải:

Câu a:

Ta có:

a = 3 > 0

Δ’ = 1 – 3 = - 2 < 0

⇒ 3x² – 2x + 1 > 0, ∀x  ∈ R

Câu b:

Đặt f(x) = - x2 + 4x – 1

Ta có:

a = -1 < 0

Δ’ = 4 – 1 = 3 > 0

Tam thức - x² + 4x – 1 có hai nghiệm phân biệt $x=2\pm \sqrt{3}$

Bảng xét dấu

                     

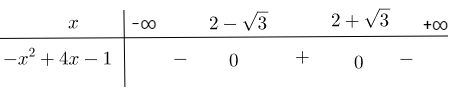
Vậy f(x) > 0 với mọi $x\in \left(2-\sqrt{3};2+\sqrt{3}\right)$

f(x) < 0 với mọi $x\in \left(-\mathrm{\infty };2-\sqrt{3}\right)\cup \left(2+\sqrt{3};+\mathrm{\infty }\right)$

Câu c:

Ta có:

a = 1 > 0

Δ = 3 – 3 = 0

 $x^2-\sqrt{3}x+\frac{3}{4}$ có nghiệm kép là $x=\frac{\sqrt{3}}{2}$

Suy ra $x^2-\sqrt{3}x+\frac{3}{4}>0,\mathrm{\forall }x\ne \frac{\sqrt{3}}{2}$

Câu d:

Đặt f(x) = $\left(1-\sqrt{2}\right)x^2-2x+1+\sqrt{2}$

$\begin{array}{l}a=1-\sqrt{2}<0\\ \left(1-\sqrt{2}\right)x^2-2x+1+\sqrt{2}=0\iff [\begin{array}{c}x=1\\ x=-3-2\sqrt{2}\end{array}\end{array}$

Bảng xét dấu

Vậy f(x) > 0 với mọi $x\in \left(-3-2\sqrt{3};1\right)$

f(x) < 0 với mọi $\left(-\mathrm{\infty };-3-2\sqrt{3}\right)\cup \left(1;+\mathrm{\infty }\right)$

---

Tìm các giá trị của m để mỗi biểu thức sau luôn dương:

a) (m²+2)x² - 2(m+1)x + 1

b) (m+2)x² + 2(m+2)x + m + 3

Hướng dẫn giải:

Câu a:

Vì m² + 2 > 0 nên (m²+2)x² - 2(m+1)x + 1 > 0, ∀x ∈ R

⇔ Δ’ = (m + 1)² – (m² + 2) < 0 ⇔ 2m – 1 < 0

⇔ $m<\frac{1}{2}$

Vậy với $m<\frac{1}{2}$ thì (m²+2)x² - 2(m+1)x + 1 > 0, ∀ x ∈ R

Câu b:

• Với m = - 2 thì $f\left(x\right)=1>0,\mathrm{\forall }x\in R$
• Với $m\ne -2$ ta có $f\left(x\right)>0,\mathrm{\forall }x\in R$

$\begin{array}{l}\iff \{\begin{array}{c}a>0\\ {\mathrm{\Delta }}^{\prime }<0\end{array}\iff \{\begin{array}{c}m+2>0\\ {\left(m+2\right)}^2-\left(m+2\right)\left(m+3\right)<0\end{array}\\ \iff \{\begin{array}{c}m>-2\\ -m-2<0\end{array}\iff m>-2\end{array}$

Vậy $f\left(x\right)>0,\mathrm{\forall }x\in R\iff m\ge -2$

---

Tìm các giá trị của m để mỗi biểu thức sau luôn âm.

a) $-x^2+2m\sqrt{2}x-2m^2-1$

b) $\left(m-2\right)x^2-2\left(m-3\right)x+m-1$

Hướng dẫn giải:

Câu a:

Vì a = - 1 < 0 nên:

$\begin{array}{l}-x^2+2m\sqrt{2}x-2m^2-1<0,\mathrm{\forall }x\in R\\ \iff {\mathrm{\Delta }}^{\prime }=2m^2-\left(2m^2+1\right)<0\\ \iff -1<0\left(ld\right)\end{array}$

Vậy với mọi m thì $-x^2+2m\sqrt{2}x-2m^2-1<0,\mathrm{\forall }x\in R$

Câu b:

Đặt $f\left(x\right)=\left(m-2\right)x^2-2\left(m-3\right)x+m-1$

Với m = 2 thì $f(x)=2x+1$ không thỏa mãn điều kiện yêu cầu bài toán.

Với $m\ne 2$ thì $f\left(x\right)<0,\mathrm{\forall }x\in R$

$\begin{array}{l}\iff \{\begin{array}{c}a<0\\ {\mathrm{\Delta }}^{\prime }<0\end{array}\\ \iff \{\begin{array}{c}m-2<0\\ {\left(m-3\right)}^2-\left(m-2\right)\left(m-1\right)<0\end{array}\\ \iff \{\begin{array}{c}m<2\\ -3m+7<0\end{array}\iff \{\begin{array}{c}m<2\\ m>\frac{7}{3}\end{array}\end{array}$

Ta không tìm được m thỏa mãn hệ thức trên.

Vậy không có giá trị m để $f\left(x\right)<0,\mathrm{\forall }x\in R$

---

Chứng minh định lý về dấu của tam thức bậc 2.

Hướng dẫn: Với các trường hợp Δ < 0 và Δ = 0, sử dụng hệ thức đã biết:

$f\left(x\right)=a\left[{\left(x+\frac{b}{2a}\right)}^2-\frac{\mathrm{\Delta }}{4a^2}\right]$

Hay $af\left(x\right)=a^2\left[{\left(x+\frac{b}{2a}\right)}^2-\frac{\mathrm{\Delta }}{4a^2}\right]$

Trong trường hợp Δ > 0, sử dụng hệ thức đã biết:

f(x) = a(x – x₁)(x – x₂) hay af(x) = a²(x – x₁)(x – x₂)

trong đó x₁ và x₂ là hai nghiệm của tam thức bậc hai f(x)

Hướng dẫn giải:

Ta có: $af\left(x\right)=a^2\left[{\left(x+\frac{b}{2a}\right)}^2-\frac{\mathrm{\Delta }}{4a^2}\right]$

• Nếu Δ < 0 thì af(x) > 0 với mọi x ∈ R, tức f(x) cùng dấu với a với mọi x ∈ R
• Nếu Δ = 0 thì $af\left(x\right)=a^2{\left(x+\frac{b}{2a}\right)}^2$ khi đó af(x) > 0 với mọi $x\ne -\frac{b}{2a}$
• Nếu Δ > 0 thì f(x) có hai nghiệm phân biệt x₁ và x₂ và f(x) = a(x – x₁)(x – x₂)

Do đó: af(x) = a²(x – x₁)(x – x₂)

Vậy af(x) có cùng dấu với tích (x – x₁)(x – x₂).

Dấu của tích này được cho trong bảng sau (x₁ < x₂)

 

Do đó: af(x) < 0 với mọi x ∈ (x₁, x₂)

Và af(x) > 0 với mọi x < x₁ hoặc x > x₂