Giải Toán 10 SGK nâng cao Chương 2 Bài 3 Hệ thức lượng trong tam giác

Tam giác ABC có a = 12, b = 13, c = 15. Tính cosA và gócA.

Hướng dẫn giải:

Áp dụng công thức tính  ta có 

$\begin{array}{l}\cos A=\frac{b^2+c^2-a^2}{2bc}=\frac{{13}^2+{15}^2-{12}^2}{2.13.15}=\frac{25}{39}\\ \Rightarrow \hat{A}\approx {50}^0\end{array}$

---

Cho tam giác ABC có AB = 5, AC = 8, góc A = 60⁰. Kết quả nào trong các kết quả sau là độ dài cạnh BC?

a) $\sqrt{129}$;                                            b) 7;

c) 49;                                                  d) $\sqrt{69}$.

Hướng dẫn giải:

Ta có BC² = a² = b²+c²−2bc.cosA = 8²+5²−2.8.5.cos60⁰ = 49

⇒BC = 7.

Chọn b).

---

Hình 59 vẽ một hồ nước nằm ở góc tạo bởi hai con đường. Bốn bạn An, Cường , Trí, Đức dự đoán khoảng cách từ B đến C như sau

An :         5km

Cường :   6km

Trí :         7km

Đức :       5,5km

Biết rằng khoảng cách từ A đến B là 3km, khoảng cách từ A đến C là 4km, góc BAC là 120⁰.

Hỏi dự đoán của bạn nào sát với thực tế nhất ?

Hướng dẫn giải:

Áp dụng định lí cosin ta có

BC² = AB²+AC²−2AB.AC.cos BAC = 3²+4²−2.3.4.cos120⁰ = 9+16+12 = 37

$\Rightarrow BC=\sqrt{37}\approx 6,1$

Vậy bạn Cường dự đoán sát với thực tế  nhất.

---

Cho tam giác ABC. Chứng minh các khẳng định sau

a) Góc A nhọn khi và chỉ khi a² < b²+c²;

a) Góc A tù khi và chỉ khi a² > b²+c²;

a) Góc A vuông khi và chỉ khi a² = b²+c².

Hướng dẫn giải:

Ta có $\cos A=\frac{b^2+c^2-a^2}{2bc}$

a) A nhọn ⇔ cosA > 0 ⇔ b²+c² > a².

b) A tù ⇔ cosA < 0 ⇔ b²+c² < a².

c) A vuông ⇔ cosA = 0 ⇔ b²+c² = a².

---

Tam giác ABC có $\hat{A}={60}^0,\hat{B}={45}^0,b=4$. Tính hai cạnh a và c.

Hướng dẫn giải:

Ta có $\hat{C}={180}^0-\hat{A}-\hat{B}={180}^0-{60}^0-{45}^0={75}^0$

Áp dụng định lý sin ta có:

$\begin{array}{l}\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin c}=\frac{4}{\sin {45}^0}\\ \frac{a}{\sin {60}^0}=\frac{4}{\sin {45}^0}\Rightarrow a=4.\frac{\sqrt{3}}{2}.\sqrt{2}=2\sqrt{6}\\ \frac{c}{\sin {75}^0}=\frac{4}{\sin {45}^0}\Rightarrow c\approx 5,5\end{array}$

---

Cho tam giác ABC có góc A = 60⁰, a = 6. Tính bán kính đường tròn ngoại tiếp tam giác.

Hướng dẫn giải:

Ta có: $\frac{a}{\sin A}=2R\Rightarrow R=\frac{a}{2\sin A}=\frac{6}{2\sin {60}^0}=\frac{6}{\sqrt{3}}=2\sqrt{3}\approx 3,5$

---

Chứng minh rằng nếu ba góc của tam giác ABC thỏa mãn hệ thức sinA = 2sinB.cosC thì ABC là tam giác cân.

Hướng dẫn giải:

Áp dụng định lí sin và cosin ta có

$\sin A=\frac{a}{2R},\sin B=\frac{b}{2R},cosC=\frac{a^2+b^2-c^2}{2bc}$

Do đó 

$\begin{array}{l}\sin A=2\sin B\cos C\iff \frac{a}{2R}=2.\frac{b}{2R}.\frac{a^2+b^2-c^2}{2ab}\\ \iff a^2=a^2+b^2-c^2\iff b^2=c^2\iff b=c\end{array}$

Vậy ABC là tam giác cân.

---

Hình 60 vẽ một chiếc tàu thủy đang neo đậu ở vị trí C trên biển và hai người ở các vị trí quan sát A và B cách nhau 500m. Họ đo được góc CAB bằng 87⁰ và góc CBA bằng 62⁰.

Tính các khoảng cách AC và BC.

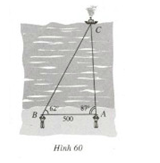
Hướng dẫn giải:

Ta có ACB = 180⁰−87⁰−62⁰ = 31⁰

Áp dụng định lí sin ta có:

$\begin{array}{l}\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=\frac{500}{\sin {31}^0}\approx 971\\ \Rightarrow BC=a=971.\sin {87}^0\approx 969m,AC=b=971.\sin {62}^0\approx 857m\end{array}$

---

Gọi H là trực tâm của tam giác không vuông ABC. Chứng minh rằng bán kính các đường tròn ngoại tiếp các tam giác ABC, HBC, HCA, HAB bằng nhau.

Hướng dẫn giải:

Trường hợp 1: Tam giác ABC có ba góc nhọn.

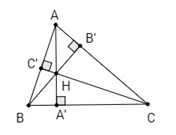
Gọi R, R₁ lần lượt là bán kính đường tròn ngoại tiếp tam giác ABC, HBC.

Áp dụng định lí sin ta có

$\frac{BC}{\sin A}=2R;\frac{BC}{\sin \widehat{BHC}}=2R_1$

Mà $\widehat{BHC}+\hat{A}=\widehat{B^{\prime }H{C}^{\prime }}+\hat{A}={180}^0$ (Vì 2 góc BHC và B′HC′ đối đỉnh)

⇒ sinA = sinBHC

Do đó  2R = 2R₁ ⇒ R = R₁.

Vậy bán kính đường tròn ngoại tiếp tam giác HBC bằng bán kính đường tròn ngoại tiếp tam giác ABC.

Tương tự bán kính đường tròn ngoại tiếp tam giác HCA, HAB bằng bán kính đường tròn ngoại tiếp tam giác ABC.

Trường hợp 2: Tam giác ABC có góc tù.

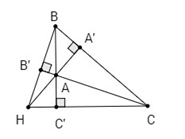
Ta có $\frac{BC}{\sin \widehat{BAC}}=2R;\frac{BC}{\sin \widehat{BHC}}=2R_1$

Mà $\widehat{B^{\prime }A{C}^{\prime }}+\widehat{CHB}={180}^0\sin \widehat{BAC}=\sin \widehat{B^{\prime }A{C}^{\prime }}=\sin \widehat{CHB}$ (Vì BAC và B′AC′ đối đỉnh)

⇒ R = R₁ 

Tương tự ta chứng minh được bán kính đường tròn ngoại tiếp tam giác HCA, HAB bằng bán kính đường tròn ngoại tiếp tam giác ABC.

---

Tam giác ABC có a = 7,b = 8,c = 6. Tính m_a.

Hướng dẫn giải:

Áp dụng công thức tính m_a ta có:

$m_a^2=\frac{b^2+c^2}{2}-\frac{a^2}{4}=\frac{8^2+6^2}{2}-\frac{7^2}{4}=\frac{151}{4}\Rightarrow m_a\approx 6,1$

---

Tam giác ABC có a = 5, b = 4, c = 3. Lấy điểm D đối xứng với B qua C. Tính độ dài AD.

Hướng dẫn giải:

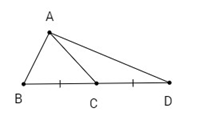
Áp dụng công thức tính trung tuyến AC trong tam giác ABD ta có:

$\begin{array}{l}A{C}^2=\frac{A{B}^2+A{D}^2}{2}-\frac{B{D}^2}{4}\Rightarrow 4^2=\frac{3^2+A{D}^2}{2}-\frac{{10}^2}{4}\\ \Rightarrow A{D}^2=73\Rightarrow AD=\sqrt{73}\approx 8,5\end{array}$

---

Cho hình bình hành ABCD có AB = 4, BC = 5, BD = $7$. Tính AC.

Hướng dẫn giải:

 

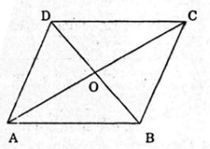
Gọi O là tâm hình bình hành.

Áp dụng công thức tính trung tuyến $AO$ của tam giác $ABD$, ta có:

$\begin{array}{l}A{O}^2=\frac{A{B}^2+A{D}^2}{2}-\frac{B{D}^2}{4}=\frac{4^2+5^2}{2}-\frac{7^2}{4}=\frac{33}{4}\\ \Rightarrow AO=\sqrt{\frac{33}{4}}=\frac{\sqrt{33}}{2}\\ \Rightarrow AC=2AO=\sqrt{33}\approx 5,8\end{array}$

---

Chứng minh rằng trong một hình bình hành, tổng bình phương các cạnh bằng tổng bình phương của hai đường chéo.

Hướng dẫn giải:

Áp dụng công thức tính trung tuyến AO trong tam giác ABD, ta có:

$\begin{array}{l}A{O}^2=\frac{A{B}^2+A{D}^2}{2}-\frac{B{D}^2}{4}\\ \iff 4A{O}^2=2\left(A{B}^2+A{D}^2\right)-B{D}^2\\ \iff A{C}^2+B{D}^2=2\left(A{B}^2+A{D}^2\right)=A{B}^2+A{D}^2+D{C}^2+B{C}^2\end{array}$

---

Chứng minh rằng tam giác ABC vuông ở A khi và chỉ khi 5m²_a = m²_b+m²_c.

Hướng dẫn giải:

Ta có 5m²_a = m²_b+m²_c

$\begin{array}{l}\iff 5\left(\frac{b^2+c^2}{4}-\frac{a^2}{4}\right)=\frac{a^2+c^2}{2}-\frac{b^2}{4}+\frac{a^2+b^2}{2}-\frac{c^2}{4}\\ \iff 5\left(2b^2+2c^2-a^2\right)=2a^2+2c^2-b^2+2a^2+2b^2-c^2\\ \iff b^2+c^2=a^2\end{array}$

Suy ra tam giác ABC vuông ở A.

---

Tam giác ABC có b = 6,12; c = 5,35; A = 84⁰. Tính diện tích tam giác đó.

Hướng dẫn giải:

Ta có $S_{ABC}=\frac{1}{2}bc\sin A=\frac{1}{2}.6,12.5,35.sin{84}^0\approx 16,3$

---

Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AC và BD. Chứng minh rằng AB²+BC²+CD²+DA² = AC²+BD²+4MN².

Hướng dẫn giải:

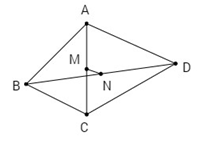
Áp dụng công thức tính trung tuyến, MN là trung tuyến của tam giác BMD, ta có:

$M{N}^2=\frac{B{M}^2+D{M}^2}{2}-\frac{B{D}^2}{4}\iff 4M{N}^2=2\left(B{M}^2+D{M}^2\right)-B{D}^2\left(1\right)$

Tương tự, BM, DM lần lượt là trung tuyến của tam giác ABC, ADC nên:

$\begin{array}{l}4B{M}^2=2\left(A{B}^2+B{C}^2\right)-A{C}^2\left(2\right)\\ 4D{M}^2=2\left(D{A}^2+C{D}^2\right)-A{C}^2\left(3\right)\end{array}$

Từ (2), (3) suy ra:

$2\left(B{M}^2+D{M}^2\right)=A{B}^2+B{C}^2+C{D}^2+D{A}^2-A{C}^2\left(4\right)$

Thay (4) vào (1), ta có

4MN² = AB²+BC²+CD²+DA²−AC²−BD² ⇒ AB²+BC²+CD²+DA² = AC²+BD²+4MN²

---

Gọi S là diện tích và R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứng minh rằng S = 2R²sinAsinBsinC.

Hướng dẫn giải:

Áp dụng công thức tính diện tích và định lí sin trong tam giác ABC .Ta có:

$S=\frac{abc}{4R}=\frac{\left(2R\sin A\right)\left(2R\mathrm{sinB}\right)\left(2R\mathrm{sinC}\right)}{4R}=2R^2\sin A\sin B\sin C$

---

Chứng minh rằng diện tích của một tứ giác bằng nửa tích hai đường chéo và sin của góc hợp bởi hai đường chéo đó.

Hướng dẫn giải:

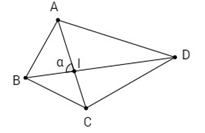
Gọi I là giao điểm của hai đường chéo AC,BD và AIB = α.

Ta có $S_{ABI}=\frac{1}{2}AI.BI\sin \alpha ,S_{ADI}=\frac{1}{2}AI.DI\sin \left({180}^0-\alpha \right)=\frac{1}{2}AI.DI\sin \alpha$

Suy ra $S_{ABD}=S_{ABI}+S_{ADI}=\frac{1}{2}AI\left(BI+DI\right)\sin \alpha =\frac{1}{2}AI.BD.\sin \alpha$

Tương tự ta suy ra $S_{BCD}=S_{BIC}+S_{CDI}=\frac{1}{2}CI.BD.\sin \alpha$

Từ đó suy ra $S_{ABCD}=S_{ABD}+S_{BCD}=\frac{1}{2}BD.\left(AI+CI\right)\sin \alpha =\frac{1}{2}BD.AC.sin\alpha$

---

Giải tam giác ABC, biết

a) c = 14, A = 60⁰, B = 40⁰;                                

b) b = 4,5; A = 30⁰, C = 75⁰;

c) c = 35, A = 40⁰, C = 120⁰;                              

d) a = 137,5; B = 830, C=57⁰.

Hướng dẫn giải:

Câu a:

Ta có C = 180⁰−60⁰−40⁰ = 80⁰

Áp dụng định lí sin:  

$\begin{array}{l}\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=\frac{14}{\sin {80}^0}\Rightarrow a=\frac{14}{\sin {80}^0}.\sin {60}^0\approx 12,3\\ b=\frac{14}{\sin {80}^0}.\sin {40}^0\approx 9,1\end{array}$

Câu b:

Ta có B = 180⁰−30⁰−75⁰ = 75⁰

Áp dụng định lí sin:

$\begin{array}{l}\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=\frac{4,5}{\sin {75}^0}\Rightarrow a=\frac{4,5}{\sin {75}^0}.\sin {30}^0\approx 2,3\\ c=\frac{4,5}{\sin {75}^0}.\sin {75}^0=4,5\end{array}$

Câu c:

Ta có B = 180⁰−12⁰0−40⁰ = 20⁰

Áp dụng định lí sin:

$\begin{array}{l}\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=\frac{35}{\sin {120}^0}\Rightarrow a=\frac{35}{\sin {120}^0}.\sin {40}^0\approx 26\\ b=\frac{35}{\sin {120}^0}.\sin {20}^0\approx 13,8\end{array}$

Câu d:

Ta có A = 180⁰−83⁰−57⁰ = 40⁰

Áp dụng định lí sin:

$\begin{array}{l}\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=\frac{137,5}{\sin {40}^0}\Rightarrow b=\frac{137,5}{\sin {40}^0}.\sin {83}^0\approx 212,3\\ c=\frac{137,5}{\sin {40}^0}.\sin {57}^0\approx 179,4\end{array}$

---

Giải tam giác ABC, biết

a) a = 6,3, b=6,3,C = 54⁰;                            

b) b = 32, c = 45, A = 87⁰;

c) a = 7, b = 23, C = 130⁰.

Hướng dẫn giải:

Câu a:

ABC là tam giác cân tại C ⇒ $\hat{A}=\hat{B}=\frac{{180}^0-{54}^0}{2}={63}^0$. Áp dụng định lí sin ta có:

$\frac{a}{\sin A}=\frac{c}{\mathrm{sinC}}=\frac{6,3}{\sin {63}^0}\Rightarrow c=\frac{6,3}{\sin {63}^0}.\sin {54}^0\approx 5,7$

Câu b:

Áp dụng định lí cosin ta có:

$\begin{array}{l}{a}^2=b^2+c^2-2bc.\cos A\\ ={32}^2+{45}^2-2.32.45.cos{87}^0\approx 2898,27\\ \Rightarrow a\approx 53,8\end{array}$

Áp dụng định lí sin ta có:

$\begin{array}{l}\frac{a}{\sin A}=\frac{b}{\sin B}\Rightarrow \sin B=\frac{b\sin A}{a}=\frac{32.\sin {87}^0}{53,8}\approx 0,6\\ \Rightarrow B\approx {36}^0,C\approx {57}^0\end{array}$

Câu c:

Áp dụng định lí cosin ta có:

$\begin{array}{l}{c}^2=a^2+b^2-2ab\cos C\\ =7^2+{23}^2-2.7.23cos{130}^0\approx 785\\ \Rightarrow c\approx 28\\ \cos A=\frac{b^2+c^2-a^2}{2bc}=\frac{{23}^2+{28}^2-7^2}{2.23.28}\approx 0,98\\ \Rightarrow A={11}^0,B={39}^0\end{array}$

---

Giải tam giác ABC, biết

a) a = 14, b = 18, c = 20;                                 

b) a = 6, b = 7,3, c = 4,8;

c) a = 4, b = 5, c = 7.

Hướng dẫn giải:

Câu a:

Áp dụng định lí cosin ta có:

$\begin{array}{l}\cos A=\frac{b^2+c^2-a^2}{2bc}=\frac{{18}^2+{20}^2-{14}^2}{2.18.20}\approx 0,73\\ \cos B=\frac{a^2+c^2-b^2}{2ac}=\frac{{14}^2+{20}^2-{18}^2}{2.14.20}\approx 0,49\\ \Rightarrow A\approx {43}^0,B\approx {61}^0,C\approx {76}^0\end{array}$

Câu b:

Áp dụng định lí cosin ta có:

$\begin{array}{l}\cos A=\frac{b^2+c^2-a^2}{2bc}=\frac{{\left(7,3\right)}^2+{\left(4,8\right)}^2-6^2}{2.7,3.4,8}\approx 0,58\\ \cos B=\frac{a^2+c^2-b^2}{2ac}=\frac{6^2+{\left(4,8\right)}^2-{\left(7,3\right)}^2}{2.6.\left(4,8\right)}\approx 0,1\\ \Rightarrow A\approx {55}^0,B\approx {85}^0,C\approx {40}^0\end{array}$

Câu c:

Áp dụng định lí cosin ta có:

$\begin{array}{l}\cos A=\frac{b^2+c^2-a^2}{2bc}=\frac{5^2+7^2-4^2}{2.5.7}\approx 0,83\\ \cos B=\frac{a^2+c^2-b^2}{2ac}=\frac{4^2+7^2-5^2}{2.4.7}\approx 0,71\\ \Rightarrow A\approx {34}^0,B\approx {44}^0,C\approx {102}^0\end{array}$

---

Biết hai lực cùng tác dụng vào một vật và tạo với nhau góc 40⁰. Cường độ của hai lực đó là 3N và 4N. Tính cường độ của lực tổng hợp.

Hướng dẫn giải:

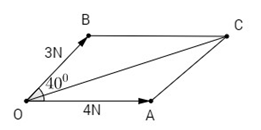
Theo quy tắc hình bình hành, ta vẽ hình bình hành AOBC thì $\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}$.

Ta có OBC = 180⁰−40⁰ = 140⁰ (Theo tính chất hình bình hành)

Áp dụng định lí cosin trong tam giác OBC. Ta có

$\begin{array}{l}O{C}^2=O{B}^2+B{C}^2-2OB.BC.\cos OBC\\ =3^2+4^2-2.3.4.\cos {140}^0\approx 43,4\\ \Rightarrow OC\approx 6,6\end{array}$

Vậy cường độ của lực tổng  hợp là 6,6N.

---

Từ vị trí A người ta quan sát một cây cao (h.61)

Biết AH = 4m, HB = 20m, BAC = 45⁰. Tính chiều cao của cây.

Hướng dẫn giải:

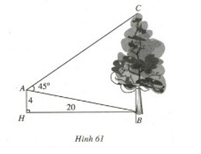
Tam giác AHB vuông tại H nên AB² = AH²+HB² = 4²+20² = 416

$\begin{array}{l}\Rightarrow AB\approx 20,4\\ \tan \widehat{BAH}=\frac{HB}{HA}=\frac{20}{4}=5\\ \Rightarrow \widehat{BAH}\approx 78,7^0\\ \Rightarrow \widehat{HAC}\approx 78,7^0+{45}^0\approx 123,7^0\\ \widehat{HAB}+\widehat{HBA}={90}^0\\ \widehat{ABC}+\widehat{HBA}={90}^0\\ \Rightarrow \widehat{HAB}=\widehat{ABC}\\ \Rightarrow \widehat{BCA}={180}^0-\widehat{BAC}-\widehat{ABC}={180}^0-\widehat{HAC}\\ \Rightarrow \widehat{BCA}\approx {180}^0-123,7^0=56,3^0\end{array}$

Ta có:

$\begin{array}{l}\frac{BC}{\sin {45}^0}=\frac{AB}{\sin 56,3^0}\\ \Rightarrow BC=\frac{20,4}{\sin 56,3^0}.sin{45}^0\approx 17,4\end{array}$

Vậy cây cao 17,4m.

---

Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ vị trí quan sát A cao 7m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50⁰ và 40⁰ so với phương nằm ngang. Tính chiều cao của tòa nhà (h.62).

Hướng dẫn giải:

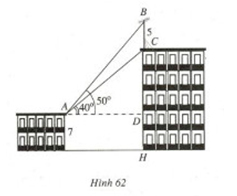
Đặt CD = x, ta có

$\begin{array}{l}\tan {40}^0=\frac{x}{AD};\tan {50}^0=\frac{BD}{AD}=\frac{x+5}{AD}\\ \Rightarrow \frac{x+5}{x}=\frac{\tan {50}^0}{\tan {40}^0}\approx 1,42\\ \Rightarrow 0,42x=5\\ \Rightarrow x=11,9\end{array}$

Vậy chiều cao tòa nhà là HC = HD+DC = 7+11,9 = 18,9m.

 

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 2 Bài 3 Hệ thức lượng trong tam giác bất kì với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.