Để giúp các em ôn tập các bài về giải toán, Chúng tôi mời các em tham khảo bài học dưới đây. Hy vọng qua bài học này sẽ giúp các em ôn tập thật tốt bài Hình tam giác
Tóm tắt lý thuyết
1.1. Kiến thức cần nhớ
a) Hình tam giác
Hình tam giác ABC có:
- Ba cạnh là: cạnh AB, cạnh AC, cạnh BC.
- Ba đỉnh là: đỉnh A, đỉnh B, đỉnh C.
- Ba góc là:
Góc đỉnh A, cạnh AB và AC (gọi tắt là góc A);
Góc đỉnh B, cạnh BA và BC (gọi tắt là góc B);
Góc đỉnh C, cạnh AC và CB (gọi tắt là góc C)
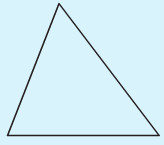
Hình tam giác có ba góc nhọn
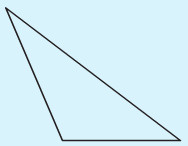
Hình tam giác có một góc tù và hai góc nhọn
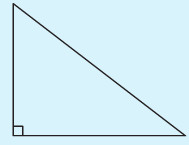
Hình tam giác có một góc vuông và hai góc nhọn (gọi là hình tam giác vuông)
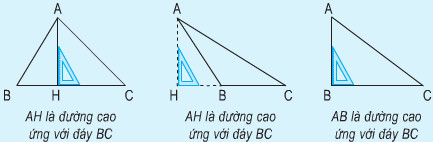
b) Đáy và đường cao
BC là đáy, AH là đường cao ứng với đáy BC. Độ dài AH là chiều cao.
1.2. Giải bài tập SGK trang 86
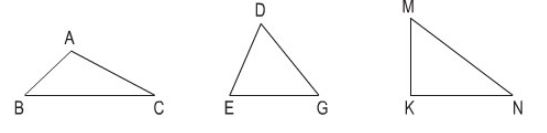
Bài 1 SGK trang 86:
Viết tên ba góc và ba cạnh của mỗi hình tam giác dưới đây:
Hướng dẫn giải:
- Hình tam giác ABC :
Ba góc là góc A, góc B, góc C
Ba cạnh là AB, AC, BC
- Hình tam giác DEG :
Ba góc là : góc D, góc E, góc G
Ba cạnh là: DE, DG, EG
- Hình tam giác KMN:
Ba góc là: góc M, góc K, góc N
Ba cạnh là MK, MN, KN.
Bài 2 SGK trang 86:
Hãy chỉ ra đáy và đường cao tương ứng được vẽ trong mỗi hình tam giác dưới đây:
Hướng dẫn giải:
- Hình tam giác ABC: đáy là AB, đường cao tương ứng là CH.
- Hình tamg giác DEG: đáy là EG, đường cao tương ứng là DK.
- Hình tam giác MPQ: đáy là PQ, đường cao tương ứng là MN.
Bài 3 SGK trang 86:
So sánh diện tích của:
a) Hình tam giác AED và hình tam giác EDH.
b) Hình tam giác EBC và hình tam giác EHC.
c) Hình chữ nhật ABCD và hình tam giác EDC.
Hướng dẫn giải:
a) Diện tích tam giác AED = Diện tích tam giác EDH.
b) Diện tích tam giác EBC = Diện tích tam giác EHC.
c) Diện tích hình chữ nhật ABCD = 2 lần diện tích tam giác EDC.
Bài tập minh họa
Bài 1: Viết tên ba góc và ba cạnh của mỗi hình tam giác dưới đây:
.png)
Giải
Hình a:
Ba góc là góc A, góc B, góc C
Ba cạnh là AB, AC, BC
Hình b:
Ba góc là: góc D, góc E, góc F
Ba cạnh là: DE, DF, EF
Hình c:
Ba góc là: góc G, góc H, góc I
Ba cạnh là GH, GI, HI.
Bài 2: Cho tam giác ABC. Trên cạnh BC lấy điểm I, sao cho IB=IC. Nối AI, trên đoạn AI lấy điểm M để có MI = ½ AM. Nối và kéo dài đoạn CM cắt cạnh AB tại N. So sánh diện tích 2 hình tam giác AMN và BMN.
Giải
Ta có
\({S_{MIC}} = \frac{1}{2}{S_{MCA}}\)
\({S_{MIC}} = {S_{MIB}}\)
Cho ta: \({S_{AMC}} = {S_{BMC}}\)
Hai tam giác AMC và BMC có chung đáy MC. Nên 2 đường cao kẻ từ A và từ B xuống cạnh đáy MC bằng nhau.
Hai đường cao này cũng chính là 2 đường cao của 2 tam giác AMN và BMN. Hai tam giác này lại có cạnh đáy chung là MN.
Vậy: \({S_{AMN}} = {S_{BMN}}\)
Lời kết
Hỏi đáp về Hình tam giác
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp. Cộng đồng Toán Chúng tôi sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
