Bài 10 trang 195 SGK Toán 11 nâng cao
a. Tính f′(3) và f′(−4) nếu f(x) = x3
b. Tính f′(1) và f′(9) nếu \(f(x) = \sqrt x \)
Hướng dẫn giải:
Câu a:
Với x0 ∈ R ta có:
\(\begin{array}{ccccc}
f\prime (x{ & _0}) = \mathop {lim}\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\\
= \mathop {lim}\limits_{x \to {x_0}} \frac{{{x^3} - x_0^3}}{{x - {x_0}}} = \mathop {lim}\limits_{x \to {x_0}} (x + x{x_0} + x_0^2) = 3x_0^2
\end{array}\)
Suy ra f′(3) = 27, f′(−4) = 48
Câu b:
Với x0 > 0, ta có:
\(\begin{array}{ccccc}
f\prime (x{ & _0}) = \mathop {lim}\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\\
= \mathop {lim}\limits_{x \to {x_0}} \frac{{\sqrt x - \sqrt {{x_0}} }}{{x - {x_0}}} = \mathop {lim}\limits_{x \to {x_0}} \frac{1}{{\sqrt x + \sqrt {{x_0}} }} = \frac{1}{{2\sqrt {{x_0}} }}\\
\Rightarrow f\prime (1) = \frac{1}{2},f\prime (9) = \frac{1}{6}
\end{array}\)
Bài 11 trang 195 SGK Toán 11 nâng cao
Cho hàm số y = f(x) có đạo hàm tại điểm x0 và đồ thị (G). Mệnh đề sau đây đúng hay sai ?
a. Nếu f′(x0) = 0 thì tiếp tuyến của (G) tại điểm M(x0; f(x0)) song song với trục hoành.
b. Nếu tiếp tuyến của G tại điểm M(x0; f(x0)) song song với trục hoành thì f′(x0) = 0
Hướng dẫn giải:
Câu a:
Mệnh đề sai vì tiếp tuyến có thể trùng với trục hoành.
Ví dụ : Cho hàm số f(x)=x2 với x0=0 thì f′(0) = 0 và tiếp tuyến tại điểm O(0 ; 0) trùng với trục hoành.
Mệnh đề sau đây mới đúng : “Nếu f′(x0) = 0 thì tồn tại tiếp tuyến tại điểm M0(x0;f(x0)) của đồ thị hàm số y = f(x) song song hoặc trùng với trục hoành”
Câu b:
Mệnh đề đúng : vì nếu tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M0(x0; f(x0)) song song với trục hoành thì hệ số góc của tiếp tuyến phải bằng 0, suy ra f′(x0) = 0
Bài 12 trang 195 SGK Toán 11 nâng cao
Hình 5.4 là đồ thị của hàm số y = f(x) trên khoảng (a ; b). Biết rằng tại các điểm M1, M2 và M3, đồ thị hàm số có tiếp tuyến được thể hiện trên hình vẽ. Dựa vào hình vẽ, em hãy nêu nhận xét về dấu của f′(x1), f′(x2) và f′(x3)
Hướng dẫn giải:
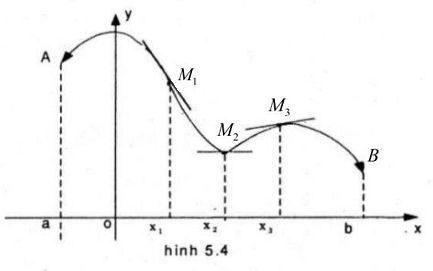
Đồ thị của hàm số y = f(x) có tiếp tuyến tại các điểm M1, M2 và M3 nên hàm số y = f(x) có đạo hàm tại các điểm x1, x2 và x3. Ta nhận thấy :
+ Tiếp tuyến tại các điểm M1 là một đường thẳng “đi xuống” từ trái sang phải, nên hệ số góc của tiếp tuyến là một số âm, suy ra f′(x1) < 0
+ Tiếp tuyến tại điểm M2 là một đường thẳng song song với trục hoành nên hệ số góc của tiếp tuyến bằng 0, suy ra f′(x2) = 0
+ Tiếp tuyến tại điểm M3 là một đường thẳng “đi lên” từ trái sang phải, nên hệ số góc của tiếp tuyến là một số dương, suy ra f′(x3) > 0
Bài 13 trang 195 SGK Toán 11 nâng cao
Chứng minh rằng để đường thẳng y = ax + b là tiếp tuyến của đồ thị hàm số y = f(x) tại điểm (x0; f(x0)), điều kiện cần và đủ là \(\left\{ \begin{array}{l}
a = f\prime ({x_0})\\
a{x_0} + b = f({x_0})
\end{array} \right.\)
Hướng dẫn giải:
Đường thẳng (d):y = ax + b là tiếp tuyến của đồ thị (G) của hàm số f tại điểm (x0; f(x0)) khi và chỉ khi đồng thời xảy ra :
(d) và (G) cùng đi qua điểm (x0; f(x0)), tức là ax0 + b = f(x0)
Hệ số góc của (d) bằng đạo hàm của f tại x0, tức là a = f′(x0)
Từ đó suy ra đpcm.
Bài 14 trang 195 SGK Toán 11 nâng cao
Cho hàm số y = |x|
a. Chứng minh rằng hàm số đã cho liên tục tại điểm x = 0
b. Tính đạo hàm của hàm số tại x = 0, nếu có.
c. Mệnh đề “Hàm số liên tục tại điểm x0 thì có đạo hàm tại x0 ” đúng hay sai ?
Hướng dẫn giải:
Câu a:
Ta có: \(\mathop {lim}\limits_{x \to 0} f(x) = \mathop {lim}\limits_{x \to 0} |x| = 0 = f(0)\)
Vậy f liên tục tại x = 0
Câu b:
Ta có:
\(\begin{array}{l}
\mathop {lim}\limits_{x \to {0^ + }} \frac{{f(x) - f(0)}}{x} = \mathop {lim}\limits_{x \to {0^ + }} \frac{{|x|}}{x} = \mathop {lim}\limits_{x \to 0} \frac{x}{x} = 1\\
\mathop {lim}\limits_{x \to {0^ - }} \frac{{f(x) - f(0)}}{x} = \mathop {lim}\limits_{x \to {0^ - }} \frac{{|x|}}{x} = \mathop {lim}\limits_{x \to 0} \frac{{ - x}}{x} = - 1
\end{array}\)
Do đó không tồn tại \(\mathop {lim}\limits_{x \to 0} \frac{{f(x) - f(0)}}{x}\) nên hàm số f không có đạo hàm tại x = 0
Câu c:
Mệnh đề sai. Thật vậy, hàm số f(x) = |x| liên tục tại điểm 0 (theo câu a) nhưng không có đạo hàm tại điểm đó (theo câu b).
Bài 15 trang 195 SGK Toán 11 nâng cao
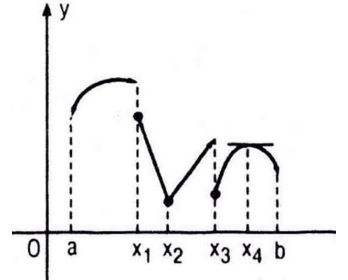
Hình 5.5 là đồ thị của hàm số y = f(x) xác định trên khoảng (a ; b). Dựa vào hình vẽ, hãy cho biết tại mỗi điểm x1, x2, x3 và x4:
a. Hàm số có liên tục hay không ?
b. Hàm số có đạo hàm hay không ? Hãy tính đạo hàm nếu có.
Hướng dẫn giải:
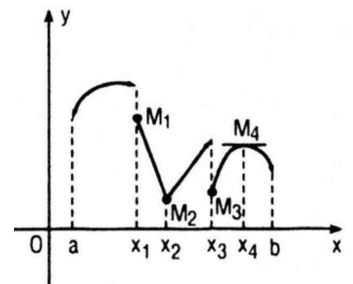
Dựa vào hình vẽ ta thấy :
+ Hàm số đã cho gián đoạn tại các điểm x1 và x3; vì đồ thị hàm số bị ngắt quãng khi đi qua các điểm M1 và M3.
+ Hàm số đã cho liên tục tại các điểm x2 và x4; vì đồ thị hàm số là đường “liền nét” khi đi qua các điểm M2 và M4
+ Hàm số không có đạo hàm tại điểm x2; vì điểm M2 đồ thị là đường “gấp khúc” (và hiển nhiên tại đó không có tiếp tuyến của đồ thị hàm số), giống như đồ thị hàm số y = |x|
+ Hàm số có đạo hàm tại điểm M4 và f′(x4) = 0; vì tại điểm M4 đồ thị của hàm số có tiếp tuyến và tiếp tuyến này song song với trục hoành.
Trên đây là nội dung hướng dẫn giải chi tiết bài tập SGK nâng cao môn Toán 11 Chương 5 Luyện tập trang 195 được trình bày rõ ràng, cụ thể với phương pháp ngắn gọn và khoa học. Hy vọng rằng đây sẽ là tài liệu hữu ích giúp các em học sinh lớp 11 học tập thật tốt!
