Giải Toán 10 SGK nâng cao Ôn tập Chương 4 Bất đẳng thức và chứng minh bất đẳng thức

Chứng minh các bất đẳng thức

a) |a+b| < |1+ab| với |a| < 1; |b| < 1

b) \(\frac{1}{{n + 1}} + \frac{1}{{n + 2}} + ... + \frac{1}{{2n}} \ge \frac{1}{2}\) với mọi n ∈ N*

c) \(\frac{{a + b}}{{1 + a + b}} \le \frac{a}{{1 + a}} + \frac{b}{{1 + b}}\) với mọi a ≥ 0; b ≥ 0. Khi nào có đẳng thức?

Hướng dẫn giải:

Câu a:

Ta có:

 |a+b| < |1+ab| ⇔ (a+b)² < (1+ab)²

⇔ a²b²–a²–b²+1 > 0 ⇔ a²(b²–1)–(b²–1) > 0

⇔ (a²–1)(b²–1) > 0 (luôn đúng vì a² < 1 và b² < 1)

Vậy với |a| < 1; |b| < 1 thì |a+b| < |1+ab|

Câu b:

Ta có:

\(\frac{1}{{n + 1}} \ge \frac{1}{{2n}};\frac{1}{{n + 2}} \ge \frac{1}{{2n}};...;\frac{1}{{2n}} = \frac{1}{{2n}}\)

Do đó:

\(\begin{array}{l}
\frac{1}{{n + 1}} + \frac{1}{{n + 2}} + ... + \frac{1}{{2n}} \ge \underbrace {\frac{1}{{2n}} + \frac{1}{{2n}} + ... + \frac{1}{{2n}}}_n\\
 \Rightarrow \frac{1}{{n + 1}} + \frac{1}{{n + 2}} + ... + \frac{1}{{2n}} \ge n.\frac{1}{{2n}} = \frac{1}{2}
\end{array}\)

Vậy ta được điều phải chứng minh.

Câu c:

Vì a ≥ 0; b ≥ 0 nên:

\(\frac{{a + b}}{{1 + a + b}} = \frac{a}{{1 + a + b}} + \frac{b}{{1 + a + b}} \le \frac{a}{{1 + a}} + \frac{b}{{1 + b}}\)

Dấu “=” xảy ra khi và chỉ khi a = b = 0

---

Chứng minh các bất đẳng thức sau:

a) \(a + b + c \ge \sqrt {ab}  + \sqrt {bc}  + \sqrt {ca} \) với \(a \ge 0,b \ge 0,c \ge 0\)        

b) a²b² + b²c² + c²a² ≥ abc(a + b +c) với mọi a,b,c ∈ R

Khi nào có đẳng thức?

Hướng dẫn giải:

Câu a:

Ta có:

\(\begin{array}{l}
a + b + c \ge \sqrt {ab}  + \sqrt {bc}  + \sqrt {ca} \\
 \Leftrightarrow 2a + 2b + 2c - 2\sqrt {ab}  - 2\sqrt {bc}  - 2\sqrt {ca}  \ge 0\\
 \Leftrightarrow \left( {a - 2\sqrt {ab}  + b} \right) + \left( {b - 2\sqrt {bc}  + c} \right) + \left( {c - 2\sqrt {ca}  + a} \right) \ge 0\\
 \Leftrightarrow {\left( {\sqrt a  - \sqrt b } \right)^2} + {\left( {\sqrt b  - \sqrt c } \right)^2} + {\left( {\sqrt c  - \sqrt a } \right)^2} \ge 0
\end{array}\)

Dấu “=” xảy ra khi và chỉ khi a = b = c

Câu b:

Ta có:

a²b² + b²c² + c²a² ≥ abc(a + b +c)

⇔ 2a²b² + 2b²c² + 2c²a² ≥ 2abc(a + b +c)

⇔ (a²b² – 2a²bc+ a²c²) + (a²c² – 2c²ab +b²c²) +(a²b² – 2b²ac +b²c²) ≥ 0

⇔  (ab – ac)² + (ac – bc)² + (ab – bc)² ≥ 0 (luôn đúng)

Dấu “=” xảy ra khi và chỉ khi a = b = c hoặc 2 trong 3 số a, b, c = 0

---

Tìm giá trị nhỏ nhất của các hàm số sau

a) \(f\left( x \right) = \left| {x + \frac{1}{x}} \right|\)

b) \(g\left( x \right) = \frac{{{x^2} + 2}}{{\sqrt {{x^2} + 1} }}\)

Hướng dẫn giải:

Câu a:

Vì với mọi x ≠ 0; x và \(\frac{1}{x}\) cùng dấu nên:

\(f\left( x \right) = \left| {x + \frac{1}{x}} \right| = \left| x \right| + \frac{1}{{\left| x \right|}} \ge 2\sqrt {\left| x \right|.\frac{1}{{\left| x \right|}}}  = 2\) với mọi x ≠ 0

Dấu “=” xảy ra khi và chỉ khi \(\left| x \right| = \frac{1}{{\left| x \right|}} \Leftrightarrow \left| x \right| = 1 \Leftrightarrow x =  \pm 1\)

Vậy giá trị nhỏ nhất của f(x) là 2.

Câu b:

Với mọi x ∈ R, ta có:

\(g\left( x \right) = \frac{{{x^2} + 2}}{{\sqrt {{x^2} + 1} }} = \frac{{{x^2} + 1}}{{\sqrt {{x^2} + 1} }} + \frac{1}{{\sqrt {{x^2} + 1} }} = \sqrt {{x^2} + 1}  + \frac{1}{{\sqrt {{x^2} + 1} }} \ge 2\sqrt {\sqrt {{x^2} + 1} .\frac{1}{{\sqrt {{x^2} + 1} }}}  = 2\) (theo bất đẳng thức Cô-si)

\(g\left( x \right) = 2 \Leftrightarrow \sqrt {{x^2} + 1}  = \frac{1}{{\sqrt {{x^2} + 1} }} \Leftrightarrow {x^2} + 1 = 1 \Leftrightarrow x = 0\)

Vậy giá trị nhỏ nhất của g(x) là 2.

---

Tìm các giá trị của tham số m sao cho hệ bất phương trình sau có nghiệm.

\(\left\{ \begin{array}{l}
\frac{7}{6}x - \frac{1}{2} > \frac{{3x}}{2} - \frac{{13}}{3}\\
{m^2}x + 1 \ge {m^4} - x
\end{array} \right.\)

Hướng dẫn giải:

Ta có:

\(\frac{7}{6}x - \frac{1}{2} > \frac{{3x}}{2} - \frac{{13}}{3} \Leftrightarrow 7x - 3 > 9x - 26 \Leftrightarrow x < \frac{{23}}{2}\)

Bất phương trình thứ hai của hệ tương đương với:

(m² + 1)x ≥ m⁴ – 1 hay x ≥ m² – 1

Hệ đã cho có nghiệm khi và chỉ khi:

\({m^2} - 1 < \frac{{23}}{2} \Leftrightarrow {m^2} < \frac{{25}}{2} \Leftrightarrow \left| m \right| < \frac{{5\sqrt 2 }}{2} \Leftrightarrow  - \frac{{5\sqrt 2 }}{2} < m < \frac{{5\sqrt 2 }}{2}\)

---

Với giá trị nào của m, bất phương trình:

(m² + 1)x + m(x + 3) + 1 > 0 nghiệm đúng ∀x ∈ [-1; 2] ?

Hướng dẫn giải:

Ta viết phương trình đã cho dưới dạng:

(m² + m + 1)x + 3m + 1 > 0

Đặt f(x) = (m² + m + 1)x + 3m + 1 ,

Với mỗi giá trị của m, đồ thị của hàm số y = f(x) là đường thẳng (Dm).

Gọi A_m và B_m là các điểm trên đường thẳng (D_m) có hoành độ theo thứ tự là – 1 và 2.

 

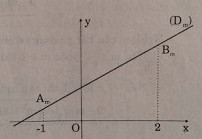
f(x) > 0 với ∀x ∈ [-1; 2] khi và chỉ khi đoạn thẳng A_mB_m nằm phía trên trục hoành. Điều này xảy ra khi và chỉ khi A_m và B_m nằm phía trên trục hoành, tức là: 

\(\left\{ \begin{array}{l}
f\left( { - 1} \right) > 0\\
f\left( 2 \right) > 0
\end{array} \right.\)

Thay f(-1) = - m² + 2m và f(2) = 2m²+ 5m + 3, ta được hệ bất phương trình:

\(\left\{ \begin{array}{l}
 - {m^2} + 2m > 0\\
2{m^2} + 5m + 3 > 0
\end{array} \right. \Leftrightarrow 0 < m < 2\)

---

Giải và biện luận các bất phương trình sau:

a) a²x + 1 > (3a - 2)x - 3

b) 2x² + (m - 9)x + m² + 3m + 4 ≥ 0

Hướng dẫn giải:

Câu a:

Bất phương trình đã cho tương đương với bất phương trình:

(a² – 3a + 2) x > 2

• Nếu a2 – 3a + 2 > 0, tức là a < 1 hay a > 2 thì nghiệm của bất phương trình đã cho là \(x > \frac{2}{{{a^2} - 3a + 2}}\)
• Nếu a² – 3a + 2 < 0,  tức là 1 < a <  2 thì nghiệm của bất phương trình đã cho là \(x < \frac{2}{{{a^2} - 3a + 2}}\)
• Nếu a² – 3a + 2 = 0, tức là a = 1 hoặc a = 2 thì bất phương trình đã cho trở thành 0x > 2. Khi đó, bất phương trình này vô nghiệm.

Câu b:

Ta có:

Δ = (m – 9)² – 8(m² + 3m + 4) = - 7(m² + 6m – 7)

• Nếu Δ ≤ 0 hay m ≤ -7 hoặc m ≥ 1 thì bất phương trình đã cho nghiệm đúng với mọi x ∈ R
• Nếu Δ  > 0 hay -7 < m < 1 thì tam thức ở vế trái của bất phương trình có hai nghiệm phân biệt : 

\(\begin{array}{l}
{x_1} = \frac{{9 - m - \sqrt { - 7\left( {{m^2} + 6m - 7} \right)} }}{4}\\
{x_2} = \frac{{9 - m + \sqrt { - 7\left( {{m^2} + 6m - 7} \right)} }}{4}
\end{array}\)

Suy ra tập nghiệm của bất phương trình đã cho là: x ≤ x1 hoặc x ≥ x2.

 Vậy:

• Nếu m ≤ - 7 hoặc m ≥ 1 thì tập nghiệm của bất phương trình đã cho là R
• Nếu - 7 < m < 1 thì tập nghiệm của bất phương trình đã cho là:

\(\left( { - \infty ;\frac{{9 - m - \sqrt { - 7\left( {{m^2} + 6m - 7} \right)} }}{4}} \right) \cup \left( {\frac{{9 - m + \sqrt { - 7\left( {{m^2} + 6m - 7} \right)} }}{4}; + \infty } \right)\)

---

Giải các bất phương trình sau:

a) \(\frac{{x - 2}}{{{x^2} - 9x + 20}} > 0\)

b) \(\frac{{2{x^2} - 10x + 14}}{{{x^2} - 3x + 2}} \ge 1\)

Hướng dẫn giải:

Câu a:

Bảng xét dấu

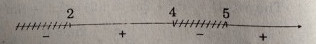
Vậy \(S = \left( {2;4} \right) \cup \left( {5; + \infty } \right)\)

Câu b:

Bất phương trình đã cho tương đương với bất phương trình:

\(\begin{array}{l}
\frac{{2{x^2} - 10x + 14}}{{{x^2} - 3x + 2}} - 1 \ge 0\,\,\,\\
 \Leftrightarrow \frac{{2{x^2} - 7x + 12}}{{{x^2} - 3x + 2}} \ge 0
\end{array}\)

Bảng xét dấu

Tập nghiệm của bất phương trình là \(S = \left( { - \infty ;1} \right) \cup \left( {2;3} \right] \cup \left( {4; + \infty } \right)\)

---

Tìm các giá trị của m sao cho R là tập nghiệm của mỗi bất phương trình:

a) (m - 4)x² - (m - 6)x + m – 5 ≤ 0

b) (m² - 1)x² + 2(m + 1)x + 3 > 0

Hướng dẫn giải:

Câu a:

• Với m = 4, bất phương trình thành 2x – 1 ≤  0, không thỏa mãn điều kiện với mọi x
• Với m ≠ 4: (m - 4)x² - (m - 6)x + m – 5 ≤ 0, ∀x

\(\begin{array}{l}
 \Leftrightarrow \left\{ \begin{array}{l}
m - 4 < 0\\
\Delta  = {\left( {m - 6} \right)^2} - 4\left( {m - 4} \right)\left( {m - 5} \right) \le 0
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
m < 4\\
 - 3{m^2} + 24m - 44 \le 0
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
m < 4\\
\left[ \begin{array}{l}
m \le 4 - \frac{{2\sqrt 3 }}{2}\\
m \ge 4 + \frac{{2\sqrt 3 }}{2}
\end{array} \right.
\end{array} \right. \Leftrightarrow m \le 4 - \frac{{2\sqrt 3 }}{2}
\end{array}\)

Câu b:

• Với m = 1, bất phương trình trở thành 4x + 3 > 0 , không thỏa mãn với mọi x
• Với m = -1, bất phương trình trở thành 3 > 0 thỏa mãn với mọi x
• Với m ≠ - 1, (m² - 1)x² + 2(m + 1) + 3 > 0, ∀x

\(\begin{array}{l}
 \Leftrightarrow \left\{ \begin{array}{l}
{m^2} - 1 > 0\\
\Delta ' = {\left( {m + 1} \right)^2} - 3\left( {{m^2} - 1} \right) < 0
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
\left[ \begin{array}{l}
m <  - 1\\
m > 1
\end{array} \right.\\
 - 2{m^2} + 2m + 4 < 0
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
\left[ \begin{array}{l}
m <  - 1\\
m > 1
\end{array} \right.\\
\left[ \begin{array}{l}
m <  - 1\\
m > 2
\end{array} \right.
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
m <  - 1\\
m > 2
\end{array} \right.
\end{array}\)

Vậy với m ≤ -1 hoặc m > 2 thì bất phương trình đã cho có tập nghiệm là R

---

Giải các phương trình sau

a) |x²–2x–3| = 2x+2

b) \(\sqrt {{x^2} - 4}  = 2\left( {x - \sqrt 3 } \right)\)

Hướng dẫn giải:

Câu a:

Điều kiện: x ≥−1. Ta có:

\(\begin{array}{l}
\left| {{x^2} - 2x - 3} \right| = 2x + 2\\
 \Leftrightarrow \left[ \begin{array}{l}
{x^2} - 2x - 3 = 2x + 2\\
{x^2} - 2x - 3 =  - 2x - 2
\end{array} \right.\\
 \Leftrightarrow \left[ \begin{array}{l}
{x^2} - 4x - 5 = 0\\
{x^2} - 1 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x =  - 1,x = 5\\
x =  \pm 
\end{array} \right.\left( n \right)
\end{array}\)

Vậy S = {-1, 1, 5}

Câu b:

Ta có:

\(\begin{array}{l}
\sqrt {{x^2} - 4}  = 2\left( {x - \sqrt 3 } \right) \Leftrightarrow \left\{ \begin{array}{l}
x \ge \sqrt 3 \\
3{x^2} - 8\sqrt 3 x + 16 = 0
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
x \ge \sqrt 3 \\
x = \frac{{4\sqrt 3 }}{3}
\end{array} \right.
\end{array}\)

Vậy \(S = \left\{ {\frac{{4\sqrt 3 }}{3}} \right\}\)

---

Giải các bất phương trình sau:

a) \(\sqrt {{x^2} - 4x - 12}  \le  - 4\)

b) \(\left( {x - 2} \right)\sqrt {{x^2} + 4}  \le {x^2} - 4\)

c) \(\sqrt {{x^2} - 8x}  \ge 2\left( {x + 1} \right)\)

d) \(\sqrt {x\left( {x + 3} \right)}  \le 6 - {x^2} - 3x\)

Hướng dẫn giải:

Câu a:

Ta có:

\(\begin{array}{l}
\sqrt {{x^2} - 4x - 12}  \le  - 4\\
 \Leftrightarrow \left\{ \begin{array}{l}
{x^2} - 4x - 12 \ge 0\\
x - 4 \le 0\\
{x^2} - 4x - 12 \le {\left( {x - 4} \right)^2}
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
\left[ \begin{array}{l}
x \le  - 2\\
x \ge 6
\end{array} \right.\\
x \ge 4\\
4x \le 28
\end{array} \right. \Leftrightarrow 6 \le x \le 7
\end{array}\)

Vậy S = [6,7]

Câu b:

Ta có:

\(\begin{array}{l}
\left( {x - 2} \right)\sqrt {{x^2} + 4}  \le {x^2} - 4\\
 \Leftrightarrow \left( {x - 2} \right)\left( {\sqrt {{x^2} + 4}  - x - 2} \right) \le 0
\end{array}\)

•  Với x = 2 là nghiệm của bất phương trình
• Với x > 2, ta có:

\(\left( {x - 2} \right)\sqrt {{x^2} + 4}  \le {x^2} - 4 \Leftrightarrow {x^2} + 4 \le {\left( {x + 2} \right)^2} \Leftrightarrow x \ge 0\)

Kết hợp với điều kiện, ta có: x > 2.

• Với x < 2, ta có:

\(\begin{array}{l}
\left( {x - 2} \right)\sqrt {{x^2} + 4}  \le {x^2} - 4\\
 \Leftrightarrow \left[ \begin{array}{l}
x + 2 > 0\\
\left\{ \begin{array}{l}
x + 2 \ge 0\\
{x^2} + 4 \ge {\left( {x + 2} \right)^2}
\end{array} \right.
\end{array} \right.\\
 \Leftrightarrow \left[ \begin{array}{l}
x <  - 2\\
\left\{ \begin{array}{l}
x \ge  - 2\\
x \le 0
\end{array} \right.
\end{array} \right. \Leftrightarrow x \le 0
\end{array}\)

Vậy \(S = \left( { - \infty ;0} \right] \cup \left[ {2; + \infty } \right)\)

Câu c:

Bất phương trình đã cho tương đương với:

\(\left( I \right) \Leftrightarrow \left\{ \begin{array}{l}
{x^2} - 8x \ge 0\\
x + 1 < 0
\end{array} \right. \vee \left( {II} \right) \Leftrightarrow \left\{ \begin{array}{l}
x + 1 \ge 0\\
{x^2} - 8x \ge 4{\left( {x + 1} \right)^2}
\end{array} \right.\)

Ta có:

\(\begin{array}{l}
\left( I \right) \Leftrightarrow \left\{ \begin{array}{l}
\left[ \begin{array}{l}
x \le 0\\
x \ge 8
\end{array} \right.\\
x <  - 1
\end{array} \right. \Leftrightarrow x <  - 1\\
\left( {II} \right) \Leftrightarrow \left\{ \begin{array}{l}
x \ge  - 1\\
3{x^2} + 16x + 4 \le 0
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
x \ge  - 1\\
\frac{{ - 8 - 2\sqrt {13} }}{3} \le x \le \frac{{ - 8 + 2\sqrt {13} }}{3}
\end{array} \right.\\
 \Leftrightarrow  - 1 \le x \le \frac{{ - 8 + 2\sqrt {13} }}{3}
\end{array}\)

Tập nghiệm của bất phương trình đã cho là:

\(S = \left( { - \infty ; - 1} \right) \cup \left[ { - 1;\frac{{ - 8 + 2\sqrt {13} }}{3}} \right] = \left( { - \infty ;\frac{{ - 8 + 2\sqrt {13} }}{3}} \right]\)

d) Đặt \(t = \sqrt {x\left( {x + 3} \right)} \,\,\left( {t \ge 0} \right)\)

⇒ x² + 3x = t² ⇔ t² + t - 6 ≤ 0 ⇔  - 3 ≤ t ≤ 2

Kết hợp với điều kiện: 0 ≤ t ≤ 2  ⇔  0 ≤ x² + 3x ≤ 4

\(\begin{array}{l}
 \Leftrightarrow \left\{ \begin{array}{l}
{x^2} + 3x \ge 0\\
{x^2} + 3x - 4 \le 0
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
\left[ \begin{array}{l}
x \le  - 3\\
x \ge 0
\end{array} \right.\\
 - 4 \le x \le 1
\end{array} \right.\\
 \Leftrightarrow \left[ \begin{array}{l}
 - 4 \le x \le  - 3\\
0 \le x \le 1
\end{array} \right.
\end{array}\)

Vậy S = [−4,−3]∪[0,1]

---

Với giá trị nào của a, các hệ phương trình sau có nghiệm

a) \(\left\{ \begin{array}{l}
{x^2} - 5x + 6 < 0\\
ax + 4 < 0
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
4x + 1 < 7x - 2\\
{x^2} - 2ax + 1 \le 0
\end{array} \right.\)

Hướng dẫn giải:

Câu a:

Bất phương trình đầu của hệ có nghiệm là 2 < x < 3

Bất phương trình thứ hai của hệ tương đương với bất phương trình ax < - 4

• Nếu a = 0 thì bất phương trình này vô nghiệm. Do đó, hệ vô nghiệm.
• Nếu a > 0 thì nghiệm của phương trình là \(x <  - \frac{4}{a}\)

Vì \( - \frac{4}{a} < 0\) nên hệ vô nghiệm.

• Nếu a < 0 thì nghiệm của bất phương trình này là \(x >  - \frac{4}{a}\)

Hệ có nghiệm khi và chỉ khi: 

\(\left\{ \begin{array}{l}
a < 0\\
 - \frac{4}{3} < 3
\end{array} \right. \Leftrightarrow a <  - \frac{4}{3}\)

Vậy hệ có nghiệm khi và chỉ khi \(a <  - \frac{4}{3}\)

Câu b:

Bất phương trình đầu của hệ có nghiệm là x > 1

Xét bất phương trình thứ hai của hệ:

Ta có Δ’= a² – 1

Nếu Δ’ = 0 ⇔ a = ± 1

• Với a = 1, nghiệm của bất phương trình là x = 1

Do đó, hệ vô nghiệm.

• Với a = - 1, nghiệm của bất phương trình là x = -1

Nếu Δ’ < 0 hay -1 < a < 1 thì bất phương trình này vô nghiêm.

Do đó, hệ vô nghiệm.

Nếu Δ’ > 0 hay a < -1 hoặc a > 1 thì tam thức ở vế trái của bất phương trình có hai nghiệm phân biệt x₁, x₂.

Nghiệm của bất phương trình này là x₁ ≤ 1  ≤ x₂  (giả sử x₁ < x₂)

Theo định lý Vi-ét, ta có x₁x₂ = 1 và x₁ + x₂ = 2a

• Nếu a < - 1 thì cả hai nghiệm x₁ và  x₂ đều âm. Do đó, hệ đã cho vô nghiệm.
• Nếu a > 1 thì hai nghiệm x₁ và x₂ đều dương. Ngoài ra vì x₁x₂ = 1 và x₁ ≠ x₂ nên x₁ < 1 < x₂.

Do đó, hệ có nghiệm.

---

Trong mỗi câu sau đây, có bốn khẳng định (A), (B), (C) và (D) , trong đó chỉ có một khẳng định đúng. Hãy chọn khẳng định đúng trong mỗi câu đó.

a) Tam thức bậc hai \(f\left( x \right) = {x^2} + \left( {1 - \sqrt 3 } \right)x - 8 - 5\sqrt 3 \)

A. Dương với mọi x ∈ R

B. Âm với mọi x ∈ R

C. Âm với mọi \(x \in \left( { - 2 - \sqrt 3 ;1 + 2\sqrt 3 } \right)\)       

D. Âm với mọi \(x \in \left( { - \infty ;1} \right)\)

b) Tam thức bậc hai \(f\left( x \right) = \left( {1 - \sqrt 2 } \right){x^2} + \left( {5 - 4\sqrt 2 } \right)x - 3\sqrt 2  + 6\)

A. Dương với mọi x ∈ R

B. Dương với mọi \(x \in \left( { - 3;\sqrt 2 } \right)\)

C. Dương với mọi \(x \in \left( { - 4;\sqrt 2 } \right)\)     

D. Âm với mọi x ∈ R

c) Tập xác định của hàm số \(f\left( x \right) = \sqrt {\left( {2 - \sqrt 5 } \right){x^2} + \left( {15 - 7\sqrt 5 } \right)x + 25 - 10\sqrt 5 } \)

(A). R

(B). \(\left( { - \infty ;1} \right)\)

(C). [−5;1]

(D). \(\left[ { - 5;\sqrt 5 } \right]\)

Hướng dẫn giải:

Câu a:

Vì ac < 0 nên f(x) có hai nghiệm phân biệt x₁ < x₂

Bảng xét dấu:

 

Chọn (C)

Câu b:

Vì ac < 0 nên f(x) có hai nghiệm phân biệt x₁ < x₂

Bảng xét dấu:

 

Loại trừ A, D

Ta có:

\(f\left( { - 3} \right) = 9\left( {1 - \sqrt 2 } \right) - 3\left( {5 - 4\sqrt 2 } \right) - 3\sqrt 2  + 6 = 0\)

⇒ x = −3 là nghiệm của f(x)

Chọn (B)

Câu c:

f(x) xác định \( \Leftrightarrow g\left( x \right) = \left( {2 - \sqrt 5 } \right){x^2} + \left( {15 - 7\sqrt 5 } \right)x + 25 - 10\sqrt 5  \ge 0\)

Ta có ac < 0 nên g(x) có hai nghiệm phân biệt x₁ < x₂

Bảng xét dấu:

 

Loại (A), (B)

Ta có:

\(g\left( {\sqrt 5 } \right) = 5\left( {2 - \sqrt 5 } \right) + \sqrt 5 \left( {15 - 7\sqrt 5 } \right) + \left( {25 - 10\sqrt 5 } \right) = 0\)

 \( \Rightarrow \sqrt 5 \) là nghiệm của g(x)

Do đó chọn (D)

---

a) Tập nghiệm của bất phương trình: \(\left( {3 - 2\sqrt 2 } \right){x^2} - 2\left( {3\sqrt 2  - 4} \right)x + 6\left( {2\sqrt 2  - 3} \right) \le 0\) là: 

(A). \(\left[ { - 2;3\sqrt 2 } \right]\)

(B). \(\left( { - \infty ; - 1} \right)\)

(C). \(\left[ { - 1; + \infty } \right)\)

(D). \(\left[ { - 1;3\sqrt 2 } \right]\)

b) Tập nghiệm của bất phương trình: \(\left( {2 + \sqrt 7 } \right){x^2} + 3x - 14 - 4\sqrt 7  \ge 0\) là: 

(A). R

(B). \(\left( { - \infty ; - \sqrt 7 } \right] \cup \left[ {2; + \infty } \right)\)

(C). \(\left[ { - 2\sqrt 2 ;5} \right]\)

(D). \(\left( { - \infty ; - \sqrt 7 } \right] \cup \left[ {1; + \infty } \right)\)

c) Tập nghiệm của bất phương trình: \(\frac{{\left( {x - 1} \right)\left( {{x^3} - 1} \right)}}{{{x^2} + \left( {1 + 2\sqrt 2 } \right)x + 2 + \sqrt 2 }} \le 0\)

(A). \(\left( { - 1 - \sqrt 2 ; - \sqrt 2 } \right)\)

(B). \(\left( { - 1 - \sqrt 2 ;1} \right]\)

(C). \(\left( { - 1 - \sqrt 2 ; - \sqrt 2 } \right) \cup \left\{ 1 \right\}\)

(D). \(\left[ {1; + \infty } \right)\)

Hướng dẫn giải:

Câu a:

Gọi \(f\left( x \right) = \left( {3 - 2\sqrt 2 } \right){x^2} - 2\left( {3\sqrt 2  - 4} \right)x + 6\left( {2\sqrt 2  - 3} \right)\)

Vì ac < 0 nên f(x) có hai nghiệm phân biệt x₁ < x₂

Bảng xét dấu:

 

Loại trừ (B), (C)

Ta có \(f\left( { - 2} \right) = 2\left( {3 - 2\sqrt 2 } \right) + 2\sqrt 2 \left( {3\sqrt 2  - 4} \right) + 6\left( {2\sqrt 2  - 3} \right) = 0\)

Vậy chọn A.

Câu b:

Gọi \(f\left( x \right) = \left( {2 + \sqrt 7 } \right){x^2} + 3x - 14 - 4\sqrt 7 \)

Vì ac < 0 nên f(x) có hai nghiệm phân biệt x₁ < x₂

Bảng xét dấu:

Loại trừ (A), (C)

Ta có: \(f\left( 2 \right) = 4\left( {2 + \sqrt 7 } \right) + 6 - 14 - 4\sqrt 7  = 0\)

Chọn (B)

Câu c:

Gọi \(f\left( x \right) = \frac{{\left( {x - 1} \right)\left( {{x^3} - 1} \right)}}{{{x^2} + \left( {1 + 2\sqrt 2 } \right)x + 2 + \sqrt 2 }}\)

Ta có:

f(1) = 0 nên loại trừ (A)

\(f\left( 0 \right) = \frac{1}{{2 + \sqrt 2 }} > 0\) nên loại trừ (B)

f(2) > 0 nên loại trừ D

Vậy chọn C.

---

a) Nghiệm của phương trình \(\sqrt {{x^2} + 10x - 5}  = 2\left( {x - 1} \right)\) là: 

(A). \(x = \frac{3}{4}\)

(B). \(x = 3 - \sqrt 6 \)

(C). \(x = 3 + \sqrt 6 \)

(D). \(\left\{ \begin{array}{l}
{x_1} = 3 + \sqrt 6 \\
{x_2} = 2
\end{array} \right.\)

b) Tập nghiệm của bất phương trình \(\sqrt {\left( {x + 4} \right)\left( {6 - x} \right)}  \le 2\left( {x + 1} \right)\) là:

(A). \(\left[ { - 2;5} \right]\)

(B). \(\left[ {\frac{{\sqrt {109}  - 3}}{5};6} \right]\)

(C). [1,6]

(D). [0,7]

c) Tập nghiệm của bất phương trình \(\sqrt {2\left( {x - 2} \right)\left( {x - 5} \right)}  > x - 3\) là:

(A). [−100,2]

(B). \(\left( { - \infty ;1} \right]\)

(C). \(\left( { - \infty ;2} \right) \cup \left[ {6; + \infty } \right)\)

(D). \(\left( { - \infty ;2} \right] \cup \left( {4 + \sqrt 5 ; + \infty } \right)\)

Hướng dẫn giải:

Câu a:

Điều kiện: x ≥ 1 loại trừ (A) và (B)

Thay x = 2 vào không thấy thỏa mãn phương trình, ta loại trừ (D)

Vậy chọn C

Câu b:

x = 0 không là nghiệm bất phương trình: loại trừ (A), (D)

x = 1 không là nghiệm bất phương trình, loại trừ (C)

Chọn (B)

Câu c:

x = 2 là nghiệm của bất phương trình nên trừ (B)

x = 6 là nghiệm của bất phương trình nên loại trừ (C)

x = 7 là nghiệm nên chọn D.

 

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Ôn tập Chương 4 Bất đẳng thức và chứng minh bất đẳng thức với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.