Bài 36 trang 108 SGK Hình học 10 nâng cao
Cho hypebol (H) có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\). Hỏi trong các mệnh đề sau, mệnh đề nào đúng?
a) Tiêu cự của (H) là 2c, trong đó c2 = a2+b2.
b) (H) có độ dài trục thực bằng 2a, độ dài trục ảo bằng 2b.
c) Phương trình hai đường tiệm cận của (H) là \(y = \pm \frac{a}{b}x\)
d) Tâm sai của (H) là \(e = \frac{c}{a} > 1\)
Hướng dẫn giải:
Các mệnh đề đúng là: a); b); d).
Mệnh đề sai là: c).
Bài 37 trang 109 SGK Hình học 10 nâng cao
Tìm tọa độ các tiêu điểm, các đỉnh; độ dài trục thực, trục ảo và phương trình các đường tiệm cận của mỗi hypebol có phương trình sau:
a) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{4} = 1\);
b) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\);
c) \({x^2} - 9{y^2} = 9\)
Hướng dẫn giải:
Câu a:
Ta có: \(a = 3;b = 2;c = \sqrt {{a^2} + {b^2}} = \sqrt {13} \)
Tiêu điểm \({F_1}\left( { - \sqrt {13} ;0} \right),{F_2}\left( {\sqrt {13} ;0} \right)\)
Các đỉnh A1(−3;0), A2(3;0)
Độ dài trục thực: 2a = 6 , độ dài trục ảo: 2b = 4
Phương trình tiệm cận của hypebol: \(y = \pm \frac{2}{3}x\)
Câu b:
Ta có: \(a = 3;b = 4;c = \sqrt {{a^2} + {b^2}} = 5\)
Tiêu điểm F1(−5;0), F2(5;0)
Các đỉnh A1(−3;0), A2(3;0)
Độ dài trục thực: 2a = 6, độ dài trục ảo: 2b = 8
Phương trình các đường tiệm cận của hypebol: \(y = \pm \frac{4}{3}x\)
Câu c:
Ta có: \({x^2} - 9{y^2} = 9 \Leftrightarrow \frac{{{x^2}}}{9} - {y^2} = 1\)
\(a = 3;b = 1;c = \sqrt {10} \)
Tiêu điểm \({F_1}\left( { - \sqrt {10} ;0} \right),{F_2}\left( {\sqrt {10} ;0} \right)\)
Các đỉnh: A1(−3;0), A2(3;0)
Độ dài trục thực: 2a = 6, độ dài trục ảo 2b = 2
Phương trình các đường tiệm cận của hypebol: \(y = \pm \frac{1}{3}x\)
Bài 38 trang 109 SGK Hình học 10 nâng cao
Cho đường tròn (C) tâm F1, bán kính R và một điểm F2 ở ngoài (C). Chứng minh rằng tập hợp tâm các đường tròn đi qua F2, tiếp xúc với (C) là một đường hypebol. Viết phương trình chính tắc của hypebol đó.
Hướng dẫn giải:
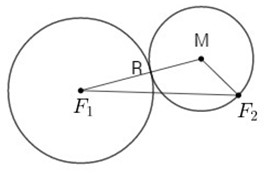
Gọi M là tâm đường tròn đi qua F2 và tiếp xúc với (C)
Ta có: |MF1−MF2| = R = 2a
Vậy tập hợp các điểm M là đường hypebol (H) có \(a = \frac{R}{2},c = \frac{{{F_1}{F_2}}}{2}\)
\( \Rightarrow {b^2} = {c^2} - {a^2} = \frac{{{F_1}{F_2}^2 - {R^2}}}{4}\)
Phương trình chính tắc của (H) là:
\(\frac{{{x^2}}}{{{{\left( {\frac{R}{2}} \right)}^2}}} - \frac{{{y^2}}}{{{{\left( {\frac{{\sqrt {{F_1}{F_2}^2 - {R^2}} }}{2}} \right)}^2}}} = 1\).
Bài 39 trang 109 SGK Hình học 10 nâng cao
Viết phương trình chính tắc của hypebol (H) trong mỗi trường hợp sau
a) (H) có một tiêu điểm là (5;0) và độ dài trục thực bằng 8;
b) (H) có tiêu cự bằng \(2\sqrt 3 \), một đường tiệm cận là \(y = \frac{2}{3}x\);
c) (H) có tâm sai \(e = \sqrt 5 \) và đi qua điểm \(\left( {\sqrt {10} ;6} \right)\).
Hướng dẫn giải:
Câu a:
Ta có: \(c = 5,a = 4 \Rightarrow {b^2} = {c^2} - {a^2} = 9\)
Vậy (H): \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\).
Câu b:
Ta có: \(c = \sqrt 3 ;\frac{b}{a} = \frac{2}{3} \Rightarrow b = \frac{{2a}}{3}\)
\(\begin{array}{l}
{c^2} = {a^2} + {b^2} = 3 \Rightarrow {a^2} + \frac{{4{a^2}}}{9} = 3\\
\Rightarrow {a^2} = \frac{{27}}{{13}},{b^2} = 3 - \frac{{27}}{{13}} = \frac{{12}}{{13}}
\end{array}\)
Vậy (H): \(\frac{{{x^2}}}{{\frac{{27}}{{13}}}} - \frac{{{y^2}}}{{\frac{{12}}{{13}}}} = 1\)
Câu c:
Ta có: \(e = \frac{c}{a} = \sqrt 5 \Rightarrow {c^2} = 5{a^2} \Rightarrow {b^2} = 4{a^2}\,\,\left( 1 \right)\)
Giả sử: \(\left( H \right):\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Vì \(M\left( {\sqrt {10} ;6} \right) \in \left( H \right)\) nên \(\frac{{10}}{{{a^2}}} - \frac{{36}}{{{b^2}}} = 1 \Leftrightarrow 10{b^2} - 36{a^2} = {a^2}{b^2}\,\,\,\left( 2 \right)\)
Thay (1) vào (2) ta được: \(40{a^2} - 36{a^2} = {a^2}.4{a^2} \Rightarrow {a^2} = 1,{b^2} = 4\)
Vậy (H): \(\frac{{{x^2}}}{1} - \frac{{{y^2}}}{4} = 1\)
Bài 40 trang 109 SGK Hình học 10 nâng cao
Chứng minh rằng tích các khoảng cách từ một điểm bất kì thuộc hypebol đến hai đường tiệm cận của nó là một số không đổi.
Hướng dẫn giải:
Giả sử (H) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Phương trình tiệm cận của (H) là \({d_1}:y = \frac{b}{a}x \Leftrightarrow bx - ay = 0\)
\({d_2}:y = - \frac{b}{a}x \Leftrightarrow bx + ay = 0\)
Gọi M(x0;y0) ∈ (H) ta có \(\frac{{x_0^2}}{{{a^2}}} - \frac{{y_0^2}}{{{b^2}}} = 1 \Leftrightarrow {b^2}x_0^2 - {a^2}y_0^2 = {a^2}{b^2}\)
Ta có: \(d\left( {M,{d_1}} \right).d\left( {M,{d_2}} \right) = \frac{{\left| {b{x_0} - a{y_0}} \right|}}{{\sqrt {{a^2} + {b^2}} }}.\frac{{\left| {b{x_0} + a{y_0}} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
\( = \frac{{\left| {{b^2}x_0^2 - {a^2}y_0^2} \right|}}{{{a^2} + {b^2}}} = \frac{{{a^2}{b^2}}}{{{a^2} + {b^2}}}\) không đổi
Bài 41 trang 109 SGK Hình học 10 nâng cao
Trong mặt phẳng tọa độ cho hai điểm \({F_1}\left( { - \sqrt 2 ; - \sqrt 2 } \right),{F_2}\left( {\sqrt 2 ;\sqrt 2 } \right)\). Chứng minh rằng với mỗi điểm M(x, y) nằm trên đồ thị hàm số \(y = \frac{1}{x}\), ta đều có
\(M{F_1}^2 = {\left( {x + \frac{1}{x} + \sqrt 2 } \right)^2};M{F_2}^2 = {\left( {x + \frac{1}{x} - \sqrt 2 } \right)^2}\)
Từ đó suy ra \(\left| {M{F_1} - M{F_2}} \right| = 2\sqrt 2 \)
Hướng dẫn giải:
Giả sử \(M\left( {x;y} \right) \in \left( H \right):y = \frac{1}{x}\), ta có:
\(\begin{array}{l}
M{F_1}^2 = {\left( {x + \sqrt 2 } \right)^2} + {\left( {\frac{1}{x} + \sqrt 2 } \right)^2}\\
= {x^2} + 2\sqrt 2 x + 2 + \frac{1}{{{x^2}}} + 2\sqrt 2 .\frac{1}{x} + 2\\
= \left( {{x^2} + \frac{1}{{{x^2}}} + 2} \right) + 2\sqrt 2 \left( {x + \frac{1}{x}} \right) + 2\\
= {\left( {{x^2} + \frac{1}{x}} \right)^2} + 2\left( {x + \frac{1}{x}} \right).\sqrt 2 + {\left( {\sqrt 2 } \right)^2}\\
= {\left( {x + \frac{1}{x} + \sqrt 2 } \right)^2}\\
MF_2^2 = {\left( {x - \sqrt 2 } \right)^2} + {\left( {\frac{1}{x} - \sqrt 2 } \right)^2}\\
= {\left( {x + \frac{1}{x}} \right)^2} - 2\sqrt 2 \left( {x + \frac{1}{x}} \right) + 2\\
= {\left( {x + \frac{1}{x} - \sqrt 2 } \right)^2}
\end{array}\)
Từ đó suy ra:
- Với x > 0 thì \(x + \frac{1}{x} \ge 2\) (theo bất đẳng thức cô si)
Khi đó: \(M{F_1} = x + \frac{1}{x} + \sqrt 2 ;M{F_2} = x + \frac{1}{x} - \sqrt 2 \)
⇒ \(\left| {M{F_1} - M{F_2}} \right| = 2\sqrt 2 \)
- Với x < 0 thì \(\left| {x + \frac{1}{x}} \right| = \left| x \right| + \frac{1}{{\left| x \right|}} \ge 2 \Rightarrow x + \frac{1}{x} \le - 2\)
Khi đó: \(M{F_1} = - x - \frac{1}{x} - \sqrt 2 ;M{F_2} = - x - \frac{1}{x} + \sqrt 2 \)
⇒ \(M{F_1} - M{F_2} = - 2\sqrt 2 \)
Vậy \(\left| {M{F_1} - M{F_2}} \right| = 2\sqrt 2 \)
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 3 Bài 6 Đường hypebol và góc bất kì với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.
