Bài 42 trang 112 SGK Hình học 10 nâng cao
Trong các câu sau, câu nào đúng, câu nào sai?
a) y2 = −2x là phương trình chính tắc của parabol.
b) y = x2 là phương trình chính tắc của parabol.
c) Parabol (P): y2 = 2x có tiêu điểm F(5;0) và có đường chuẩn Δ: x+0,5 = 0.
d) Parabol y2 = 2px (p > 0) có tiêu điểm F(p;0) và có đường chuẩn Δ: x+p = 0.
Hướng dẫn giải:
Mệnh đề đúng: c)
Các mệnh đề sai: a), b), d).
Bài 43 trang 112 SGK Hình học 10 nâng cao
Viết phương trình chính tắc của parabol (P) trong mỗi trường hợp sau
a) (P) có tiêu điểm F(3;0)
b) (P) đi qua điểm M(1;-1)
c) (P) có tham số tiêu là \(p = \frac{1}{3}\).
Hướng dẫn giải:
Câu a:
Ta có \(\frac{p}{2} = 3 \Rightarrow p = 6\)
Phương trình chính tắc của (P) là: y2 = 12x.
Câu b:
Giả sử (P): y2 = 2px (p > 0)
M(1;−1) ∈ (P) nên \({\left( { - 1} \right)^2} = 2p.1 \Rightarrow p = \frac{1}{2}\)
Vậy (P):y2 = x
Câu c:
(P) có tham số tiêu là \(p = \frac{1}{3}\)
Vậy parabol có phương trình \({y^2} = \frac{2}{3}x\)
Bài 44 trang 112 SGK Hình học 10 nâng cao
Cho parabol y2 = 2px. Tìm độ dài dây cung của parabol vuông góc với trục đối xứng tại tiêu điểm của parabol (dây cung của parabol là đoạn thẳng nối hai điểm của parabol).
Hướng dẫn giải:
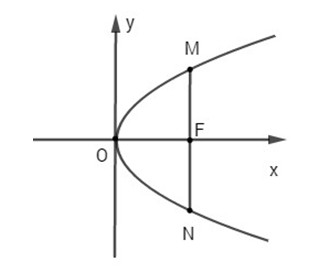
Ta có: \(F\left( {\frac{p}{2};0} \right)\)
Gọi M là điểm thuộc (P) có hoành độ \(x = \frac{p}{2}\), thay \(x = \frac{p}{2}\) vào phương trình của (P) ta được:
\({y^2} = 2p.\frac{p}{2} = {p^2} \Rightarrow y = \pm p\)
Vậy \(M\left( {\frac{p}{2};p} \right)\) và \(N\left( {\frac{p}{2}; - p} \right)\), do đó MN = 2p.
Bài 45 trang 112 SGK Hình học 10 nâng cao
Cho dây cung AB đi qua tiêu điểm của parabol (P). Chứng minh rằng khoảng cách từ trung điểm I của dây AB đến đường chuẩn của (P) bằng \(\frac{1}{2}AB\). Từ đó có nhận xét gì về đường tròn đường kính AB?
Hướng dẫn giải:
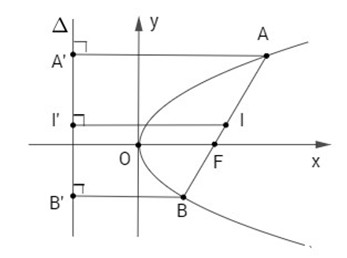
Gọi A′, B′, I′ lần lượt là hình chiếu vuông góc của A, B, I lên đường chuẩn Δ
Theo định nghĩa parabol ta có:
AA′ = AF và BB′ = BF
\(\begin{array}{l}
\Rightarrow AB = AF + FB = AA' + BB' = 2II'\\
\Rightarrow II' = d\left( {I,\Delta } \right) = \frac{{AB}}{2}
\end{array}\)
Từ đó suy ra đường tròn đường kính AB tiếp xúc với đường chuẩn.
Bài 46 trang 112 SGK Hình học 10 nâng cao
Trong mặt phằng tọa độ Oxy cho điểm F(1; -2). Tìm hệ thức giữa x, y để điểm M(x;y) cách đều điểm F và trục hoành.
Hướng dẫn giải:
Phương trình đường thẳng Ox là y = 0
Ta có \(MF = d\left( {M,Ox} \right) \Leftrightarrow \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 2} \right)}^2}} = \left| y \right|\)
\(\begin{array}{l}
\Leftrightarrow {x^2} - 2x + 1 + {y^2} + 4y + 4 = {y^2}\\
\Leftrightarrow y = - \frac{1}{4}{x^2} + \frac{1}{2}x - \frac{5}{4}
\end{array}\)
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 3 Bài 7 Đường parabol và góc bất kì với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.
