Bài 36 trang 96 SGK Toán 10 nâng cao
Cho một hệ hai phương trình bậc nhất hai ẩn. Biết rằng phương trình thứ hai trong hệ vô nghiệm. Hãy chọn kết luận đúng trong các khẳng định sau:
(A) Hệ đã cho nghiệm đúng với mọi giá trị của ẩn;
(B) Hệ đã cho vô nghiệm;
(C) Tập nghiệm của hệ đã cho trùng với tập nghiệm của phương trình thứ nhất;
(D) Không có kết luận gì.
Hướng dẫn giải:
Hệ đã cho vô nghiệm
Chọn (B)
Bài 37 trang 97 SGK Toán 10 nâng cao
Tính nghiệm gần đúng của hệ phương trình sau (chính xác đến hàng phần trăm):
a)
b)
Hướng dẫn giải:
Câu a:
Ta có:
Hệ phương trình có nghiệm duy nhất (x;y) với:
Câu b:
Ta có:
Hệ có nghiệm duy nhất là:
Bài 38 trang 97 SGK Toán 10 nâng cao
Một miếng đất hình chữ nhật có chu vi 2p (mét). Nếu mở rộng miếng đất đó bằng cách tăng một cạnh thêm 3m và cạnh kia thêm 2m thì diện tích miếng đất tăng thêm 246 m2. Tính các kích thước của miếng đất đó (biện luận theo p).
Hướng dẫn giải:
Gọi hai kích thước hình chữ nhật là x và y (x > 0; y > 0)
Ta có hệ phương trình:
Ta có
Vậy kích thước của miếng đất là 3p - 240 (mét) và 240 - 2p (mét) với điều kiện 80 < p < 120.
Bài 39 trang 97 SGK Toán 10 nâng cao
Giải và biện luận các hệ phương trình
a)
b)
Hướng dẫn giải:
Câu a:
Ta có:
- Nếu D ≠ 0 ⇔ m ≠ 0 và m ≠ -3 nên hệ có nghiệm duy nhất là:
- Nếu D = 0
i) Với m = 0, Dy = 3 ≠ 0: hệ vô nghiệm
ii) Với m = - 3, hệ trở thành:
Hệ có vô số nghiệm dạng
Câu b:
Ta có:
- Nếu D ≠ 0 ⇔ m ≠ -1 và m ≠ 2 nên hệ có nghiệm duy nhất là:
- Nếu D = 0 ⇔ m = -1 hoặc m = 2
i) m = -1; Dx ≠ 0. Hệ vô nghiệm
ii) m = 2, thế y = 2 – 2x. Hệ có vô số nghiệm (x; 2 – 2x); x ∈ R
Bài 40 trang 97 SGK Toán 10 nâng cao
Với giá trị nào của a thì mỗi hệ phương trình sau có nghiệm?
a)
b)
Hướng dẫn giải:
Câu a:
Ta có:
Hệ có nghiệm trong hai trường hợp sau:
- Hệ có nghiệm duy nhất, tức là D ≠ 0 (xảy ra khi và chỉ khi a ≠ 0) (nếu a = 0 thì hệ vô nghiệm (do Dx ≠ 0))
- Hệ có vô số nghiệm, tức là D = Dx = Dy = 0 (không xảy ra).
Câu b:
Ta có:
- Nếu a ≠ - 1 và a ≠ - 5 thì hệ có nghiệm duy nhất
- Nếu a = - 1 thì Dy = - 4 ≠ 0: hệ vô nghiệm
- Nếu a = - 5 thì hệ thành:
Hệ có vô số nghiệm (x, x – 2) ∈ R
Vậy hệ có nghiệm khi a ≠ 1
Bài 41 trang 97 SGK Toán 10 nâng cao
Tìm tất cả các cặp số nguyên (a, b) sao cho hệ phương trình sau vô nghiệm:
Hướng dẫn giải:
Ta có
Hệ vô nghiệm thì D = 0 ⇒ ab = 6
Vì a, b ∈ Z nên (a, b) là một trong 8 cặp số nguyên là:
(1, 6); (-1, -6); (6, 1); (-6, -1); (2, 3); (-2, -3); (3, 2); (-3, -2)
Lần lượt thay (a, b) bởi một trong 8 cặp số trên, ta thấy cặp (a, b) = (3, 2) không thỏa mãn yêu cầu bài toán.
Vậy có 7 cặp số thỏa mãn yêu cầu bài toán.
Bài 42 trang 97 SGK Toán 10 nâng cao
Cho hai đường thẳng (d1): x + my = 3 và (d2): mx + 4y = 6.
a) Với giá trị nào của m thì hai đường thẳng đó cắt nhau?
b) Với giá trị nào của m thì hai đường thẳng ấy song song với nhau?
c) Với giá trị nào của m thì hai đường thẳng ấy trùng nhau?
Hướng dẫn giải:
Xét hệ phương trình:
Câu a:
(d1) và (d2) cắt nhau ⇔ D ≠ 0 ⇔ m ≠ ± 2
Câu b:
(d1) // (d2) ⇔ D = 0 và Dx ≠ 0 hoặc (Dy ≠ 0) ⇔ m = - 2
Câu c:
(d1) trùng với (d2) ⇔ D = Dx = Dy = 0 ⇔ m = 2
Bài 43 trang 97 SGK Toán 10 nâng cao
Giải hệ phương trình
Hướng dẫn giải:
Cộng vế với vế phương trình (1) và phương trình (2) ta được phương trình 2x = 8 hay x = 4.
Cộng vế với vế phương trình (2) và phương trình (3) ta có 2y = 4 hay y = 2.
Cộng vế với vế phương trình (1) với phương trình (3) ta có 2z = 10 hay z = 5.
Vậy hệ đã cho có nghiệm (x; y; z) = (4; 2; 5).
Bài 44 trang 97 SGK Toán 10 nâng cao
Bài toán máy bơm nước.
Một gia đình muốn mua một chiếc máy bơm nước. Có hai loại có cùng lưu lượng nước bơm được trong một giờ: loại thứ nhất giá 1,5 triệu đồng, loại thứ hai giá 2 triệu đồng. Tuy nhiên, nếu dùng máy bơm loại thứ nhất thì mồi giờ tiền điện phải trả là 1200 đồng, trong khi dùng máy bơm loại thứ hai thì phải trả 1000 đồng, cho mỗi giờ bơm.
Kí hiệu f(x) và g(x) lần lượt là số tiền (tính bằng nghìn đồng) phải trả khi sử dụng máy bơm loại thứ nhất và loại thứ hai trong X giờ (bao gồm tiền điện và tiền mua máy bơm).
a) Hãy biểu diễn f(x) và g(x) dưới dạng các biểu thức của X.
b) Vẽ đồ thị của y = f(x) và y = g(x) trên cùng một mặt phẳng tọa độ.
c) Xác định tọa độ giao điểm của hai đồ thị ấy. Hãy phân tích ý nghĩa kinh tế của giao điểm đó.
Hướng dẫn giải:
Câu a:
Ta có:
1,5 triệu = 1500 nghìn
2 triệu = 2000 nghìn
1200 = 1,2 nghìn
Theo đề bài ta có:
f(x) =1500 + 1,2x
g(x) = 2000 + x
Câu b:
Đồ thị
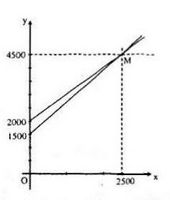
Câu c:
Hoành độ giao điểm M của hai đồ thị là nghiệm của phương trình f(x) = g(x), tức là:
1500 + 1,2x = 2000 + x
Phương trình này có nghiệm duy nhất là x = 2500.
Tung độ của M là g(2500) = 4500
Vậy tọa độ của M là (2500;4500)
Ta thấy: Khi x > 2500 thì đường thẳng y = f(x) ở phía trên đường thẳng y = g(x)
Từ đó, suy ra ý nghĩa kinh tế của điểm M như sau:
- Nếu dùng đúng 2500 giờ bơm thì số tiền phải trả (tiền điện và tiền máy bơm cho hai máy bơm là như nhau (và bằng 4500 nghìn đồng)
- Nếu dùng ít hơn 2500 giờ bơm thì mua máy thứ nhất sẽ tiết kiệm hơn.
- Nếu dùng nhiều hơn 2500 giờ bơm thì mua máy thứ hai tiết kiệm hơn.
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 3 Luyện tập (trang 96, 97) Hệ phương trình bậc nhất nhiều ẩn với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.






Thảo luận về Bài viết