Giải Toán 10 SGK nâng cao Chương 3 Bài 4 Hệ phương trình bậc nhất nhiều ẩn

Cho hệ phương trình bậc nhất hai ẩn. Biết rằng phương trình thứ hai trong hệ nghiệm đúng với mọi giá trị của các ẩn. Hãy chọn kết luận đúng trong các khẳng định sau:

(A) Hệ đã cho nghiệm đúng với mọi giá trị của các ẩn;

(B) Hệ đã cho vô nghiệm;

(C) Tập nghiệm của hệ đã cho trùng với tập nghiệm của phương trình thứ nhất;

(D) Không có kết luận gì.

Hướng dẫn giải:

Tập nghiệm của hệ trùng với tập nghiệm của phương trình bậc nhất.

Kết luận (C) là kết luận đúng.

---

Bằng định thức, giải các phương trình sau:

a) \(\left\{ \begin{array}{l}
5x - 4y = 3\\
7x - 9y = 8
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
\sqrt 3 x + \sqrt 2 y =  - 1\\
2\sqrt 2  + \sqrt 3 y = 0
\end{array} \right.\) 

Hướng dẫn giải:

Câu a:

Ta có:

\(\begin{array}{l}
D = \left| {\begin{array}{*{20}{c}}
5&{ - 4}\\
7&{ - 9}
\end{array}} \right| =  - 45 + 28 =  - 17\\
{D_x} = \left| {\begin{array}{*{20}{c}}
3&{ - 4}\\
8&{ - 9}
\end{array}} \right| =  - 27 + 32 = 5\\
{D_y} = \left| {\begin{array}{*{20}{c}}
5&3\\
7&8
\end{array}} \right| = 40 - 21 = 19
\end{array}\)

Vậy hệ có nghiệm là \(\left\{ \begin{array}{l}
x = \frac{{{D_x}}}{D} = \frac{{ - 5}}{{17}}\\
y = \frac{{{D_y}}}{D} = \frac{{ - 19}}{{17}}
\end{array} \right.\)

Câu b:

Ta có:

\(\begin{array}{l}
D = \left| {\begin{array}{*{20}{c}}
{\sqrt 3 }&{\sqrt 2 }\\
{2\sqrt 2 }&{\sqrt 3 }
\end{array}} \right| = 3 - 4 =  - 1\\
{D_x} = \left| {\begin{array}{*{20}{c}}
{ - 1}&{\sqrt 2 }\\
0&{\sqrt 3 }
\end{array}} \right| =  - \sqrt 3 \\
{D_y} = \left| {\begin{array}{*{20}{c}}
{\sqrt 3 }&{ - 1}\\
{2\sqrt 2 }&0
\end{array}} \right| = 2\sqrt 2 
\end{array}\)

Vậy hệ có phương trình là \(\left\{ \begin{array}{l}
x = \frac{{{D_x}}}{D} = \sqrt 3 \\
y = \frac{{{D_y}}}{D} =  - 2\sqrt 2 
\end{array} \right.\)

---

Giải các hệ phương trình sau:

a) \(\left\{ \begin{array}{l}
\frac{4}{x} + \frac{1}{{y - 1}} = 3\\
\frac{2}{x} - \frac{2}{{y - 1}} = 4
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
\frac{{3\left( {x + y} \right)}}{{x - y}} =  - 7\\
\frac{{5x - y}}{{y - x}} = \frac{5}{3}
\end{array} \right.\)

Hướng dẫn giải: 

Câu a:

Điều kiện: \(x \ne 0,y \ne  - 1\)

Đặt \(X = \frac{1}{x};Y = \frac{1}{{y - 1}}\)

Ta có hệ phương trình:

\(\begin{array}{l}
\left\{ \begin{array}{l}
4X + Y = 3\\
2X - 2Y = 4
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
X = 1\\
Y =  - 1
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
\frac{1}{x} = 1\\
\frac{1}{{y - 1}} =  - 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 1\\
y = 0
\end{array} \right.
\end{array}\)

Vậy hệ phương trình có nghiệm (1;0)

Câu b:

Điều kiện: \(x \ne y\)

Ta có:

\(\begin{array}{l}
\left\{ \begin{array}{l}
\frac{{3\left( {x + y} \right)}}{{x - y}} =  - 7\\
\frac{{5x - y}}{{y - x}} = \frac{5}{3}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
3\left( {x + y} \right) =  - 7\left( {x - y} \right)\\
3\left( {5x - y} \right) = 5\left( {y - x} \right)
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
10x - 4y = 0\\
20x - 8y = 0
\end{array} \right. \Leftrightarrow y = \frac{5}{2}x
\end{array}\)

Vậy hệ có vô số nghiệm \(\left( {x;\frac{5}{2}x} \right)\) với \(x \in R\backslash \left\{ 0 \right\}\) (do \(x \ne y\))

---

Giải và biện luận hệ phương trình

a) \(\left\{ \begin{array}{l}
x - my = 0\\
mx - y = m + 1
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
2ax + 3y = 5\\
\left( {a + 1} \right)x + y = 0
\end{array} \right.\)

Hướng dẫn giải: 

Câu a:

Ta có:

\(\begin{array}{*{20}{l}}
{D = \left| {\begin{array}{*{20}{c}}
1&{ - m}\\
m&{ - 1}
\end{array}} \right| = {m^2} - 1}\\
{{D_x} = \left| {\begin{array}{*{20}{c}}
0&{ - m}\\
{m + 1}&{ - 1}
\end{array}} \right| = m\left( {m + 1} \right)}\\
{{D_y} = \left| {\begin{array}{*{20}{c}}
1&0\\
m&{m + 1}
\end{array}} \right| = m + 1}
\end{array}\)

• Với D ≠  0 ⇔ m ≠ ± 1 thì hệ có nghiệm duy nhất:

\(\left\{ \begin{array}{l}
x = \frac{{{D_x}}}{D} = \frac{{m\left( {m + 1} \right)}}{{{m^2} - 1}} = \frac{m}{{m - 1}}\\
y = \frac{{{D_y}}}{D} = \frac{{m + 1}}{{{m^2} - 1}} = \frac{1}{{m - 1}}
\end{array} \right.\)

• Với D = 0 ⇔ m = ± 1

i) m = 1, ta có D_x = 2 ≠ 0: Hệ phương trình vô nghiệm

ii) m = - 1. Hệ trở thành: 

\(\left\{ \begin{array}{l}
x + y = 0\\
 - x - y = 0
\end{array} \right. \Leftrightarrow y =  - x\)

Hệ vô số nghiệm (x; - x) với x ∈ R

Câu b:

Ta có:

\(\begin{array}{l}
D = \left| {\begin{array}{*{20}{c}}
{2a}&3\\
{a + 1}&1
\end{array}} \right| = 2a - 3\left( {a + 1} \right) =  - \left( {a + 3} \right)\\
{D_x} = \left| {\begin{array}{*{20}{c}}
5&3\\
0&1
\end{array}} \right| = 5\\
{D_y} = \left| {\begin{array}{*{20}{c}}
{2a}&5\\
{a + 1}&0
\end{array}} \right| =  - 5\left( {a + 1} \right)
\end{array}\)

• Nếu \(a \ne  - 3\) thì hệ có nghiệm duy nhất:

\(\left\{ \begin{array}{l}
x = \frac{{{D_x}}}{D} = \frac{{ - 5}}{{a + 3}}\\
y = \frac{{{D_y}}}{D} = \frac{{5\left( {a + 1} \right)}}{{a + 3}}
\end{array} \right.\)

• Nếu \(a=-3\) thì hệ vô nghiệm (do D = 0)

---

Giải hệ phương trình sau ( có thể dùng máy tính bỏ túi để kiểm tra kết quả - Xem bài đọc thêm trang 94)

\(\left\{ \begin{array}{l}
x + y + z = 11\\
2x - y + z = 5\\
3x + 2y + z = 24
\end{array} \right.\)

Hướng dẫn giải: 

Lấy (1) trừ (2), ta được \(-x+2y=6\)

Lấy (2) trừ (3), ta được \(-x-3y=-19\)

Ta có hệ:

\(\left\{ \begin{array}{l}
x - 2y =  - 6\\
x + 3y = 19
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 4\\
y = 5
\end{array} \right.\)

Thay \(x=4, y=5\) vào (1) ta được \(z=2\)

Vậy hệ có nghiệm (4;5;2)

---

Cho một mạch điện kín. Biết R₁ = 0,250, R₂ = 0,360, R₃ = 0,450 và U = 0,6V. Gọi I₁ là cường độ dòng điện của mạch chính, I₂ và I₃ là cường độ dòng diện của mạch rẽ. Tính I₁, I₂, I₃ (chính xác đến phần trăm).

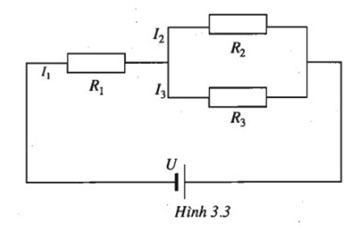
Hướng dẫn giải: 

Ta có hệ phương trình ẩn I₁, I₂, I₃:

\(\begin{array}{l}
\left\{ \begin{array}{l}
{I_1} = {I_2} + {I_3}\\
{R_1}{I_1} + {R_2}{I_2} = U\\
{R_2}{I_2} = {R_3}{I_3}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{I_1} - {I_2} - {I_3} = 0\\
0,25{I_1} + 0,36{I_2} = 0,6\\
0,36{I_2} - 0,45{I_3} = 0
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
{I_1} \approx 1,33A\\
{I_2} \approx 0,74A\\
{I_3} \approx 0,59A
\end{array} \right.
\end{array}\)

 

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 3 Bài 4 Hệ phương trình bậc nhất nhiều ẩn với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.