Bài tập trắc nghiệm Toán 9 Bài 5: Góc có đỉnh ở bên trong đường tròn Góc có đỉnh ở bên ngoài đường tròn.
Câu hỏi trắc nghiệm (5 câu):
-
Câu 1:
Dựa vào hình vẽ sau, biết B là điểm chính giữa cung nhỏ AC, M là giao điểm của AD và BE và sđ
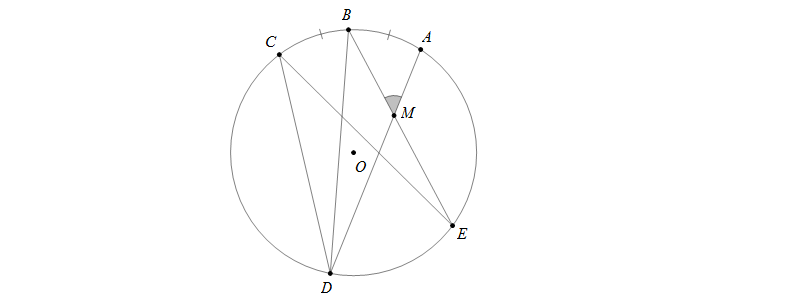
- A.900
- B.600
- C.450
- D.500
-
Câu 2:
Khẳng nào sau đây là đúng:
- A.Số đo của góc có đỉnh bên trong đường tròn bằng nửa hiệu số đo hai cung bị chắn.
- B.Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa tổng số đo hai cung bị chắn.
- C.Góc có đỉnh trên đường tròn được gọi là góc nội tiếp và bằng góc ở tâm cùng chắn cung đó.
- D.Góc nội tiếp chắn nửa đường tròn là góc vuông.
-
Câu 3:
Số đo góc AED là bao nhiêu biết rằng
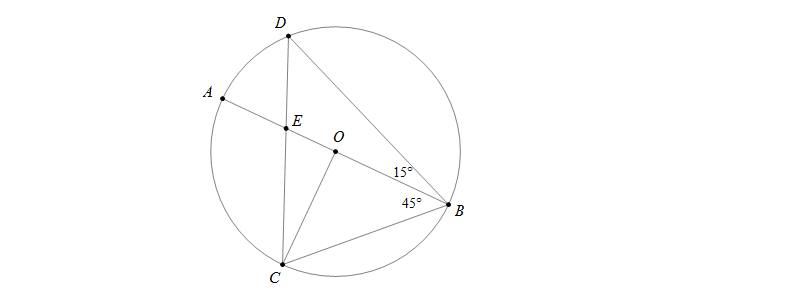
- A.600
- B.700
- C.550
- D.650
-
Câu 4:
Cho đường tròn (O) và điểm E nằm ngoài đường tròn. Vẽ cát tuyến EAB và ECD với đường tròn (A nằm giữa E và B, C nằm giữa E và D). Gọi F là một điểm trên đường tròn sao cho B nằm chính giữa cung DF, I là giao điểm của FA và BC. Biết
- A.350
- B.150
- C.500
- D.250
-
Câu 5:
Cho đường tròn (O) và hai dây AB,CD của đường tròn sao cho AB cắt CD tại E. I là giao điểm của AD và BC. Cho
- A.750
- B.850
- C.1000
- D.1100






Thảo luận về Bài viết