Bài tập trắc nghiệm Toán 12 Ôn tập chương 3 Nguyên hàm, Tích phân và Ứng dụng.
Câu hỏi trắc nghiệm (20 câu):
-
Câu 1:
Hàm số nào sau đây không phải làm nguyên hàm của hàm số \(f(x) = 2\sin 2x.\)
- A.\(F(x) = 2{\sin ^2}x\)
- B.\(F(x) = - 2{\cos ^2}x\)
- C.\(F(x) = - 1 - \cos 2x\)
- D.\(F(x) = - 1 - 2\cos x\sin x\)
-
Câu 2:
Biết \(F\left( x \right) = \left( {ax + b} \right).{e^x}\) là nguyên hàm của hàm số \(y = \left( {2x + 3} \right).{e^x}.\) Tính tổng a + b.
- A.a+b=2
- B.a+b=3
- C.a+b=4
- D.a+b=5
-
Câu 3:
Trong các tích phân sau, tích phân nào không có cùng giá trị với \(I = \int\limits_1^2 {{x^3}\sqrt {{x^2} - 1} dx} .\)
- A.\(\frac{1}{2}\int_1^2 {t\sqrt {t - 1} dt}\)
- B.\(\frac{1}{2}\int_1^4 {t\sqrt {t - 1} dt}\)
- C.\(\int_0^{\sqrt 3 } {\left( {{t^2} + 1} \right){t^2}dt}\)
- D.\(\int_0^{\sqrt 3 } {\left( {{x^2} + 1} \right){x^2}dx}\)
-
Câu 4:
Tính diện tích S của hình phẳng được giới hạn bởi các đồ thị hàm số \(y=x^2\) và \(y=x\).
- A.\(S=\frac{1}{2}\) (đvdt)
- B.\(S=\frac{1}{3}\) (đvdt)
- C.\(S=\frac{1}{4}\) (đvdt)
- D.\(S=\frac{1}{6}\) (đvdt)
-
Câu 5:
Biết rằng \(\int\limits_1^5 {\frac{3}{{{x^2} + 3x}}dx} = a\ln 5 + b\ln 2, \left( {a,b \in Z } \right).\) Mệnh đề nào sau đây đúng?
- A. a + 2b = 0
- B.a + b = 0
- C.a - b = 0
- D.2a - b = 0
-
Câu 6:
Có bao nhiêu số nguyên dương n sao cho biểu thức \(P = n\ln n - \int_1^n {\ln xdx}\) có giá trị không vượt quá 2017.
- A.2017
- B.2018
- C.4034
- D.4036
-
Câu 7:
Tính thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = 0,\,y = x\sqrt {\ln (x + 1)}\) và x = 1 xung quanh trục Ox.
- A.\(V = \frac{\pi }{{18}}(12\ln 2 - 5)\)
- B.\(V = \frac{{5\pi }}{{18}}\)
- C.\(V = \frac{{5\pi }}{{6}}\)
- D.\(V = \frac{\pi }{6}(12\ln 2 - 5)\)
-
Câu 8:
Cho \(I = \int\limits_0^1 {f\left( {\frac{{\sqrt x }}{{\sqrt x + \sqrt {1 - x} }}} \right)dx} = 10\). Tính \(J = \int\limits_0^1 {f\left( {\frac{{\sqrt {1 - x} }}{{\sqrt x + \sqrt {1 - x} }}} \right)dx}.\)
- A.J=10
- B.J=-10
- C.J=-9
- D.J=9
-
Câu 9:
Cho hàm số \(f(x) = \frac{a}{{{{(x + 1)}^3}}} + bx{e^x}.\) Tìm a và b biết rằng \(f'(x) = - 22\) và \(\int\limits_0^1 {f(x)dx = 5.}\)
- A.\(a = - 2;b = - 8\)
- B.\(a = 2;b =8\)
- C.\(a =8;b =2\)
- D.\(a =-8;b =-2\)
-
Câu 10:
Từ khúc gỗ hình trụ có bán kính 30cm, người ta cắt khúc gỗ bởi một mặt phẳng đi qua đường kính và nghiêng với đáy một góc \(45^0\) để lấy một hình nêm như hình vẽ.
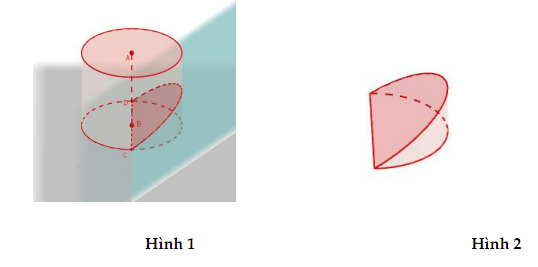
Kí hiệu V là thể tích của hình nêm (Hình 2). Tìm V.
- A.\(V = 2250\,(c{m^3})\)
- B.\(V = \frac{{225\pi }}{4}(c{m^3})\)
- C.\(V = 1250\,(c{m^3})\)
- D.\(V = 1350\,(c{m^3})\)
-
Câu 11:
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x2 và y = 2x là:
- A.\(\frac{4}{3}\)
- B.\(\frac{3}{2}\)
- C.\(\frac{5}{3}\)
- D.\(\frac{{23}}{{15}}\)
-
Câu 12:
Diện tích hình phẳng giới hạn bởi y = (e + 1)x và y = (1 + ex)x là:
- A.\(1 - \frac{e}{2}\)
- B.\(\frac{e}{2} - 1\)
- C.\(e - 1\)
- D.\(1-e\)
-
Câu 13:
Diện tích hình phẳng giới hạn bởi y = (x - 6)2 và y = 6x - x2 là:
- A.9
- B.\(\frac{9}{2}\)
- C.0
- D.Kết quả khác
-
Câu 14:
Tìm \(I = \int {\frac{{{{\cos }^3}x}}{{1 + \sin x}}dx} \)
- A.\(I = - \frac{1}{2}{\sin ^2}x + \sin x + C\)
- B.\(\frac{1}{2}{\sin ^2}x + \sin x + C\)
- C.\(I = {\sin ^2}x - \sin x + C\)
- D.\(I = - \frac{1}{2}{\sin ^2}x - \sin x + C\)
-
Câu 15:
Diện tích hình phẳng giới hạn bởi đường cong: y = x2 + 1, tiếp tuyến với đường cong này tại M(2;5) và trục Oy là:
- A.0
- B.\( - \frac{8}{3}\)
- C.\( \frac{8}{3}\)
- D.Kết quả khác
-
Câu 16:
Thể tích vật thể tròn xoay sinh ra bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi trục Ox và \(y = \sqrt x \sin x\) với (0 ≤ x ≤ π) là:
- A.\( - \frac{{{\pi ^2}}}{4}\)
- B.\( \frac{{{\pi ^2}}}{4}\)
- C.\(\frac{{{\pi ^2}}}{2}\)
- D.\(-\frac{{{\pi ^2}}}{2}\)
-
Câu 17:
Tính thể tích vật thể tròn xoay quanh trục Ox sinh bởi hình phẳng giới hạn bởi các đường \(y = 0,y = \sqrt {{\rm{co}}{{\rm{s}}^6}x + {{\sin }^6}x} ,x = 0,x = \frac{\pi }{2}\)
- A.\( - \frac{{11{\pi ^2}}}{{16}}\)
- B.\( \frac{{11{\pi ^2}}}{{16}}\)
- C.\(\frac{{{\pi ^2}}}{8}\)
- D.\(\frac{{{\pi ^2}}}{8}\)
-
Câu 18:
Tính thể tích vật thể tròn xoay quanh trục Oy sinh bởi hình phẳng giới hạn bởi các đường y = 2, y = 4, \(y = \frac{{{x^2}}}{2}\)
- A.\(12\pi \)
- B.\(-12\pi \)
- C.\(16\pi \)
- D.\(-16\pi \)
-
Câu 19:
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = tanx, y = 0, x = 0, x = \(\frac{\pi }{3}\) quanh Ox là:
- A.\(\sqrt 3 - \frac{\pi }{3}\)
- B.\(\frac{\pi }{3} - 3\)
- C.\(\frac{{{\pi ^2}}}{3} - \pi \sqrt 3 \)
- D.\(\pi \sqrt 3 - \frac{{{\pi ^2}}}{3}\)
-
Câu 20:
Một vật chuyển động với vận tốc \(v\left( t \right) = 1,2 + \frac{{{t^2} + 4}}{{t + 3}}\left( {m/s} \right)\). Quãng đường vật đi được sau 4s xấp xỉ bằng:
- A.11m
- B.12m
- C.13m
- D.14m
