Bài tập SGK Toán 6 Bài 5: Vẽ góc cho biết số đo.
-
Bài tập 24 trang 84 SGK Toán 6 Tập 2
Vẽ góc xBy có số đo bằng 450
Hướng dẫn: Vẽ tia Bx, sau đó trên một nửa mặt bẳng có bờ chứa tia Bx vẽ tia By sao cho = 450 -
Bài tập 25 trang 84 SGK Toán 6 Tập 2
Vẽ góc IKM có số đo bằng 1350
-
Bài tập 26 trang 84 SGK Toán 6 Tập 2
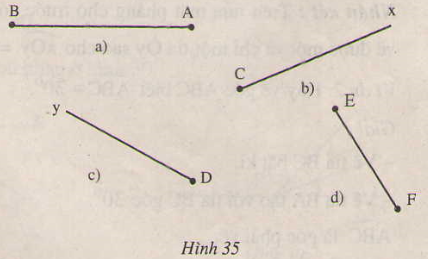
Vẽ góc cho biết một cạnh và số đo góc đó trong bốn trường hợp sau(h.35)
a)
b)
c)
d)
-
Bài tập 27 trang 85 SGK Toán 6 Tập 2
Trên cùng một mặt phẳng bờ chứa tia OA, vẽ hai tia OB, OC sao cho
Tính số đo góc BOC.
-
Bài tập 28 trang 85 SGK Toán 6 Tập 2
Trên mặt phẳng, cho tia Ax. Có thể vẽ được mấy tia Ay sao cho
-
Bài tập 29 trang 85 SGK Toán 6 Tập 2
Gọi Ot, Ot' là hai tia nằm trên cùng một nửa mặt phẳng bờ là đường thẳng xy đi qua O. Biết
-
Bài tập 24 trang 89 SBT Toán 6 Tập 2
Vẽ góc xOl có số đo bằng 400
-
Bài tập 25 trang 89SBT Toán 6 Tập 2
Vẽ góc vuông BAC.
Hướng dẫn:
Cách 1: Dùng thước đo góc.
Cách 2: Dùng êke
-
Bài tập 26 trang 89 SBT Toán 6 Tập 2
So sánh hai góc ở hình dưới.
Hướng dẫn:
Cách 1: Đo riêng từng góc rồi so sánh hai số đó
Cách 2: Vẽ lại hai góc lên giấy trong. Đặt chồng hai góc sao cho đỉnh trùng nhau, một cạnh trùng nhau, hai cạnh còn lại của hai góc nằm cùng phía đối với cạnh trùng nhau rồi vận dụng kiến thức bài 5 để kết luận.
-
Bài tập 27 trang 89 SBT Toán 6 Tập 2
Tính tổng số đo hai góc ở hình trong bài 26
Hướng dẫn:
Cách 1: Đo riêng từng góc rồi cộng hai số đo.
Cách 2: Vẽ hai góc ở vị trí kề nhau rồi đo góc tổng
-
Bài tập 28 trang 189 SBT Toán 6 Tập 2
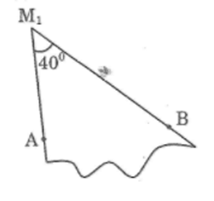
a) Vẽ góc 400 có đỉnh là M trên giấy cứng. Cắt ra ta được một mẫu hình.
b) Đóng hai chiếc đinh vào hai điểm A và B cách nhau 2,5 cm. Đưa mẫu hình vào khe hở giữa hai chiếc đinh sao cho một cạnh sát A, một cạnh sát B. Khi đó đỉnh M của góc ở vị trí M1. Đặt mẫu hình nhiều lần để được nhiều vị trí M1, M2, M3, ... khác nhau của đỉnh M. Vậy ta có:
Đánh dấu khoảng 10 vị trí khác nhau của đỉnh M và dự đoán quỹ đạo của đỉnh M (hình bên)
-
Bài tập 29 trang 90 SBT Toán 6 Tập 2
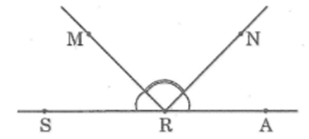
a) Vẽ vào vở hình dưới trong đó ba điểm S, R, A thẳng hàng và
b) Tính
c) Dùng thước đo góc kiểm tra lại kết quả


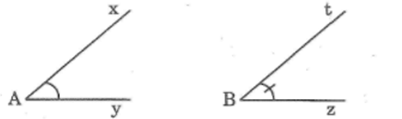




Thảo luận về Bài viết