Bài tập SGK Bài 2: Đồ thị của hàm số y = ax^2 (a ≠ 0)

Bài tập 4 trang 36 SGK Toán 9 Tập 2

Cho hai hàm số: \(y=\frac{3}{2}x^2,y=-\frac{3}{2}x^2\). Điền vào những ô trống của các bảng sau rồi vẽ hai đồ thị trên cùng một mặt phẳng tọa độ.

Nhận xét về tính đối xứng của hai đồ thị đối với trục Ox.

Bài tập 5 trang 37 SGK Toán 9 Tập 2

Cho ba hàm số: \(y=\frac{1}{2}x^2; y = x^2 ; y = 2x^2\)

a) Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.

b) Tìm ba điểm A, B, C có cùng hoành độ x = -1,5 theo thứ tự nằm trên ba đồ thị. Xác định tung độ tương ứng của chúng.

c) Tìm ba điểm A', B', C' có cùng hoành độ x = 1,5 theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của A và A', B và B', C và C'.

d) Với mỗi hàm số trên, hãy tìm giá trị của x để hàm số đó có giá trị nhỏ nhất.

Bài tập 6 trang 38 SGK Toán 9 Tập 2

Cho hàm số \(y = f(x) = x^2\)

a) Vẽ đồ thị của hàm số đó.

b) Tính các giá trị f(-8); f(-1,3); f(-0,75); f(1,5).

c) Dùng đồ thị để ước lượng các giá trị (0,5)²; (-1,5)²; (2,5)².

d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số \(\sqrt{3};\sqrt{7}\).

Bài tập 7 trang 38 SGK Toán 9 Tập 2

Trên mặt phẳng tọa độ (h.10), có một điểm M thuộc đồ thị của hàm số y = ax².

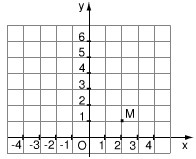
a) Tìm hệ số a

b) Điểm A(4; 4) có thuộc đồ thị không ?

c) Hãy tìm thêm hai điểm nữa (không kể điểm O) để vẽ đồ thị.

Bài tập 8 trang 38 SGK Toán 9 Tập 2

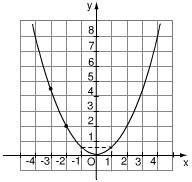
Biết rằng đường cong trong hình 11 là một parabol y = ax² 

a) Tìm hệ số a

b) Tìm tung độ của điểm thuộc parabol có hoành độ x = -3

c) Tìm các điểm thuộc parabol có tung độ y = 8

Bài tập 9 trang 39 SGK Toán 9 Tập 2

Cho hai hàm số \(y = \frac{1}{3}x^2\) và \(y = -x + 6.\)

a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.

b) Tìm tọa độ các giao điểm của hai đồ thì đó.

Bài tập 10 trang 39 SGK Toán 9 Tập 2

Cho hàm số y = -0,75x² . Qua đồ thị của hàm số đó, hãy cho biết khi x tăng từ -2 đến 4 thì giá trị nhỏ nhất và giá trị lớn nhất của y là bao nhiêu?

Bài tập 8 trang 62 SBT Toán 9 Tập 1

Cho hàm số y = (3 - √2 )x + 1

a. Hàm số là hàm đồng biến hay nghịch biến trên R? Vì sao?

b. Tính các giá trị tương ứng của y khi x nhận các giá trị sau:

0; 1; √2 ; 3 + √2 ; 3 - √2

c. Tính các giá trị tương ứng của x khi y nhận các giá trị sau:

0; 1; 8; 2 + √2 ; 2 - √2