Bài tập SGK Bài 10: Phép nhân phân số

Bài tập 69 trang 36 SGK Toán 6 Tập 2

Nhân các phân số (rút gọn nếu có thể):

a) $\frac{-1}{4}.\frac{1}{3}$ ; b) $\frac{-2}{5}.\frac{5}{-9}$ ; c) $\frac{-3}{4}.\frac{16}{7}$ ;

d) $\frac{-8}{3}.\frac{15}{24}$ ; e) $(-5).\frac{8}{15}$ ; g) $\frac{-9}{11}.\frac{5}{18}$ .

Bài tập 70 trang 37 SGK Toán 6 Tập 2

Phân số $\frac{6}{35}$ có thể được viết dưới dạng tích của hai phân số có tử và mẫu số là số nguyên dương có một chữ số.

Chẳng hạn: $\frac{6}{35}=\frac{2}{5}.\frac{3}{7}$. Hãy tìm cách viết khác.

Bài tập 71 trang 37 SGK Toán 6 Tập 2

Tìm x, biết:

a) $x-\frac{1}{4}=\frac{5}{8}.\frac{2}{3}$ ;

b) $\frac{x}{126}=\frac{-5}{9}.\frac{4}{7}$ ;

Bài tập 72 trang 37 SGK Toán 6 Tập 2

Đố: Có những cặp phân số mà khi ta nhân chúng với nhau hoặc cộng chúng với nhau đều được cùng một kết quả.

Chẳng hạn : Cặp phân số $\frac{7}{3}$ và $\frac{7}{4}$ có :

$\frac{7}{3}.\frac{7}{4}=\frac{7.7}{3.4}=\frac{49}{12}$

$\frac{7}{3}+\frac{7}{4}=\frac{7.4+7.3}{3.4}=\frac{49}{12}$.

Đố em tìm được một cặp phân số khác cũng có tính chất ấy.

Bài tập 83 trang 25 SBT Toán 6 Tập 2

Làm tính nhân:

a) $\frac{-1}{3}.\frac{5}{7}$

b) $\frac{-15}{16}.\frac{8}{-25}$

c) $\frac{-21}{24}.\frac{8}{-14}$

Bài tập 84 trang 25 SBT Toán 6 Tập 2

Tính

a) $\frac{-5}{13}.26$

b) ${\left(\frac{-2}{7}\right)}^2$

c) $\left(2-\frac{1}{2}\right).\left(\frac{-3}{4}+\frac{1}{2}\right)$

Bài tập 85 trang 25 SBT Toán 6 Tập 2

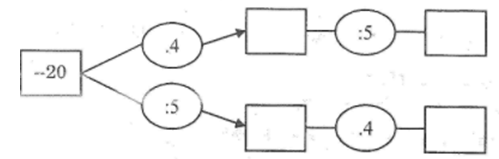
Hoàn thành sơ đồ sau để thực hiện phép nhân $-20.\frac{4}{5}$

Từ cách làm trên , em hãy điền các từ thích hợp vào câu sau:

Khi nhân một số nguyên với một phân số, ta có thể:

- Nhân số đó với ….rồi lấy kết quả ….hoặc

- Chia số đó cho …rồi lấy kết quả ….

Áp dụng:

$\begin{array}{l}a)\left(-15\right).\frac{3}{5}\\ b)42.\frac{-6}{7}\\ c)\left(-26\right).\frac{3}{-13}\\ d)\left(-12\right).\frac{2}{5}\\ e)\left(-17\right).\frac{-3}{52}\end{array}$

Bài tập 86 trang 25 SBT Toán 6 Tập 2

Tính 

$\begin{array}{l}a)\frac{2}{3}+\frac{1}{5}.\frac{10}{7}\\ b)\frac{7}{12}-\frac{27}{7}.\frac{1}{18}\\ c)\left(\frac{23}{41}-\frac{15}{82}\right).\frac{41}{25}\\ d)\left(\frac{4}{5}+\frac{1}{2}\right).\left(\frac{3}{13}-\frac{8}{13}\right)\end{array}$

Bài tập 87 trang 26 SBT Toán 6 Tập 2

a) Cho hai phân số $\frac{1}{n}$ và $\frac{1}{n+1}$ (n ∈ Z, n > 0) . Chứng tỏ rằng tích của phân số này bằng hiệu của chúng

b) Áp dụng kết quả trên để tính các giá trị của biểu thức sau:

$\begin{array}{l}A=\frac{1}{2}.\frac{1}{3}+\frac{1}{3}.\frac{1}{4}+\frac{1}{4}.\frac{1}{5}+\frac{1}{5}.\frac{1}{6}+\frac{1}{6}.\frac{1}{7}+\frac{1}{7}.\frac{1}{8}+\frac{1}{8}.\frac{1}{9}\\ B=\frac{1}{30}+\frac{1}{42}+\frac{1}{56}+\frac{1}{72}+\frac{1}{90}+\frac{1}{110}+\frac{1}{132}\end{array}$

Bài tập 88 trang 26 SBT Toán 6 Tập 2

Cho hai phân số $\frac{a}{b}$ và $\frac{a}{c}$ có b + c = a (a, b, c ∈ Z, b ≠ 0, c ≠ 0). Chứng tỏ rằng tích của hai phân số này bằng tổng của chúng. Thử lại với a = 8; b = -3

Bài tập 10.1 trang 26 SBT Toán 6 Tập 2

$\frac{5}{38}$ là tích của hai phân số nào:

$\begin{array}{l}\left(A\right)\frac{-5}{2}.\frac{1}{-19}\\ \left(B\right)\frac{-5}{-19}.\frac{1}{2}\\ \left(C\right)\frac{5}{-2}.\frac{-1}{19}\\ \left(D\right)\frac{1}{-2}.\frac{5}{19}\end{array}$

Bài tập 10.2 trang 26 SBT Toán 6 Tập 2

Tích $\frac{1}{11}.\frac{1}{12}$ bằng

$\begin{array}{l}\left(A\right)\frac{1}{12}-\frac{1}{11}\\ \left(B\right)\frac{2}{23}\\ \left(C\right)\frac{1}{11}+\frac{1}{12}\\ \left(D\right)\frac{1}{11}-\frac{1}{12}\end{array}$

Hãy chọn đáp số đúng.