Bài tập SGK Toán 8 Bài 6: Diện tích đa giác.
-
Bài tập 37 trang 130 SGK Toán 8 Tập 1
Thực hiện các phép đo cần thiết (chính xác đến từng mm) để tính diện tích hình ABCDE (h.152).
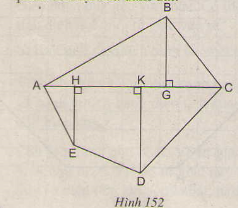
-
Bài tập 38 trang 130 SGK Toán 8 Tập 1
Một con đường cắt một đám đất hình chữ nhật với các dữ liệu được cho trên hình 153. Hãy tính diện tich phần con đường EBGF (EF // BG) và diện tích hần còn lại của đám đất.
.png)
.png)
-
Bài tập 39 trang 131 SGK Toán 8 Tập 1
Thực hiện các phép vẽ và đo cần thiết để tính diện tích một đám đất có dạng như hình 154, trong đó AB // CE và được vẽ tỉ lệ

-
Bài tập 40 trang 131 SGK Toán 8 Tập 1
Tính diện tích thực của hồ nước có sơ đồ là phần gạch sọc trên hình 155 (cạnh của mỗi hình vuông là 1cm, tỉ lệ
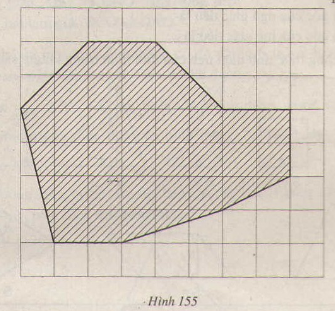
-
Bài tập 47 trang 164 SBT Toán 8 Tập 1
Thực hiện phép vẽ và đo cần thiết để tính diện tích đa giác ABCDE có AE // BC (như hình vẽ).
-
Bài tập 48 trang 164 SBT Toán 8 Tập 1
Theo bản đồ ghi hình bên tỉ lệ 1:100 , hãy tính điện tích hồ nước phần gạch đậm.
-
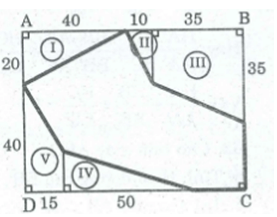
Bài tập 49 trang 164 SBT Toán 8 Tập 1
Theo kích thước đã cho trên hình. Tính diện tích phân gạch đậm (đơn vị là m2)
-
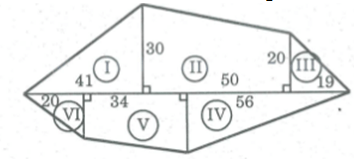
Bài tập 50 trang 164 SBT Toán 8 Tập 1
Tính diện tích mảnh đất theo kích thước trong hình (đơn vị m2)
-
Bài tập 6.1 trang 164 SBT Toán 8 Tập 1
Tính diện tích của hình được cho trong mỗi trường hợp sau đây:
a) Đa giác ABCDEF, biết AD = 4cm, BC = 1cm, FE = 2cm, FB = 3cm, FB vuông góc với AD như hình bs. 24
b) Cho đa giác ABCD, CF và DE đều vuông góc với AB (như hình bs. 25)
Biết AB = 13cm, CF = 8cm, DE = 4cm, FB = 6cm và AE = 3cm. Tính diện tích đa giác ABCD
-
Bài tập 6.2 trang 165 SBT Toán 8 Tập 1
Cho hình bình hành ABCD, với diện tích S và AB = a, AD = b. Lấy mỗi cạnh của hình bình hành đó làm cạnh dựng một hình vuông ra phía ngoài hình bình hành. Tính theo a, b và S diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là cạnh của hình bình hành đã cho.
-
Bài tập 6.3 trang 165 SBT Toán 8 Tập 1
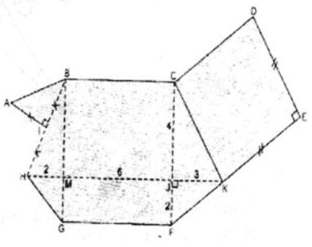
Bạn Giang đã vẽ một đa giác ABCDEFGHI như ở hình bs. 26.
Tính diện tích của đa giác đó, biết rằng : KH song song với BC (K thuộc EF); BC song song với GF; CF song song với BG; BG vuông góc với GF; CK song song với DE; CD song song với FE; KE = DE và KE vuông góc với DE; I là trung điểm của BH, AI = IH và AI vuông góc với IH; HK = 11cm, CF = 6cm. HK cắt CF tại J và JK = 3 (cm), JF = 2cm. BG cắt HK tại M và HM = 2cm.






Thảo luận về Bài viết