Bài tập SGK Bài 2: Tỷ số lượng giác của góc nhọn

Bài tập 10 trang 76 SGK Toán 9 Tập 1

Vẽ một tam giác vuông có một góc nhọn 34⁰ rồi viết các tỉ số lượng giác của góc 340

Bài tập 11 trang 76 SGK Toán 9 Tập 1

Cho tam giác ABC vuông tại C, trong đó $AC=0,9m$, $BC=1,2m$. Tính các tỷ số lượng giác của góc B, từ đó suy ra các tỷ số lượng giác của góc A.

Bài tập 12 trang 76 SGK Toán 9 Tập 1

Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45⁰: $sin{60}^{\circ },cos{75}^{\circ },sin{52}^{\circ }{30}^{\prime },cotg{82}^{\circ },tg{80}^{\circ }.$

Bài tập 13 trang 77 SGK Toán 9 Tập 1

Dựng góc nhọn $\alpha$ , biết:

a) $sin\alpha =\frac{2}{3}$

b) $cos\alpha =0,6$

c) $\tan \alpha =\frac{3}{4}$

d) $cotg\alpha =\frac{3}{2}$

Bài tập 14 trang 77 SGK Toán 9 Tập 1

Sử dụng định nghĩa tỉ số các lượng giác của một góc nhọn để chứng minh rằng: Với góc nhọn  tùy ý, ta có:

a) $tg\alpha =\frac{sin\alpha }{cos\alpha }$                                $cotg\alpha =\frac{cos\alpha }{sin\alpha }$                                 $tg\alpha .cotg\alpha =1$

b) $sin{\alpha }^2+\cos {\alpha }^2=1$

Gợi ý: Sử dụng định lý Py-ta-go.

Bài tập 15 trang 77 SGK Toán 9 Tập 1

Cho tam giác ABC vuông tại A. Biết $cosB=0,8$; hãy tính các tỷ số lượng giác của góc C.

Gợi ý: sử dụng bài tập 14.

Bài tập 16 trang 77 SGK Toán 9 Tập 1

Cho tam giác vuông có một góc bằng 60⁰ và cạnh huyền có độ dài bằng 8. Hãy tìm độ dài của cạnh đối diện góc 600.

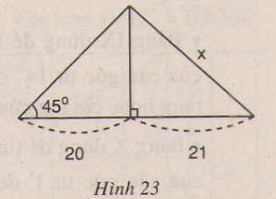
Bài tập 17 trang 77 SGK Toán 9 Tập 1

Tìm giá trị của x trong hình 23:

Bài tập 22 trang 106 SBT Toán 9 Tập 1

Cho tam giác ABC vuông tại A. Chứng minh rằng $\frac{AB}{AC}=\frac{\sin \hat{B}}{\sin \hat{C}}$

Bài tập 24 trang 106 SBT Toán 9 Tập 1

Cho tam giác ABC vuông tại A, AB = 6cm, góc B = α

Biết tg α = 5/12 . Hãy tính:

a. Cạnh AC     

b. Cạnh BC

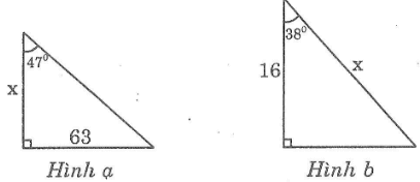
Bài tập 25 trang 107 SBT Toán 9 Tập 1

Tìm giá trị của x (làm tròn đến chữ số thập phân thứ ba) trong mỗi tam giác vuông với kích thước được chỉ ra trên hình sau, biết:

tg47⁰ ≈ 1,072, cos38⁰ ≈ 0,788

Bài tập 26 trang 107 SBT Toán 9 Tập 1

Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.