Câu hỏi Trắc nghiệm (40 câu):
-
Câu 1:
Mã câu hỏi: 84199
Yếu tố nào sau đây xác định một mặt phẳng duy nhất?
- A.Ba điểm
- B.Một điểm và một đường thẳng
- C.Hai đường thẳng cắt nhau
- D.Bốn điểm
-
Câu 2:
Mã câu hỏi: 84200
Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của (SAB) và (SCD) là:
- A.Đường thẳng qua S và song song với AD.
- B.Đường thẳng qua Svà song song với CD.
- C.Đường SO với O là tâm hình bình hành.
- D.Đường thẳng qua S và cắt AB.
-
Câu 3:
Mã câu hỏi: 84201
Cho hình chóp S.ABCD có đáy ABCD là hình thang có đáy lớn AB. Gọi M là trung điểm của SC. Giao điểm của BC với mặt phẳng (ADM) là:
- A.Giao điểm của BC và AM
- B.Giao điểm của BC và SD
- C.Giao điểm của BC và AD
- D.Giao điểm của BC và DM
-
Câu 4:
Mã câu hỏi: 84202
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của AD và BC. Giao tuyến của (SMN) và (SAC) là:
- A.SD
- B.SO (O là trọng tậm của ABCD).
- C.SF (F là trung điểm CD).
- D.SG (F là trung điểm AB).
-
Câu 5:
Mã câu hỏi: 84203
Gọi \(n\) là số cạnh của hình chóp có 101 đỉnh. Tìm \(n\).
- A.\(n = 202\)
- B.\(n = 200\)
- C.\(n = 101\)
- D.\(n = 203\)
-
Câu 6:
Mã câu hỏi: 84204
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của AD và BC. Giao tuyến của (SMN) và (SAC) là:
- A.SD
- B.SO (O là tâm của ABCD).
- C.SF (F là trung điểm CD).
- D.SG (G là trung điểm AB).
-
Câu 7:
Mã câu hỏi: 84205
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC). Khẳng định nào sau đây là khẳng định đúng?
- A.d qua S và song song với BD
- B.d qua S và song song với BC.
- C.d qua S và song song với AB
- D.d qua S và song song với DC.
-
Câu 8:
Mã câu hỏi: 84206
Cho hình tứ diện ABCD có M, N lần lượt là trung điểm của AB, BD Các điểm G, H lần lượt trên cạnh AC, CD sao cho NH cắt MG tại I. Khẳng định nào sau đây là khẳng định đúng?
- A.A, C, I thẳng hàng.
- B.B, C, I thẳng hàng
- C.N, G, H thẳng hàng
- D.B, G, H thẳng hàng
-
Câu 9:
Mã câu hỏi: 84207
Cho hình chóp S.ABCD với đáy là tứ giác lồi có các cạnh đối không song song. AC cắt BD tại O, AD cắt BC tại I. Khi đó, giao tuyến của hai mặt phẳng (SAC) và (SBD) là:
- A.SI
- B.ÍB
- C.SC
- D.SO
-
Câu 10:
Mã câu hỏi: 84208
Cho hình tứ diện ABCD. Gọi M. N lần lượt là trung điểm của AB vàÂC. Gọi d là giao tuyến của (DMN) và mặt phẳng (DBC). Chọn mệnh đề đúng.
- A.\(d // (ABC)\)
- B.\(d \subset \left( {ABC} \right)\)
- C.d cắt (ABC)
- D.\(d // AB\)
-
Câu 11:
Mã câu hỏi: 84209
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA, SB. Giao tuyến của (MNC) và (ABD) là:
- A.OM
- B.CD
- C.OA
- D.ON
-
Câu 12:
Mã câu hỏi: 84210
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AD, BC. Gọi G là trọng tâm \(\Delta BCD.\) Khi đó, giao điểm của đường thẳng MG và mặt phẳng (ABC) là giao điểm của đường thẳng MG và đường thẳng
- A.BC
- B.AC
- C.AN
- D.AB
-
Câu 13:
Mã câu hỏi: 84211
Cho tứ diện ABCD và M là điểm ở trên cạnh AC. Mặt phẳng \(\left( \alpha \right)\) qua và M song song với AB và CD. Thiết diện của tứ diện cắt bởi \(\left( \alpha \right)\) là:
- A.Hình bình hành
- B.Hình chữ nhật
- C.Hình thang
- D.Hình thoi
-
Câu 14:
Mã câu hỏi: 84212
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, K lần lượt là trung điểm của CD,CB,SA. Thiết diện của hình chóp cắt bởi mặt phẳng (MNK) là một đa giác (H). Hãy chọn khẳng định đúng.
- A.(H) là một hình thang
- B.\(H) là một ngũ giác
- C.(H) là một hình bình hành
- D.(H) là một tam giác
-
Câu 15:
Mã câu hỏi: 84213
Cho hình chóp S.ABCD có đáy ABCD là hình thang có đáy lớn AB. Gọi M là trung điểm của SC. Giao điểm của BC với mp(ADM) là:
- A.Giao điểm của BC và AM.
- B.Giao điểm của BC và SD.
- C.Giao điểm của BC và AD
- D.Giao điểm của BC và DM.
-
Câu 16:
Mã câu hỏi: 84214
Cho hình chóp S.ABCD có đáy là hình bình hành. Lấy M là trung điểm cạnh SD. Gọi I là giao điểm của AM và mp (SBC). Mệnh đề nào sau đây là đúng?
- A.SI song song AC
- B.SI song song AD
- C.SI song song CD
- D.SI cắt CD
-
Câu 17:
Mã câu hỏi: 84215
Cho tứ diện ABCD, M và N lần lượt là trung điểm của AB và BC, P là điểm trên cạnh CD sao cho CP=2PD Mặt phẳng (MNP) cắt AD tại Q. Tính tỷ số \(\frac{{AQ}}{{QD}}\).
- A.\(\frac{1}{2}\)
- B.\(3\)
- C.\(\frac{2}{3}\)
- D.\(2\)
-
Câu 18:
Mã câu hỏi: 84216
Cho tứ diện ABCD Gọi E, F lần lượt là trung điểm của các cạnh AC và BC. Trên mặt phẳng BCD lấy một điểm Mtùy ý (điểm Mcó đánh dấu tròn như hình vẽ). Nêu đầy đủ các trường hợp (TH) để thiết diện tạo bởi mặt phẳng (MEF) với tứ diện ABCD là một tứ giác?
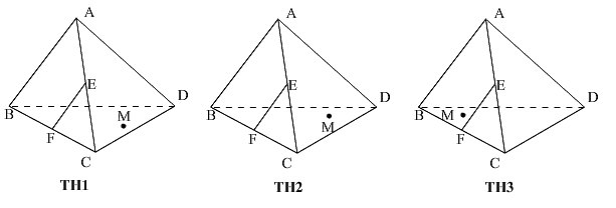
- A.TH1
- B.TH1, TH2
- C.TH2, TH3
- D.TH2
-
Câu 19:
Mã câu hỏi: 84217
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD, E là trung điểm của cạnh SA, F, G là các điểm thuộc cạnh SC, AB (F không là trung điểm của SC). Thiết diện của hình chóp cắt bởi mặt phẳng (EFG) là
- A.Lục giác
- B.Tứ giác
- C.Ngũ giác
- D.Tam giác
-
Câu 20:
Mã câu hỏi: 84218
Trong các phát biểu sau, phát biểu nào đúng?
- A.Hai đường thẳng không có điểm chung thì song song với nhau.
- B.Hai đường thẳng không có điểm chung thì chéo nhau.
- C.Hai đường thẳng phân biệt không cắt nhau thì song song.
- D.Hai đường thẳng không cùng nằm trên một mặt phẳng thì chéo nhau.
-
Câu 21:
Mã câu hỏi: 84219
Cho hai đường thẳng phân biệt \(a, b\) và mặt phẳng \(\left( \alpha \right)\). Giả sử \(a//\left( \alpha \right)\) và \(b//\left( \alpha \right).\) Mệnh đề nào sau đây đúng?
- A.\(a\) và \(b\) chéo nhau
- B.\(a\) và \(b\) hoặc song song hoặc chéo nhau hoặc cắt nhau.
- C.\(a\) và \(b\) hoặc song song hoặc chéo nhau.
- D.\(a\) và \(b\) không có điểm chung
-
Câu 22:
Mã câu hỏi: 84220
Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn là AD. Gọi M là trung điểm của SA, N là giao điểm của cạnh SB và mặt phẳng (MCD). Mệnh đề nào sau đây đúng?
- A.MN và SD cắt nhau
- B.MN và CD cắt nhau
- C.MN và CD song song nhau
- D.MN và SC cắt nhau
-
Câu 23:
Mã câu hỏi: 84221
Cho tứ diện ABCD, gọi I, J, K lần lượt là trung điểm của AC, BC, BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là:
- A.Đường thẳng qua J song song với AC.
- B.Đường thẳng qua J song song với CD.
- C.Đường thẳng qua K song song với AB.
- D.Đường thẳng qua I song song với AD.
-
Câu 24:
Mã câu hỏi: 84222
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng:
- A.GE và CD chéo nhau
- B.GE // CD
- C.GE cắt AD
- D.GE cắt CD
-
Câu 25:
Mã câu hỏi: 84223
Cho hình chóp S.ABCD có đáy ABCDlà hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC). Khẳng định nào sau đây đúng?
- A.d qua S và song song với AB
- B.d qua S và song song với BC
- C.d qua S và song song với BD
- D.d qua S và song song với DC
-
Câu 26:
Mã câu hỏi: 84224
Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm \(\Delta ABD,{\rm{ }}\Delta ABC.\) Tìm mệnh đề đúng
- A.Hai đường thẳng IJ, CD chéo nhau
- B.Đường thẳng IJ cắt CD
- C.Đường thẳng IJ cắt mặt phẳng (BCD).
- D.Đường thẳng IJ // CD
-
Câu 27:
Mã câu hỏi: 84225
Cho hình chóp SABCD có đáy ABCD là một tứ giác (AB không song song CD). Gọi M là trung điểm của SD, N là điểm nằm trên cạnh SB, O là giao điểm của AC và BD. Cặp đường thẳng nào sau đây cắt nhau
- A.SO và AD
- B.MN và SC
- C.SA và BC
- D.MN và SO
-
Câu 28:
Mã câu hỏi: 84226
Cho lăng trụ ABC. A'B'C'. Gọi M, N lần lượt là trung điểm của A 'B' và CC'. Khi đó CB' song song với
- A.AM
- B.A'N
- C.(BC'M)
- D.(AC'M)
-
Câu 29:
Mã câu hỏi: 84227
Cho hình chóp S.ABCD có đáy ABCD là hình thang \(AD//BC,AD = 3BC.\,\,\,M,N\), lần lượt là trung điểm \(AB,CD.\,\,\,G\) là trọng tâm. Mặt phẳng (GMN) cắt hình chóp S.ABCD theo thiết diện là
- A.Hình bình hành
- B.\(\Delta GMN\)
- C.\(\Delta SMN\)
- D.Ngũ giác
-
Câu 30:
Mã câu hỏi: 84228
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB // CD. Gọi M, N lần lượt là trung điểm của SA, BC. Trong các kết luận sau, kết luận nào đúng ?
- A.\(MN//AD\)
- B.\(MN//SB\)
- C.\(MN//(SCD)\)
- D.\(MN//(SBD)\)
-
Câu 31:
Mã câu hỏi: 84229
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là điểm thuộc cạnh BC sao cho MB = 2 MC. Mệnh đề nào sau đây đúng:
- A.\(MG\,{\rm{//}}\,\left( {BCD} \right).\)
- B.\(MG\,{\rm{//}}\,\left( {ACD} \right).\)
- C.\(MG\,{\rm{//}}\,\left( {ABD} \right).\)
- D.\(MG\,{\rm{//}}\,\left( {ABC} \right).\)
-
Câu 32:
Mã câu hỏi: 84230
Cho hình chóp SABCD có đáy ABCD là hình bình hành tâm O, gọi I là trung điểm của cạnh SC. Mệnh đề nào sau đây sai?
- A.IO // (SAB)
- B.IO // (SAD)
- C.Mặt phẳng (IBD) cắt hình chóp SABCD theo thiết diện là một tứ giác.
- D.\(\left( {IBD} \right) \cap \left( {SAD} \right) = IO\)
-
Câu 33:
Mã câu hỏi: 84231
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là điểm thuộc cạnh BC sao cho MB = 2MC. Mệnh đề nào sau đây đúng?
- A.MG // (BCD)
- B.MG // (ACD)
- C.MG // (ABD)
- D.MG // (ABC)
-
Câu 34:
Mã câu hỏi: 84232
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi I là trung điểm SC. Mệnh đề nào sau đây là sai?
- A.\(IO{\rm{//}}(SAB)\)
- B.\((IBD) \cap (SAC) = IO\)
- C.\(IO{\rm{//}}(SAD)\)
- D.(IBD) cắt S.ABCD theo thiết diện là tứ giác
-
Câu 35:
Mã câu hỏi: 84233
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt trung điểm của SA, SB. Giao tuyến của (MNC) và (ABD) là:
- A.OM
- B.CD
- C.OA
- D.ON
-
Câu 36:
Mã câu hỏi: 84234
Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu cặp mặt phẳng song song với nhau lần lượt chứa a và b ?
- A.Vô số
- B.Không có cặp mặt phẳng nào.
- C.2
- D.1
-
Câu 37:
Mã câu hỏi: 84235
Cho hình chóp S.ABCD có đáy là hình bình hành. Hỏi có tất cả bao nhiêu mặt phẳng cách đều 5 điểm S, A, B, C, D ?
- A.2 mặt phẳng
- B.5 mặt phẳng
- C.1 mặt phẳng
- D.4 mặt phẳng
-
Câu 38:
Mã câu hỏi: 84236
CHo hình bình hành ABCD và 1 điểm S không nằm trong mặt phẳng (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là một đường thẳng song song với đường nào sau đây?
- A.AB
- B.AC
- C.BC
- D.SA
-
Câu 39:
Mã câu hỏi: 84237
Hình lăng trụ ABCD. A'B'C'D' gọi là hình hộp nếu đáy ABCD là:
- A.Hình thang
- B.Tứ giác lồi
- C.Hình bình hành
- D.Hình thang cân
-
Câu 40:
Mã câu hỏi: 84238
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi A', B', C', D' lần lượt là trung điểm SA, SB, SC, SD. Trong các trường hợp nào không song song với A'B'?
- A.AB
- B.CD
- C.C'D'
- D.SC
