Bài kiểm tra
Đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Huỳnh Thúc Kháng
1/50
90 : 00
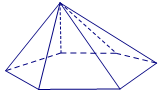
Câu 1: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a và cạnh bên bằng 3a. Một hình nón có đỉnh S và đáy là hình tròn ngoại tiếp hình vuông ABCD. Diện tích xung quanh của hình nón bằng
Câu 2: Tích phân \(\int\limits_{1}^{8}{\sqrt[3]{x}\text{ d}x}\) bằng
Câu 3: Bất phương trình \({{2}^{{{x}^{2}}-3x+4}}\le {{\left( \frac{1}{2} \right)}^{2x-10}}\) có bao nhiêu nghiệm nguyên dương ?
Câu 4: Cho khối hộp \(ABCD.{A}'{B}'{C}'{D}'\) có thể tích bằng \({{a}^{3}}.\) Biết tam giác \({A}'BD\) có diện tích bằng \({{a}^{2}},\) khoảng cách từ điểm A đến mặt phẳng \(\left( {B}'{D}'C \right)\) bằng
Câu 5: Hàm số nào dưới đây đồng biến trên tập \(\mathbb{R}\) ?
Câu 6: Cho hàm số \(y=f\left( x \right).\) Đồ thị của hàm số \(y={f}'\left( x \right)\) như hình bên. Đặt \(g\left( x \right)={{x}^{3}}-3f\left( x \right).\)
Mệnh đề nào dưới đây đúng?
Câu 7: Một hình cầu có bán kính bằng \(\sqrt{3}.\) Thể tích của hình cầu bằng
Câu 8: Trong không gian Oxyz, cho điểm \(M\left( -3;2;5 \right).\) Tìm tọa độ điểm \({M}'\) là hình chiếu vuông góc của điểm M trên trục Ox.
Câu 9: Điểm \(M\) trong hình vẽ bên biểu diễn cho số phức
.PNG)
Câu 10: Gọi \({{z}_{1}},{{z}_{2}}\) là hai nghiệm của phương trình \({{z}^{2}}+z+1=0.\) Tính \(P=z_{1}^{2020}+z_{2}^{2020}.\)
Câu 11: Cho số phức \(z=a+bi(a,b\in \mathbb{R})\) thỏa mãn \(2z-5\bar{z}=-9-14i.\)
Tính S=a+b
Câu 12: Cho hàm số \(y=\sqrt{3x-{{x}^{2}}}\). Hàm số trên đồng biến trên khoảng nào ?
Câu 13: Tính giá trị của biểu thức \(A={{\log }_{a}}\frac{1}{{{a}^{2}}}\) với a>0 và \(a\ne 1\)?
Câu 14: Một đề trắc nghiệm gồm 20 câu, mỗi câu có 4 đáp án và chỉ có một đáp án đúng. Bạn Anh làm đúng 12 câu, còn 8 câu bạn Anh đánh hú họa vào đáp án mà Anh cho là đúng. Mỗi câu đúng được 0,5 điểm. Tính xác suất để Anh được 9 điểm ?
Câu 15: Tất cả giá trị của m để phương trình \(mx-\sqrt{x-3}=m+1\) có hai nghiệm thực phân biệt.
Câu 16: Có bao nhiêu tiếp tuyến với đồ thị hàm số \(y = \dfrac{{2x + 3}}{{x - 1}}\), biết tiếp tuyến song song vối đường thẳng \(y = - 5x - 3\)
Câu 17: Trong không gian Oxyz, cho hai điểm \(A\left( 3;-1;2 \right)\) và \(B\left( 5;3;-2 \right).\) Mặt cầu nhận AB làm đường kính có phương trình là
- A. \({\left( {x + 4} \right)^2} + {\left( {y + 1} \right)^2} + {z^2} = 9\,.\)
- B. \({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} + {z^2} = 9\,.\)
- C. \({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} + {z^2} = 36\,.\)
- D. \({\left( {x + 4} \right)^2} + {\left( {y + 1} \right)^2} + {z^2} = 36\,.\)
Câu 18: Khẳng định nào trong các khẳng định sau là sai?
- A. \(\left( {\int {f(x)dx} } \right)' = f(x)\)
- B. \(\int {\left[ {f(x) + g(x)} \right]} dx = \int {f(x)dx} + \int {g(x)dx} \) với f(x),g(x) liên tục trên R
- C. \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\) với \(\alpha \ne - 1\)
- D. \(\int {kf(x)dx} = k\int {f(x)dx} \) với \(k\in \mathbb{R}\)
Câu 19: Cho hàm số \(f\left( x \right)\) có đạo hàm là \({f}'\left( x \right)={{x}^{3}}{{\left( x-1 \right)}^{2}}\left( x+2 \right)\). Khoảng nghịch biến của hàm số là
Câu 20: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a. Biết tam giác SBD là tam giác đều, thể tích khối chóp S.ABCD bằng
Câu 21: class="MsoNormal" style="text-align:justify">Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):3x-z+2=0.\) Vectơ nào dưới đây là vectơ pháp tuyến của \(\left( P \right)?\)
Câu 22: Cho các số thực x,y thỏa mãn \(\sqrt{2x+3}+\sqrt{y+3}=4\). Giá trị nhỏ nhất của \(\sqrt{x+2}+\sqrt{y+9}\) bằng
Câu 23: Cho lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có cạnh đáy bằng 2a; O là trọng tâm tam giác ABC và \({A}'O=\frac{2\sqrt{6}a}{3}.\) Thể tích của khối lăng trụ \(ABC.{A}'{B}'{C}'\) bằng
Câu 24: Biết \({{z}_{0}}\) là nghiệm phức có phần ảo dương của phương trình \({{z}^{2}}+4z+8=0.\) Trên mặt phẳng tọa độ, điểm nào dưới đây biểu diễn số phức \(w={{z}_{0}}.\left( -3+5i \right)?\)
Câu 25: Ông Anh muốn mua một chiếc ô tô trị giá 700 triệu đồng nhưng ông chỉ có 500 triệu đồng và muốn vay ngân hàng 200 triệu đồng theo phương thức trả góp với lãi suất 0,75% tháng. Hỏi hàng tháng ông Anh phải trả số tiền là bao nhiêu để sau đúng hai năm thì trả hết nợ ngân hàng?
Câu 26: Giá trị của biểu thức \(K = \frac{{{2^3}{{.2}^{ - 1}} + {5^{ - 3}}{{.5}^4}}}{{{{10}^{ - 3}}:{{10}^{ - 2}} - {{(0,25)}^0}}}\) là
Câu 27: Cho \(F\left( x \right)=\frac{-1}{2{{\sin }^{2}}x}\) là một nguyên hàm của hàm số \(\frac{f\left( x \right)}{{{\cos }^{2}}x}.\) Tìm họ nguyên hàm của hàm số \({f}'\left( x \right)\tan x.\)
- A. \(\int {f'\left( x \right)\tan x{\rm{d}}x} = \frac{{\cos x}}{{{{\sin }^3}x}} - \frac{1}{{2{{\sin }^2}x}} + C.\)
- B. \(\int {f'\left( x \right)\tan x{\rm{d}}x} = \frac{3}{2}{\cot ^2}x + C.\)
- C. \(\int {f'\left( x \right)\tan x{\rm{d}}x} = \frac{1}{2}{\cot ^2}x + C.\)
- D. \(\int {f'\left( x \right)\tan x{\rm{d}}x} = \frac{{\cos x}}{{{{\sin }^3}x}} + \frac{1}{{2{{\sin }^2}x}} + C.\)
Câu 28: Cho hàm số \(y=\frac{x+1}{x-1}\) có đồ thị là (C). Gọi \(M\left( {{x}_{M}};{{y}_{M}} \right)\) là một điểm bất kỳ trên (C). Khi tổng khoảng cách từ M đến hai trục tọa độ là nhỏ nhất, tính tổng \({{x}_{M}}+{{y}_{M}}\).
Câu 29: Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên \(\left( -\infty ;0 \right)\) và \(\left( 0;+\infty \right)\) có bảng biến thiên như hình bên.
Mệnh đề nào sau đây đúng ?
Câu 30: Trong không gian Oxyz, cho hai mặt phẳng \(\left( P \right)\) và \(\left( {{P}'} \right)\) lần lượt có phương trình x+2y-2z+1=0 và x-2y+2z-1=0. Gọi \(\left( S \right)\) là tập hợp các điểm cách đều hai mặt phẳng \(\left( P \right)\) và \(\left( {{P}'} \right).\) Mệnh đề nào dưới đây đúng ?
Câu 31: Trong không gian với hệ tọa độ Oxyz, xét mặt cầu có phương trình \({{x}^{2}}-2ax+{{y}^{2}}-2by+{{\left( z-c \right)}^{2}}=0,\) với a,b,c là các tham số và a,b không đồng thời bằng 0. Mệnh đề nào dưới đây đúng ?
Câu 32: Cho hàm số y=f(x) có đạo hàm trên \(\left( a;b \right)\). Phát biểu nào sau đây là đúng ?
- A. Hàm số y=f(x) không đổi khi và chỉ khi \({f}'(x)<0,\forall x\in \left( a;b \right)\).
- B. Hàm số y=f(x) đồng biến khi và chỉ khi \({f}'(x)\ge 0,\forall x\in \left( a;b \right)\) và f'(x)=0 tại hữu hạn giá trị \(x\in \left( a;b \right).\)
- C. Hàm số y=f(x) nghịch biến khi và chỉ khi \({f}'(x)\le 0,\forall x\in \left( a;b \right)\).
- D. Hàm số y=f(x) đồng biến khi và chỉ khi \({f}'(x)\ge 0,\forall x\in \left( a;b \right)\)
Câu 33: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=-\frac{{{x}^{3}}}{3}+m{{x}^{2}}+2\) nghịch biến trên \(\mathbb{R}\)
Câu 35: Cho tích phân \(I=\int\limits_{0}^{\pi }{{{x}^{2}}\cos x\text{d}x}\) và \(u={{x}^{2}},\text{d}v=\cos x\,\text{d}x\). Khẳng định nào sau đây đúng ?
- A. \(I = {x^2}\sin x\left| {_0^\pi } \right. + \int\limits_0^\pi {x\sin x{\rm{d}}x} \)
- B. \(I = {x^2}\sin x\left| {_0^\pi } \right. + 2\int\limits_0^\pi {x\sin x{\rm{d}}x} \)
- C. \(I = {x^2}\sin x\left| {_0^\pi } \right. - 2\int\limits_0^\pi {x\sin x{\rm{d}}x} \)
- D. \(I = {x^2}\sin x\left| {_0^\pi } \right. - \int\limits_0^\pi {x\sin x{\rm{d}}x} \)
Câu 36: Cho \({{z}_{1}}=2m+\left( m-2 \right)i\) và \({{z}_{2}}=3-4mi,\) với m là số thực. Biết \({{z}_{1}}.{{z}_{2}}\) là số thuần ảo. Mệnh đề nào dưới đây đúng ?
Câu 37: Cho biết ba số khác không a, b, c theo thứ tự lập thành cấp số nhân. Mệnh đề nào dưới đây đúng ?
Câu 38: Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ 0;\frac{\pi }{4} \right]\) thỏa mãn \(f\left( 0 \right)=0, \int\limits_{\text{0}}^{\frac{\pi }{\text{4}}}{{{\left[ {f}'\left( x \right) \right]}^{2}}\text{d}x}=2\) và \(\int\limits_{\text{0}}^{\frac{\pi }{\text{4}}}{\sin 2x.f\left( x \right)\text{d}x}=\frac{1}{2}.\) Tích phân \(\int\limits_{\text{0}}^{\frac{\pi }{\text{4}}}{f\left( x \right)\text{d}x}\) bằng
Câu 39: Trong không gian Oxyz, cho đường thẳng \(d:\left\{ \begin{array}{l} x = 1\\ y = 2 + 3t\\ z = 5 - t \end{array} \right.(t \in R).\) Vectơ nào dưới đây là vectơ chỉ phương của d?
Câu 40: Hàm số \(y=\frac{2x-1}{x-2}\) nghịch biến trên khoảng nào ?
Câu 41: Nếu \({{\left( 7+4\sqrt{3} \right)}^{a-1}}<7-4\sqrt{3}\) thì
Câu 42: Trong không gian Oxyz, cho \(\vec{a}=\left( 1;1;-2 \right)\) và \(\vec{b}=\left( -2;1;1 \right).\) Gọi \(\alpha \) là góc giữa hai vectơ \(\vec{a}\) và \(\vec{b}.\) Khẳng định nào dưới đây đúng ?
Câu 43: Tìm tập xác định D của hàm số \(y={{\log }_{3}}\left( {{x}^{2}}-4x+3 \right)\).
Câu 44: Tìm m để phương trình \(\cos 2x+2(m+1)\sin x-2m-1=0\) có đúng 3 nghiệm \(x\in \left( 0;\pi \right).\)
Câu 45: Hàm số \(y={{x}^{4}}-2{{x}^{2}}\) đồng biến trên khoảng
Câu 46: Một hộp chứa 7 viên bi khác nhau. Lấy ngẫu nhiên 2 viên bi trong hộp. Số cách lấy là
Câu 47: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SD=\frac{3a}{2}\). Hình chiếu vuông góc của điểm S lên mặt phẳng đáy là trung điểm của cạnh AB. Tính khoảng cách từ điểm A đến mặt phẳng \(\left( SBD \right)\).
Câu 48: Xét các số nguyên dương a,b sao cho phương trình \(b{{\ln }^{2}}x+a\ln x+3=0\) có hai nghiệm phân biệt \({{x}_{1}},{{x}_{2}}\) và phương trình \(3{{\log }^{2}}x+a\log x+b=0\) có hai nghiệm phân biệt \({{x}_{3}},{{x}_{4}}\) thỏa mãn \(\ln {{\left( {{x}_{1}}{{x}_{2}} \right)}^{10}}>\log {{\left( {{x}_{3}}{{x}_{4}} \right)}^{e}}.\) Tính giá trị nhỏ nhất \({{S}_{\min }}\) của S=5a+3b.
Câu 49: Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có cạnh đáy bằng a và cạnh bên bằng 2a. Một hình trụ có hai đáy là hai hình tròn ngoại tiếp hai tam giác ABC và \({A}'{B}'{C}'.\) Diện tích xung quanh của hình trụ bằng
Câu 50: Trong không gian Oxyz, cho hai điểm \(A\left( 1;2;1 \right)\) và \(B\left( 4;5;-2 \right).\) Đường thẳng AB cắt mặt phẳng \(\left( P \right):3x-4y+5z+6=0\) tại điểm M. Tính tỉ số \(\frac{BM}{AM}.\)


.PNG)
.PNG)