Câu hỏi Trắc nghiệm (50 câu):
-
Câu 1:
Mã câu hỏi: 110388
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a và cạnh bên bằng 3a. Một hình nón có đỉnh S và đáy là hình tròn ngoại tiếp hình vuông ABCD. Diện tích xung quanh của hình nón bằng
- A.\(3\sqrt 2 \pi {a^2}.\)
- B.\(\frac{{3\sqrt 2 \pi {a^2}}}{2}.\)
- C.\(6\pi {a^2}.\)
- D.\(6\sqrt 2 \pi {a^2}.\)
-
Câu 2:
Mã câu hỏi: 110389
Tích phân \(\int\limits_{1}^{8}{\sqrt[3]{x}\text{ d}x}\) bằng
- A.2
- B.\(\frac{{45}}{4}\)
- C.\(\frac{{47}}{4}\)
- D.\(\frac{{25}}{4}\)
-
Câu 3:
Mã câu hỏi: 110390
Bất phương trình \({{2}^{{{x}^{2}}-3x+4}}\le {{\left( \frac{1}{2} \right)}^{2x-10}}\) có bao nhiêu nghiệm nguyên dương ?
- A.2
- B.3
- C.6
- D.3
-
Câu 4:
Mã câu hỏi: 110391
Cho khối hộp \(ABCD.{A}'{B}'{C}'{D}'\) có thể tích bằng \({{a}^{3}}.\) Biết tam giác \({A}'BD\) có diện tích bằng \({{a}^{2}},\) khoảng cách từ điểm A đến mặt phẳng \(\left( {B}'{D}'C \right)\) bằng
- A.3a
- B.\(\frac{a}{2}.\)
- C.a
- D.2a
-
Câu 5:
Mã câu hỏi: 110392
Hàm số nào dưới đây đồng biến trên tập \(\mathbb{R}\) ?
- A.y = 2x - 1
- B.\(y = - {x^2} + 1\)
- C.\(y = {x^2} + 1\)
- D.y = - 2x + 1.
-
Câu 6:
Mã câu hỏi: 110393
Cho hàm số \(y=f\left( x \right).\) Đồ thị của hàm số \(y={f}'\left( x \right)\) như hình bên. Đặt \(g\left( x \right)={{x}^{3}}-3f\left( x \right).\)
.PNG)
Mệnh đề nào dưới đây đúng?
- A.\(g\left( 0 \right) < g\left( { - 1} \right) < g\left( 2 \right).\)
- B.\(g\left( 2 \right) < g\left( { - 1} \right) < g\left( 0 \right).\)
- C.\(g\left( 2 \right) < g\left( 0 \right) < g\left( { - 1} \right).\)
- D.\(g\left( { - 1} \right) < g\left( 0 \right) < g\left( 2 \right).\)
-
Câu 7:
Mã câu hỏi: 110394
Một hình cầu có bán kính bằng \(\sqrt{3}.\) Thể tích của hình cầu bằng
- A.\(\sqrt 3 \pi .\)
- B.\(12\pi .\)
- C.\(3\pi .\)
- D.\(4\sqrt 3 \pi .\)
-
Câu 8:
Mã câu hỏi: 110395
Trong không gian Oxyz, cho điểm \(M\left( -3;2;5 \right).\) Tìm tọa độ điểm \({M}'\) là hình chiếu vuông góc của điểm M trên trục Ox.
- A.\(M'\left( {3; - 2; - 5} \right).\)
- B.\(M'\left( { - 3;0;0} \right).\)
- C.\(M'\left( {0;2;0} \right).\)
- D.\(M'\left( {0;0;5} \right).\)
-
Câu 9:
Mã câu hỏi: 110396
Điểm \(M\) trong hình vẽ bên biểu diễn cho số phức
.PNG)
- A.2 - 3i.
- B.- 3 + 2i.
- C.2 + 3i.
- D.- 3 - 2i.
-
Câu 10:
Mã câu hỏi: 110397
Gọi \({{z}_{1}},{{z}_{2}}\) là hai nghiệm của phương trình \({{z}^{2}}+z+1=0.\) Tính \(P=z_{1}^{2020}+z_{2}^{2020}.\)
- A.P = 1
- B.P = -1
- C.P = 0
- D.P = 2
-
Câu 11:
Mã câu hỏi: 110398
Cho số phức \(z=a+bi(a,b\in \mathbb{R})\) thỏa mãn \(2z-5\bar{z}=-9-14i.\)
Tính S=a+b
- A.S = -1
- B.S = 1
- C.\(S = - \frac{{23}}{3}.\)
- D.\(S = \frac{{23}}{3}.\)
-
Câu 12:
Mã câu hỏi: 110399
Cho hàm số \(y=\sqrt{3x-{{x}^{2}}}\). Hàm số trên đồng biến trên khoảng nào ?
- A.\(\left( {\frac{3}{2};3} \right)\)
- B.(0;2)
- C.\(\left( {0;\frac{3}{2}} \right)\)
- D.(0;3)
-
Câu 13:
Mã câu hỏi: 110400
Tính giá trị của biểu thức \(A={{\log }_{a}}\frac{1}{{{a}^{2}}}\) với a>0 và \(a\ne 1\)?
- A.\(A = \frac{1}{2}\)
- B.A = 2
- C.A = -2
- D.\(A = - \frac{1}{2}\)
-
Câu 14:
Mã câu hỏi: 110401
Một đề trắc nghiệm gồm 20 câu, mỗi câu có 4 đáp án và chỉ có một đáp án đúng. Bạn Anh làm đúng 12 câu, còn 8 câu bạn Anh đánh hú họa vào đáp án mà Anh cho là đúng. Mỗi câu đúng được 0,5 điểm. Tính xác suất để Anh được 9 điểm ?
- A.\(\frac{{63}}{{16384}}\)
- B.\(\frac{9}{{10}}\)
- C.\(\frac{9}{{65536}}\)
- D.\(\frac{9}{{20}}\)
-
Câu 15:
Mã câu hỏi: 110402
Tất cả giá trị của m để phương trình \(mx-\sqrt{x-3}=m+1\) có hai nghiệm thực phân biệt.
- A.m > 0
- B.\(\frac{1}{2} \le m \le \frac{{\sqrt 3 }}{2}\)
- C.\(\frac{1}{2} \le m < \frac{{1 + \sqrt 3 }}{4}\)
- D.\(0 < m < \frac{{1 + \sqrt 3 }}{4}\)
-
Câu 16:
Mã câu hỏi: 110403
Có bao nhiêu tiếp tuyến với đồ thị hàm số \(y = \dfrac{{2x + 3}}{{x - 1}}\), biết tiếp tuyến song song vối đường thẳng \(y = - 5x - 3\)
- A.1
- B.0
- C.2
- D.3
-
Câu 17:
Mã câu hỏi: 110404
Trong không gian Oxyz, cho hai điểm \(A\left( 3;-1;2 \right)\) và \(B\left( 5;3;-2 \right).\) Mặt cầu nhận AB làm đường kính có phương trình là
- A.\({\left( {x + 4} \right)^2} + {\left( {y + 1} \right)^2} + {z^2} = 9\,.\)
- B.\({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} + {z^2} = 9\,.\)
- C.\({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} + {z^2} = 36\,.\)
- D.\({\left( {x + 4} \right)^2} + {\left( {y + 1} \right)^2} + {z^2} = 36\,.\)
-
Câu 18:
Mã câu hỏi: 110405
Khẳng định nào trong các khẳng định sau là sai?
- A.\(\left( {\int {f(x)dx} } \right)' = f(x)\)
- B.\(\int {\left[ {f(x) + g(x)} \right]} dx = \int {f(x)dx} + \int {g(x)dx} \) với f(x),g(x) liên tục trên R
- C.\(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\) với \(\alpha \ne - 1\)
- D.\(\int {kf(x)dx} = k\int {f(x)dx} \) với \(k\in \mathbb{R}\)
-
Câu 19:
Mã câu hỏi: 110406
Cho hàm số \(f\left( x \right)\) có đạo hàm là \({f}'\left( x \right)={{x}^{3}}{{\left( x-1 \right)}^{2}}\left( x+2 \right)\). Khoảng nghịch biến của hàm số là
- A.\(\left( { - \infty ; - 2} \right);\,\left( {0; + \infty } \right)\)
- B.\(\left( { - 2;0} \right)\)
- C.\(\left( { - \infty ; - 2} \right);\,\left( {0;1} \right)\)
- D.\(\left( { - 2;0} \right);\,\left( {1; + \infty } \right)\)
-
Câu 20:
Mã câu hỏi: 110407
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a. Biết tam giác SBD là tam giác đều, thể tích khối chóp S.ABCD bằng
- A.\(\frac{{9{a^3}}}{2}.\)
- B.\(\frac{{243\sqrt 3 {a^3}}}{4}.\)
- C.9a3
- D.\({\rm{9}}\sqrt {\rm{3}} {a^3}.\)
-
Câu 21:
Mã câu hỏi: 110408
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):3x-z+2=0.\) Vectơ nào dưới đây là vectơ pháp tuyến của \(\left( P \right)?\)
- A.\({\vec n_4} = \left( {3;0; - 1} \right).\)
- B.\({\vec n_2} = \left( {3; - 1;2} \right).\)
- C.\({\vec n_3} = \left( {3; - 1;0} \right).\)
- D.\({\vec n_1} = \left( { - 1;0; - 1} \right).\)
-
Câu 22:
Mã câu hỏi: 110409
Cho các số thực x,y thỏa mãn \(\sqrt{2x+3}+\sqrt{y+3}=4\). Giá trị nhỏ nhất của \(\sqrt{x+2}+\sqrt{y+9}\) bằng
- A.\(\sqrt 6 + \sqrt {\frac{{17}}{2}} \)
- B.\(\sqrt 3 \)
- C.\(\frac{{3\sqrt {10} }}{2}\)
- D.\(\sqrt {\frac{1}{2}} + \sqrt {21} \)
-
Câu 23:
Mã câu hỏi: 110410
Cho lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có cạnh đáy bằng 2a; O là trọng tâm tam giác ABC và \({A}'O=\frac{2\sqrt{6}a}{3}.\) Thể tích của khối lăng trụ \(ABC.{A}'{B}'{C}'\) bằng
- A.2a3
- B.\(\frac{{4{a^3}}}{3}.\)
- C.\(\frac{{2{a^3}}}{3}.\)
- D.4a3
-
Câu 24:
Mã câu hỏi: 110411
Biết \({{z}_{0}}\) là nghiệm phức có phần ảo dương của phương trình \({{z}^{2}}+4z+8=0.\) Trên mặt phẳng tọa độ, điểm nào dưới đây biểu diễn số phức \(w={{z}_{0}}.\left( -3+5i \right)?\)
- A.P(-4;-16)
- B.M(-2;2)
- C.N(16;4)
- D.Q(16;-4)
-
Câu 25:
Mã câu hỏi: 110412
Ông Anh muốn mua một chiếc ô tô trị giá 700 triệu đồng nhưng ông chỉ có 500 triệu đồng và muốn vay ngân hàng 200 triệu đồng theo phương thức trả góp với lãi suất 0,75% tháng. Hỏi hàng tháng ông Anh phải trả số tiền là bao nhiêu để sau đúng hai năm thì trả hết nợ ngân hàng?
- A.913.5000 đồng
- B.997.0000 đồng
- C.997.1000 đồng
- D.913.7000 đồng
-
Câu 26:
Mã câu hỏi: 110413
Giá trị của biểu thức \(K = \frac{{{2^3}{{.2}^{ - 1}} + {5^{ - 3}}{{.5}^4}}}{{{{10}^{ - 3}}:{{10}^{ - 2}} - {{(0,25)}^0}}}\) là
- A.12
- B.15
- C.-10
- D.10
-
Câu 27:
Mã câu hỏi: 110414
Cho \(F\left( x \right)=\frac{-1}{2{{\sin }^{2}}x}\) là một nguyên hàm của hàm số \(\frac{f\left( x \right)}{{{\cos }^{2}}x}.\) Tìm họ nguyên hàm của hàm số \({f}'\left( x \right)\tan x.\)
- A.\(\int {f'\left( x \right)\tan x{\rm{d}}x} = \frac{{\cos x}}{{{{\sin }^3}x}} - \frac{1}{{2{{\sin }^2}x}} + C.\)
- B.\(\int {f'\left( x \right)\tan x{\rm{d}}x} = \frac{3}{2}{\cot ^2}x + C.\)
- C.\(\int {f'\left( x \right)\tan x{\rm{d}}x} = \frac{1}{2}{\cot ^2}x + C.\)
- D.\(\int {f'\left( x \right)\tan x{\rm{d}}x} = \frac{{\cos x}}{{{{\sin }^3}x}} + \frac{1}{{2{{\sin }^2}x}} + C.\)
-
Câu 28:
Mã câu hỏi: 110415
Cho hàm số \(y=\frac{x+1}{x-1}\) có đồ thị là (C). Gọi \(M\left( {{x}_{M}};{{y}_{M}} \right)\) là một điểm bất kỳ trên (C). Khi tổng khoảng cách từ M đến hai trục tọa độ là nhỏ nhất, tính tổng \({{x}_{M}}+{{y}_{M}}\).
- A.\(2 - \sqrt 2 .\)
- B.\(2\sqrt 2 - 1.\)
- C.1
- D.\(2 - 2\sqrt 2 .\)
-
Câu 29:
Mã câu hỏi: 110416
Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên \(\left( -\infty ;0 \right)\) và \(\left( 0;+\infty \right)\) có bảng biến thiên như hình bên.
.PNG)
Mệnh đề nào sau đây đúng ?
- A.Hàm số có giá trị nhỏ nhất bằng 2
- B.\(f\left( { - 3} \right) > f\left( { - 2} \right)\)
- C.Hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
- D.Đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số
-
Câu 30:
Mã câu hỏi: 110417
Trong không gian Oxyz, cho hai mặt phẳng \(\left( P \right)\) và \(\left( {{P}'} \right)\) lần lượt có phương trình x+2y-2z+1=0 và x-2y+2z-1=0. Gọi \(\left( S \right)\) là tập hợp các điểm cách đều hai mặt phẳng \(\left( P \right)\) và \(\left( {{P}'} \right).\) Mệnh đề nào dưới đây đúng ?
- A.(S) là mặt phẳng có phương trình x = 0
- B.(S) là mặt phẳng có phương trình 2y - 2z + 1 = 0.
- C.\(\left( S \right)\) là đường thẳng xác định bởi giao tuyến của hai mặt phẳng có phương trình x=0 và 2y-2z+1=0.
- D.\(\left( S \right)\) là hai mặt phẳng có phương trình x=0 và 2y-2z+1=0.
-
Câu 31:
Mã câu hỏi: 110418
Trong không gian với hệ tọa độ Oxyz, xét mặt cầu có phương trình \({{x}^{2}}-2ax+{{y}^{2}}-2by+{{\left( z-c \right)}^{2}}=0,\) với a,b,c là các tham số và a,b không đồng thời bằng 0. Mệnh đề nào dưới đây đúng ?
- A.Mọi mặt cầu đó tiếp xúc với mặt phẳng (Oxy)
- B.Mọi mặt cầu đó tiếp xúc với trục Oz
- C.Mọi mặt cầu đó tiếp xúc với các trục Ox và Oy
- D.Mọi mặt cầu đó đi qua gốc tọa độ O
-
Câu 32:
Mã câu hỏi: 110419
Cho hàm số y=f(x) có đạo hàm trên \(\left( a;b \right)\). Phát biểu nào sau đây là đúng ?
- A.Hàm số y=f(x) không đổi khi và chỉ khi \({f}'(x)<0,\forall x\in \left( a;b \right)\).
- B.Hàm số y=f(x) đồng biến khi và chỉ khi \({f}'(x)\ge 0,\forall x\in \left( a;b \right)\) và f'(x)=0 tại hữu hạn giá trị \(x\in \left( a;b \right).\)
- C.Hàm số y=f(x) nghịch biến khi và chỉ khi \({f}'(x)\le 0,\forall x\in \left( a;b \right)\).
- D.Hàm số y=f(x) đồng biến khi và chỉ khi \({f}'(x)\ge 0,\forall x\in \left( a;b \right)\)
-
Câu 33:
Mã câu hỏi: 110420
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=-\frac{{{x}^{3}}}{3}+m{{x}^{2}}+2\) nghịch biến trên \(\mathbb{R}\)
- A.m = 0
- B.\(\left[ \begin{array}{l} m > 1\\ m < 0 \end{array} \right.\)
- C.\(\left[ \begin{array}{l} m \ge 1\\ m \le 0 \end{array} \right.\)
- D.\(0 \le m \le 1\)
-
Câu 34:
Mã câu hỏi: 110421
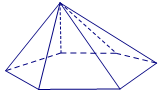
Hình đa diện trong hình vẽ bên có bao nhiêu mặt ?
- A.4
- B.6
- C.5
- D.7
-
Câu 35:
Mã câu hỏi: 110422
Cho tích phân \(I=\int\limits_{0}^{\pi }{{{x}^{2}}\cos x\text{d}x}\) và \(u={{x}^{2}},\text{d}v=\cos x\,\text{d}x\). Khẳng định nào sau đây đúng ?
- A.\(I = {x^2}\sin x\left| {_0^\pi } \right. + \int\limits_0^\pi {x\sin x{\rm{d}}x} \)
- B.\(I = {x^2}\sin x\left| {_0^\pi } \right. + 2\int\limits_0^\pi {x\sin x{\rm{d}}x} \)
- C.\(I = {x^2}\sin x\left| {_0^\pi } \right. - 2\int\limits_0^\pi {x\sin x{\rm{d}}x} \)
- D.\(I = {x^2}\sin x\left| {_0^\pi } \right. - \int\limits_0^\pi {x\sin x{\rm{d}}x} \)
-
Câu 36:
Mã câu hỏi: 110423
Cho \({{z}_{1}}=2m+\left( m-2 \right)i\) và \({{z}_{2}}=3-4mi,\) với m là số thực. Biết \({{z}_{1}}.{{z}_{2}}\) là số thuần ảo. Mệnh đề nào dưới đây đúng ?
- A.\(m \in \left[ {0;2} \right).\)
- B.\(m \in \left[ {2;5} \right].\)
- C.\(m \in \left( { - 3;0} \right).\)
- D.\(m \in \left( { - 5; - 2} \right).\)
-
Câu 37:
Mã câu hỏi: 110424
Cho biết ba số khác không a, b, c theo thứ tự lập thành cấp số nhân. Mệnh đề nào dưới đây đúng ?
- A.\(ac = {b^2}.\)
- B.a + c = 2b.
- C.a + b = 2c.
- D.b + c = 2a.
-
Câu 38:
Mã câu hỏi: 110425
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ 0;\frac{\pi }{4} \right]\) thỏa mãn \(f\left( 0 \right)=0, \int\limits_{\text{0}}^{\frac{\pi }{\text{4}}}{{{\left[ {f}'\left( x \right) \right]}^{2}}\text{d}x}=2\) và \(\int\limits_{\text{0}}^{\frac{\pi }{\text{4}}}{\sin 2x.f\left( x \right)\text{d}x}=\frac{1}{2}.\) Tích phân \(\int\limits_{\text{0}}^{\frac{\pi }{\text{4}}}{f\left( x \right)\text{d}x}\) bằng
- A.\(\frac{{ - 1}}{2}.\)
- B.\(\frac{{ 1}}{2}.\)
- C.\(\frac{{ - 1}}{4}.\)
- D.\(\frac{{ 1}}{4}.\)
-
Câu 39:
Mã câu hỏi: 110426
Trong không gian Oxyz, cho đường thẳng \(d:\left\{ \begin{array}{l} x = 1\\ y = 2 + 3t\\ z = 5 - t \end{array} \right.(t \in R).\) Vectơ nào dưới đây là vectơ chỉ phương của d?
- A.\({\vec u_4} = \left( {1;2;5} \right).\)
- B.\({\vec u_1} = \left( {1;3; - 1} \right).\)
- C.\({\vec u_3} = \left( {1; - 3; - 1} \right).\)
- D.\({\vec u_2} = \left( {0;3; - 1} \right).\)
-
Câu 40:
Mã câu hỏi: 110427
Hàm số \(y=\frac{2x-1}{x-2}\) nghịch biến trên khoảng nào ?
- A.R\{2}
- B.\(\left( { - 2;\, + \infty } \right)\)
- C.\(\left( { 2;\, + \infty } \right)\)
- D.R
-
Câu 41:
Mã câu hỏi: 110428
Nếu \({{\left( 7+4\sqrt{3} \right)}^{a-1}}<7-4\sqrt{3}\) thì
- A.a < 1
- B.a > 1
- C.a > 0
- D.a < 0
-
Câu 42:
Mã câu hỏi: 110429
Trong không gian Oxyz, cho \(\vec{a}=\left( 1;1;-2 \right)\) và \(\vec{b}=\left( -2;1;1 \right).\) Gọi \(\alpha \) là góc giữa hai vectơ \(\vec{a}\) và \(\vec{b}.\) Khẳng định nào dưới đây đúng ?
- A.\(\alpha = {60^0}.\)
- B.\(\alpha = {45^0}.\)
- C.\(\alpha = {120^0}.\)
- D.\(\alpha = {90^0}.\)
-
Câu 43:
Mã câu hỏi: 110430
Tìm tập xác định D của hàm số \(y={{\log }_{3}}\left( {{x}^{2}}-4x+3 \right)\).
- A.\(D = \left( { - \infty ;2 - \sqrt 2 } \right) \cup \left( {2 + \sqrt 2 ; + \infty } \right)\)
- B.\(D = \left( {2 - \sqrt 2 ;1} \right) \cup \left( {3;2 + \sqrt 2 } \right)\)
- C.\(D = \left( {1;3} \right)\)
- D.\(D = \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
-
Câu 44:
Mã câu hỏi: 110431
Tìm m để phương trình \(\cos 2x+2(m+1)\sin x-2m-1=0\) có đúng 3 nghiệm \(x\in \left( 0;\pi \right).\)
- A.\(0 \le m < 1\)
- B.- 1 < m < 1
- C.\(0 < m \le 1\)
- D.0 < m < 1
-
Câu 45:
Mã câu hỏi: 110432
Hàm số \(y={{x}^{4}}-2{{x}^{2}}\) đồng biến trên khoảng
- A.\(\left( { - \infty ;1} \right)\)
- B.\(\left( {0; + \infty } \right)\)
- C.(0;1) và \(\left( {1; + \infty } \right)\)
- D.(-1;0) và \(\left( {1; + \infty } \right)\)
-
Câu 46:
Mã câu hỏi: 110433
Một hộp chứa 7 viên bi khác nhau. Lấy ngẫu nhiên 2 viên bi trong hộp. Số cách lấy là
- A.21
- B.12
- C.42
- D.6
-
Câu 47:
Mã câu hỏi: 110434
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SD=\frac{3a}{2}\). Hình chiếu vuông góc của điểm S lên mặt phẳng đáy là trung điểm của cạnh AB. Tính khoảng cách từ điểm A đến mặt phẳng \(\left( SBD \right)\).
- A.\(d = \frac{{2a}}{3}.\)
- B.\(d = \frac{{3a}}{5}.\)
- C.\(d = \frac{{3a}}{2}.\)
- D.\(d = \frac{{3a}}{4}.\)
-
Câu 48:
Mã câu hỏi: 110435
Xét các số nguyên dương a,b sao cho phương trình \(b{{\ln }^{2}}x+a\ln x+3=0\) có hai nghiệm phân biệt \({{x}_{1}},{{x}_{2}}\) và phương trình \(3{{\log }^{2}}x+a\log x+b=0\) có hai nghiệm phân biệt \({{x}_{3}},{{x}_{4}}\) thỏa mãn \(\ln {{\left( {{x}_{1}}{{x}_{2}} \right)}^{10}}>\log {{\left( {{x}_{3}}{{x}_{4}} \right)}^{e}}.\) Tính giá trị nhỏ nhất \({{S}_{\min }}\) của S=5a+3b.
- A.\({S_{\min }} = 102.\)
- B.\({S_{\min }} = 101.\)
- C.\({S_{\min }} = 96.\)
- D.\({S_{\min }} = 99.\)
-
Câu 49:
Mã câu hỏi: 110436
Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có cạnh đáy bằng a và cạnh bên bằng 2a. Một hình trụ có hai đáy là hai hình tròn ngoại tiếp hai tam giác ABC và \({A}'{B}'{C}'.\) Diện tích xung quanh của hình trụ bằng
- A.\(\frac{{4\sqrt 3 \pi {a^2}}}{3}.\)
- B.\(\frac{{2\sqrt 3 \pi {a^2}}}{3}.\)
- C.\(4\pi {a^2}.\)
- D.\(2\pi {a^2}.\)
-
Câu 50:
Mã câu hỏi: 110437
Trong không gian Oxyz, cho hai điểm \(A\left( 1;2;1 \right)\) và \(B\left( 4;5;-2 \right).\) Đường thẳng AB cắt mặt phẳng \(\left( P \right):3x-4y+5z+6=0\) tại điểm M. Tính tỉ số \(\frac{BM}{AM}.\)
- A.\(\frac{{BM}}{{AM}} = 2.\)
- B.\(\frac{{BM}}{{AM}} = 4.\)
- C.\(\frac{{BM}}{{AM}} = \frac{1}{4}.\)
- D.\(\frac{{BM}}{{AM}} = 3.\)
