Câu hỏi Trắc nghiệm (50 câu):
-
Câu 1:
Mã câu hỏi: 83352
Tính giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{x + 2}}.\)
- A.1
- B.2
- C.3
- D.4
-
Câu 2:
Mã câu hỏi: 83353
Tính giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \frac{{x + \sqrt {{x^2} + 1} }}{{x + 2}}.\)
- A.1
- B.2
- C.3
- D.4
-
Câu 3:
Mã câu hỏi: 83354
Cho \(\mathop {\lim }\limits_{x \to 1} \frac{{x + \sqrt {{x^2} + 1} }}{{x + 1}} = a + b\sqrt 2 (a,b \in Q).\). Tính \(a+b\)
- A.1
- B.2
- C.5
- D.0
-
Câu 4:
Mã câu hỏi: 83355
Tính giới hạn \(\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} + x - 2}}{{x - 1}}.\)
- A.1
- B.- 2
- C.3
- D.5
-
Câu 5:
Mã câu hỏi: 83356
Tính giới hạn \(\mathop {\lim }\limits_{x\,\, \to \,\,2} (x - 2)\)
- A.7
- B.- 2
- C.3
- D.0
-
Câu 6:
Mã câu hỏi: 83357
Biết \(\mathop {\lim }\limits_{x \to - \infty } \frac{{x - m\sqrt {{x^2} + 2} }}{{x + 2}} = 2.\) Tìm m.
- A.1
- B.- 2
- C.3
- D.4
-
Câu 7:
Mã câu hỏi: 83358
Tìm m để hàm số \(y = \left\{ \begin{array}{l}
\frac{{{x^2} - 4}}{{x - 2}},\quad \quad x \ne 2\\
m,\quad \quad \quad \quad x = 2
\end{array} \right.\quad \) liên tục tại x = 2- A.1
- B.2
- C.4
- D.- 4
-
Câu 8:
Mã câu hỏi: 83359
Tính giới hạn \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {2x + 2} - 2x}}{{x - 1}}\)
- A.\( - \frac{1}{2}.\)
- B.2
- C.3
- D.\( - \frac{3}{2}.\)
-
Câu 9:
Mã câu hỏi: 83360
Biết \(\mathop {\lim }\limits_{x \to + \infty } f(x) = m;\mathop {\lim }\limits_{x \to + \infty } g(x) = n.\) Tính \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) + g(x)} \right]\)
- A.\(m+n\)
- B.\(m-n\)
- C.\(m\)
- D.\(n\)
-
Câu 10:
Mã câu hỏi: 83361
Biết \(\mathop {\lim }\limits_{x \to 2} f(x) = 3.\) Tính \(\mathop {\lim }\limits_{x \to 2} \left[ {f(x) + x} \right].\)
- A.5
- B.- 2
- C.1
- D.4
-
Câu 11:
Mã câu hỏi: 83362
Tính giới hạn \(\mathop {\lim }\limits_{x \to 1} \frac{{{{({x^2} + 2x - 2)}^5} - 1}}{{x - 1}}.\)
- A.1
- B.2
- C.3
- D.20
-
Câu 12:
Mã câu hỏi: 83363
Tính giới hạn \(\mathop {\lim }\limits_{} \frac{{n + 1}}{{{n^2} + 2}}.\)
- A.1
- B.2
- C.3
- D.0
-
Câu 13:
Mã câu hỏi: 83364
Tính giới hạn \(\mathop {\lim }\limits_{} \frac{{n + \sqrt {{n^2} + 1} }}{{n + 3}}.\)
- A.1
- B.2
- C.3
- D.4
-
Câu 14:
Mã câu hỏi: 83365
Cho dãy số \(u_n\) thỏa \(\mathop {\lim }\limits_{} {u_n} = 2.\) Tính \(\mathop {\lim }\limits_{} \left( {{u_n} + \frac{{{2^n}}}{{{2^n} + 3}}} \right).\)
- A.1
- B.2
- C.3
- D.4
-
Câu 15:
Mã câu hỏi: 83366
Cho dãy số \(u_n, v_n\) thỏa \(\mathop {\lim }\limits_{} {u_n} = 2,\mathop {\lim }\limits_{} {v_n} = 1.\) Tính \(\mathop {\lim }\limits_{} (2{u_n} - 3{v_n}).\)
- A.1
- B.2
- C.3
- D.7
-
Câu 16:
Mã câu hỏi: 83367
Tính đạo hàm của hàm số \(y = {x^2} + 1\)
- A.\(y' = {x^2} + 1\)
- B.\(y' = 2x + 1\)
- C.\(y' = 2x\)
- D.\(y' = 2x - 1\)
-
Câu 17:
Mã câu hỏi: 83368
Tính đạo hàm của hàm số \(y = \sin 2x\).
- A.\(y' = 2\sin x\)
- B.\(y' = \sin 2x\)
- C.\(y' = 2\cos x\)
- D.\(y' = 2\cos 2x\)
-
Câu 18:
Mã câu hỏi: 83369
Tính đạo hàm của hàm số \(y = {({x^2} + x)^2}\).
- A.\(y' = 3{({x^2} + x)^2}\)
- B.\(y' = 2x + 1\)
- C.\(y' = 2(2x + 1)\)
- D.\(y' = 2({x^2} + x)(2x + 1)\)
-
Câu 19:
Mã câu hỏi: 83370
Cho hàm số \(y = f(x) = {x^2} + mx\) (\(m\) là tham số) . Tìm \(m\), biết \(f'(1) = 3\).
- A.\(m=1\)
- B.\(m=2\)
- C.\(m=3\)
- D.\(m=7\)
-
Câu 20:
Mã câu hỏi: 83371
Cho hàm số \(y=\sin x\).Tính \(y''(0)\)
- A.\(y''(0) = 0.\)
- B.\(y''(0) = 1.\)
- C.\(y''(0) = 2.\)
- D.\(y''(0) = -2.\)
-
Câu 21:
Mã câu hỏi: 83372
Cho hàm số \(y=f(x)\) có đạo hàm trên tập số thực.Tìm hệ thức đúng?
- A.\(f'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}}.\)
- B.\(f'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x)}}{{x - 1}}.\)
- C.\(f'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x)}}{x}.\)
- D.\(f'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(1)}}{{x - 1}}.\)
-
Câu 22:
Mã câu hỏi: 83373
Cho hàm số \(y=f(x)\) có đạo hàm đến cấp 2 trên tập số thực.Tìm hệ thức đúng?
- A.\(f''(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}}.\)
- B.\(f''(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f'(x) - f'(1)}}{{x - 1}}.\)
- C.\(f''(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x)}}{x}.\)
- D.\(f''(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(1)}}{{x - 1}}.\)
-
Câu 23:
Mã câu hỏi: 83374
Tìm hệ số của x trong khai triển \({({x^2} + x + 2)^2}(x + 1)\) thành đa thức
- A.16
- B.6
- C.8
- D.2
-
Câu 24:
Mã câu hỏi: 83375
Tìm hệ số của x2 trong khai triển \({({x^2} + x + 2)^3}\) thành đa thức
- A.12
- B.18
- C.19
- D.20
-
Câu 25:
Mã câu hỏi: 83376
Hàm số \(y = (1 + x)\sqrt {1 - x} \) có đạo hàm \(y' = \frac{{ax + b}}{{2\sqrt {1 - x} }}\).Tính \(a+b\)
- A.- 2
- B.2
- C.- 3
- D.1
-
Câu 26:
Mã câu hỏi: 83377
Lập phương trình tiếp tuyến của đồ thị hàm số \(y = {x^2} + 3x + 1\) tại điểm có hoành độ bằng 1.
- A.y = 5x
- B.y = 5x+5
- C.y = 5x-5
- D.y = x
-
Câu 27:
Mã câu hỏi: 83378
Hàm số \(y = \frac{{\sqrt {{x^2} + 2x + 3} }}{x}\) có đạo hàm \(y' = \frac{{ax + b}}{{{x^2}\sqrt {{x^2} + 2x + 3} }}\).Tìm \(\max \left\{ {a,b} \right\}.\)
- A.2
- B.- 1
- C.- 3
- D.- 7
-
Câu 28:
Mã câu hỏi: 83379
Cho hàm số \(y=f(x)\) có đạo hàm trên tập số thực, biết \(f(3 - x) = {x^2} + x\).Tính \(f'(2)\)
- A.\(f'(2) = - 1.\)
- B.\(f'(2) = - 3.\)
- C.\(f'(2) = - 2.\)
- D.\(f'(2) = 3\)
-
Câu 29:
Mã câu hỏi: 83380
Tìm vi phân của hàm số \(y=x^3\)
- A.\(dy = {x^2}dx.\)
- B.\(dy = 3xdx.\)
- C.\(dy = 3{x^2}dx.\)
- D.\(dy = - 3{x^2}dx.\)
-
Câu 30:
Mã câu hỏi: 83381
Giải phương trình \(f''(x) = 0\), biết \(f(x) = {x^3} - 3{x^2}\).
- A.x = 0
- B.x = 2
- C.x = 0, x = 2
- D.x = 1
-
Câu 31:
Mã câu hỏi: 83382
Cho chuyển động thẳng xác định bởi phương trình \(s = {t^3} - 3{t^2} - 9t + 2\) ( t được tính bằng giây, s được tính bằng mét). Tìm gia tốc khi t = 2s.
- A.\(a = 12m/{s^2}.\)
- B.\(a = 6m/{s^2}.\)
- C.\(a = -9m/{s^2}.\)
- D.\(a = 2m/{s^2}.\)
-
Câu 32:
Mã câu hỏi: 83383
Tìm hệ số góc k của tiếp tuyến của đồ thị \(y = {x^3} - 2{x^2} - 3x + 1\) tại điểm có hoành độ bằng 0.
- A.k = -3
- B.k = 2
- C.k = 1
- D.k = 0
-
Câu 33:
Mã câu hỏi: 83384
Cho chuyển động thẳng xác định bởi phương trình \(s = {t^2} - 2t + 2\) ( t được tính bằng giây, s được tính bằng mét). Tính vận tốc tại thời điểm t = 3s.
- A.\(v = 2m/s.\)
- B.\(v = 4m/s.\)
- C.\(v = -2m/s.\)
- D.\(v = -4m/s.\)
-
Câu 34:
Mã câu hỏi: 83385
Tính \(d({\mathop{\rm s}\nolimits} {\rm{inx}} - x\cos x).\)
- A.\(d({\mathop{\rm s}\nolimits} {\rm{inx}} - x\cos x) = xsinxdx.\)
- B.\(d({\mathop{\rm s}\nolimits} {\rm{inx}} - x\cos x) = x{\mathop{\rm cosxdx}\nolimits} .\)
- C.\(d({\mathop{\rm s}\nolimits} {\rm{inx}} - x\cos x) = {\mathop{\rm cosxdx}\nolimits} .\)
- D.\(d({\mathop{\rm s}\nolimits} {\rm{inx}} - x\cos x) = sinxdx.\)
-
Câu 35:
Mã câu hỏi: 83386
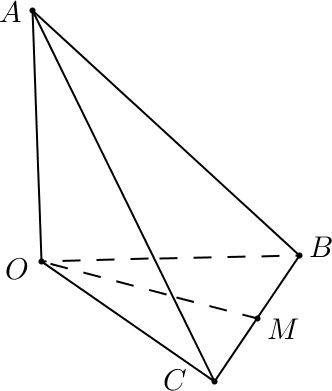
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC = 1. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
- A.\(90^0\)
- B.\(30^0\)
- C.\(60^0\)
- D.\(45^0\)
-
Câu 36:
Mã câu hỏi: 83387
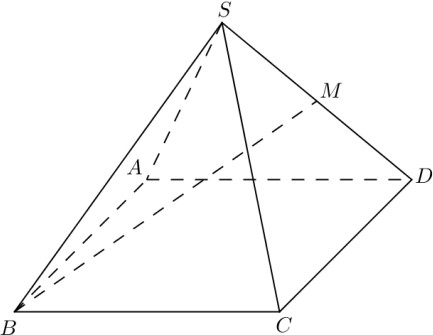
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm của SD (tham khảo hình vẽ bên).
Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng
- A.\(\frac{2}{3}.\)
- B.\(\frac{1}{3}.\)
- C.\(\frac{{\sqrt 3 }}{2}.\)
- D.\(\frac{{\sqrt 2 }}{2}.\)
-
Câu 37:
Mã câu hỏi: 83388
Cho tứ diện đều ABCD. Tìm góc giữa hai đường thẳng AB và CD.
- A.\(30^0\)
- B.\(45^0\)
- C.\(60^0\)
- D.\(90^0\)
-
Câu 38:
Mã câu hỏi: 83389
Giải bất phương trình \(f'(x) > 0\), biết \(f(x) = 2x + \sqrt {1 - {x^2}} .\)
- A.\(x \in \left( { - 1;\frac{1}{{\sqrt 2 }}} \right).\)
- B.\(x \in \left( { - 1;1} \right).\)
- C.\(x \in \left( { - 1;\frac{2}{{\sqrt 5 }}} \right).\)
- D.\(x \in \left( { - \frac{2}{{\sqrt 5 }};\frac{2}{{\sqrt 5 }}} \right).\)
-
Câu 39:
Mã câu hỏi: 83390
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a ( Tham khảo hình vẽ bên). Đường thẳng nào dưới đây vuông góc với mặt phẳng (ABCD) ?.
.png)
- A.SD
- B.SA
- C.SB
- D.SC
-
Câu 40:
Mã câu hỏi: 83391
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Đường thẳng nào dưới đây vuông góc với mặt phẳng (SAB) ?
- A.AB
- B.AC
- C.AD
- D.AS
-
Câu 41:
Mã câu hỏi: 83392
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Mặt phẳng nào dưới đây vuông góc với mặt phẳng (SAB) ?
- A.(SAB)
- B.(SAC)
- C.(SAD)
- D.(SCD)
-
Câu 42:
Mã câu hỏi: 83393
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Khoảng cách từ S đến mặt phẳng (ABCD) bằng
- A.SD
- B.SA
- C.SB
- D.SC
-
Câu 43:
Mã câu hỏi: 83394
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính tang của góc tạo bởi hai đường thẳng SB và CD
- A.3
- B.\(\sqrt 2 .\)
- C.\(\frac{{\sqrt 2 }}{3}.\)
- D.2
-
Câu 44:
Mã câu hỏi: 83395
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính khoảng cách giữa hai đường thẳng SA và BC.
- A.\(a\)
- B.\(\sqrt 2 a.\)
- C.\(2a\)
- D.\(3a\)
-
Câu 45:
Mã câu hỏi: 83396
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính tang của góc tạo bởi đường thẳng SC và mặt phẳng (ABCD)
- A.3
- B.\(\sqrt 2 .\)
- C.\(\frac{{\sqrt 2 }}{3}.\)
- D.2
-
Câu 46:
Mã câu hỏi: 83397
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính côsin của góc tạo bởi mặt phẳng (SBD) và mặt phẳng (ABCD).
- A.\(\frac{1}{3}.\)
- B.3
- C.\(\sqrt 2 .\)
- D.\(\frac{3}{{\sqrt 2 }}.\)
-
Câu 47:
Mã câu hỏi: 83398
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính khoảng cách từ điểm D đến đường thẳng SB.
- A.\(3a\)
- B.\(\frac{3}{5}a.\)
- C.\(\frac{{3\sqrt 5 }}{5}a.\)
- D.\(\frac{{\sqrt {21} a}}{3}.\)
-
Câu 48:
Mã câu hỏi: 83399
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Biết \(\overrightarrow {AC} = m\overrightarrow {AB} + n\overrightarrow {AD} + p\overrightarrow {AS} \). Tính tổng \(m+n+p\)
- A.3
- B.2
- C.1
- D.0
-
Câu 49:
Mã câu hỏi: 83400
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính khoảng cách từ điểm A đến mặt phẳng (SBC).
- A.\(a\)
- B.\(\sqrt 2 a.\)
- C.\(\frac{{2\sqrt 5 }}{5}a.\)
- D.\(\frac{{\sqrt {21} }}{3}a.\)
-
Câu 50:
Mã câu hỏi: 83401
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính khoảng cách từ điểm A đến mặt phẳng (SBD).
- A.\(2a\)
- B.\(\sqrt 2 a.\)
- C.\(\frac{2}{3}a.\)
- D.\(\frac{3}{2}a.\)
