Bài kiểm tra
Đề thi HK1 môn Toán 10 năm học 2019 - 2020 Trường THPT Vinh Lộc
1/50
90 : 00
Câu 1: style="box-sizing: border-box; margin: 0px 0px 10px; font-family: "Helvetica Neue", Helvetica, Arial, sans-serif;">Mệnh đề nào sau đây sai?
Câu 2: style="box-sizing: border-box; margin: 0px 0px 10px; font-family: "Helvetica Neue", Helvetica, Arial, sans-serif;">Cho parabol (P) có phương trình \(y = a{x^2} + bx + c\;\left( {a \ne 0} \right).\) Mệnh đề nào sau đây đúng?
Câu 3: style="box-sizing: border-box; margin: 0px 0px 10px; font-family: "Helvetica Neue", Helvetica, Arial, sans-serif;">Gọi M là trung điểm của đoạn thẳng AB. Khẳng định nào dưới đây là sai?
Câu 4: style="box-sizing: border-box; margin: 0px 0px 10px; font-family: "Helvetica Neue", Helvetica, Arial, sans-serif;">Giả sử phương trình \(2{x^2} - 4ax - 1 = 0\) có hai nghiệm . Tính giá trị của biểu thức \(T = \left| {{x_1} - {x_2}} \right|\).
Câu 5: style="box-sizing: border-box; margin: 0px 0px 10px; font-family: "Helvetica Neue", Helvetica, Arial, sans-serif;">Cho \(A = \left\{ {x \in R|\left| x \right| \ge 4} \right\}.\) Xác định \({C_R}A.\)
Câu 6: style="box-sizing: border-box; margin: 0px 0px 10px; font-family: "Helvetica Neue", Helvetica, Arial, sans-serif;">Tìm tất cả các giá trị của tham số để hàm số \(y = \frac{1}{{x - 3m}}\) xác định trên (1;2].
Câu 7: style="box-sizing: border-box; margin: 0px 0px 10px; font-family: "Helvetica Neue", Helvetica, Arial, sans-serif;">Cho hai vectơ \(\vec u\) và \(\vec v\) không cùng phương. Khi đó, cặp vectơ nào dưới đây cùng phương?
- A. \(\vec u = \frac{2}{3}\vec a + 3\vec b\) và \(\vec v = 2\vec a - 9\vec b\vec v = 2\vec a - 9\vec b\).
- B. \(\vec u = 2\vec a - 3\vec b\) và \(\vec v = - 2\vec a + 3\vec b\).
- C. \(\vec u = 2\vec a + 3\vec b\) và \(\vec v = \frac{1}{2}\vec a - 3\vec b\).
- D. \(\vec u = \frac{3}{5}\vec a + 3\vec b\) và \(\vec v = 2\vec a - \frac{3}{5}\vec b\).
Câu 8: style="box-sizing: border-box; margin: 0px 0px 10px; font-family: "Helvetica Neue", Helvetica, Arial, sans-serif;">Cho \(\overrightarrow a ,\overrightarrow b \ne \overrightarrow 0 .\) Khẳng định nào sau đây là sai?
- A. \({0^\circ } \le \left( {\overrightarrow a ,\overrightarrow b } \right) \le {90^\circ }.\)
- B. \(\,\left( {\overrightarrow a ,\overrightarrow b } \right) = \widehat {AOB}\) với \(\,\overrightarrow a = \overrightarrow {OA} ,\overrightarrow b = \overrightarrow {OB} .\)
- C. \(\left( {\overrightarrow a ,\overrightarrow b } \right) = \left( {\overrightarrow b ,\overrightarrow a } \right).\)
- D. \({0^\circ } \le \left( {\overrightarrow a ,\overrightarrow b } \right) \le {180^\circ }.\)
Câu 9: style="box-sizing: border-box; margin: 0px 0px 10px; font-family: "Helvetica Neue", Helvetica, Arial, sans-serif;">Trong các câu sau, câu nào là mệnh đề?
Câu 10: style="box-sizing: border-box; margin: 0px 0px 10px; font-family: "Helvetica Neue", Helvetica, Arial, sans-serif;">Cho Parabol \(\left( P \right):y = a{x^2} + bx + c\) có đồ thị bên dưới. Tìm trục đối xứng của (P)
.png)
Câu 11: Tìm điều kiện của phương trình \(\frac{{2x - 1}}{{x - 1}} = 3 - x.\)
Câu 12: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có B(9;7), C(11;-1). Gọi M, N lần lượt là trung điểm của AB, AC. Tìm tọa độ của vectơ \(\overrightarrow {MN} \).
Câu 13: Tìm tập xác định của hàm số \(y = \frac{3}{{\sqrt {4 - 2x} }}.\)
Câu 14: Cho 2 điểm A(-2;-3), B(4;7). Tìm điểm M thuộc trục tung sao cho ba điểm A, B, M thẳng hàng.
Câu 15: Cho a > 0, b > 0, c < 0. Khẳng định nào sau đây đúng?
Câu 16: Cho tam giác ABC. Vectơ \(\overrightarrow {AB} \) được phân tích theo hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BC} \). Đẳng thức nào dưới đây đúng?
- A. \(\overrightarrow {AB} = \overrightarrow {AC} - 2\overrightarrow {BC} .\)
- B. \(\overrightarrow {AB} = - \overrightarrow {AC} + \overrightarrow {BC} .\)
- C. \(\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {BC} \)
- D. \(\overrightarrow {AB} = \overrightarrow {AC} - \overrightarrow {BC} .\)
Câu 17: Cặp số nào dưới đây là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}
2x + 3y = 7\\
- x + 2y = 0
\end{array} \right.\)
Câu 18: Cho hàm số \(y = {x^2} - 4x + 2\). Khẳng định nào sau đây đúng?
Câu 19: Khẳng định nào sau đây là đúng?
- A. Tập hợp A là tập con của tập hợp B nếu mọi phần tử của A đều là phần tử của B
- B. Tập hợp A là tập con của tập hợp B nếu mọi phần tử của B đều là phần tử của A
- C. Tập hợp A là tập con của tập hợp B nếu có ít nhất một phần tử của A thuộc B
- D. Tập hợp A là tập con của tập hợp B nếu A có số phần tử ít hơn số phần tử của B
Câu 20: Cho tam giác ABC và đường thẳng d. Gọi O là điểm thỏa mãn hệ thức \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = \vec 0\). Tìm điểm M trên đường thẳng d sao cho vectơ \(\vec v = \overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} \) có độ dài nhỏ nhất.
Câu 21: Tìm phương trình của đường thẳng d: y = ax + b, biết d đi qua điểm A(1;1), cắt hai tia Ox, Oy và cách gốc tọa độ O một khoảng bằng \(\frac{{3\sqrt 5 }}{5}.\)
Câu 22: Tìm tọa độ vectơ \(\overrightarrow u \) biết \(\overrightarrow u + \overrightarrow b = \overrightarrow 0 ,\overrightarrow b = \left( {2; - 3} \right)\).
Câu 23: Tìm tất cả các giá trị của tham số thực m để hàm số \(y = \left( {6 - 2m} \right)x + 3m\) đồng biến trên R
Câu 24: Cho tập hợp \(A = \left( { - 2;2} \right],B = \left( {1;3} \right],C = \left[ {0;1} \right).\) Xác định \(\left( {A\backslash B} \right) \cap C.\)
Câu 25: Cho hai tập hợp \(A = \left\{ {0;1;2;3} \right\}\) và \(B = \left\{ { - 2;1;4} \right\}.\) Tìm \(A \cup B.\)
Câu 26: Trong mặt tọa độ Oxy, cho bốn điểm A(3;-2), B(7;1), C(0;1), D(-8;-5). Khẳng định nào dưới đây đúng?
Câu 27: Tính \(\sin {45^\circ }.\)
Câu 28: Cho 2 tập khác rỗng \(A = \left( {m - 2;m} \right),B = \left[ {3m - 1;3m + 3} \right].\) Tìm m để \(A \subset {C_R}B.\)
Câu 29: Phần tô đậm trong biểu đồ Ven dưới đây biểu diễn mối quan hệ nào giữa các tập hợp A, B, C?
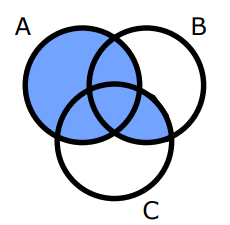
Câu 30: Với \(m \in \left( {a;b} \right)\) thì phương trình \(\sqrt {x - 1} \left( {{x^2} - 3x - m} \right) = 0\) có ba nghiệm phân biệt. Tính giá trị của biểu thức \(P = b - 4a\).
Câu 31: Cho hàm số y = 2x - 9 có đồ thị là đường thẳng \(\Delta \). Đường thẳng \(\Delta \) cắt hai trục tọa độ tại hai điểm A, B. Tính diện tích tam giác OAB.
Câu 32: Cho mệnh đề “Phương trình \({x^2} + 1 = 0\) vô nghiệm”. Viết lại mệnh đề trên bằng cách sử dụng kí hiệu \(\forall \) hoặc \(\exists .\)
Câu 33: Tìm tập nghiệm S của phương trình \(2x + \frac{3}{{x - 1}} = \frac{{3x}}{{x - 1}}\)
Câu 35: Phương trình nào dưới đây tương đương với phương trình \(f\left( x \right) = g\left( x \right)?\)
Câu 36: Tìm điều kiện của a, b, c để hàm số \(f(x) = a{x^2} + bx + c\) là hàm số chẵn.
Câu 37: Cho \(\vec u = 2\vec i - \vec j\) và \(\vec v = \vec i + x\). Xác định x sao cho \(\vec u\) và \(\vec v\) cùng phương.
Câu 38: Có ba lớp học sinh 10A, 10B, 10C gồm 128 em cùng tham gia lao động trồng cây. Mỗi em lớp 10A trồng được 3 cây bạch đàn và 4 cây bàng. Mỗi em lớp 10B trồng được 2 cây bạch đàn và 5 cây bàng. Mỗi em lớp 10C trồng được 6 cây bạch đàn. Cả ba lớp trồng được là 476 cây bạch đàn và 375 cây bàng. Hỏi mỗi lớp có bao nhiêu học sinh ?
Câu 39: Với \(m \in \left[ {a;b} \right]\) thì hệ phương trình \(\left\{ \begin{array}{l}
\sqrt {7x + y} + \sqrt {x + y} = 6\\
\sqrt {x + y} - y + x = m
\end{array} \right.\) có nghiệm . Tính giá trị của biểu thức \(T = a + 4b.\)
Câu 40: Cho vectơ \(\overrightarrow {ED} \) (khác vectơ không). Chọn khẳng định đúng?
Câu 41: Trong hệ trục tọa độ \(\left( {O;\overrightarrow i ;\overrightarrow j } \right)\), cho vectơ \(\overrightarrow a = \left( { - 2;3} \right)\). Tọa độ vectơ \(\overrightarrow b = 2\overrightarrow a + \overrightarrow i \) là
Câu 42: Kí hiệu nào sau đây để chỉ 2019 là một số tự nhiên?
Câu 43: Vectơ có điểm đầu là M và điểm cuối là N được kí hiệu là
Câu 44: Cho mệnh đề "\(\exists x \in R,{x^2} < x\)". Mệnh đề phủ định của mệnh đề đã cho là
Câu 45: Trong các tập hợp sau, tập hợp nào có đúng 2 tập hợp con?
Câu 46: Tập xác định D của hàm số \(y = \frac{1}{{x - 2}}\) là
Câu 47: Cho \(A = \left( { - \infty ;2} \right)\), \(B = \left( {0; + \infty } \right)\). Đặt \(C = A\backslash B\). Khi đó
Câu 48: Cho ba điểm A, B, C bất kỳ. Chọn đẳng thức đúng trong các đẳng thức sau
Câu 49: Cho phương trình \({x^4} - 3{x^2} + 2 = 0\). Hỏi phương trình đã cho có tất cả bao nhiêu nghiệm?
Câu 50: Nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}
{x + 3y = 8}\\
{3x + y = 6}
\end{array}} \right.\) có dạng \(\left( {{x_0};{y_0}} \right)\). Tính \(T = {x_0} + {y_0}\).




