Đề thi HK1 môn Toán 10 năm học 2019 - 2020 Trường THPT Vinh Lộc

Câu hỏi Trắc nghiệm (50 câu):

• Câu 1:

  Mã câu hỏi: 1291

  Mệnh đề nào sau đây sai?

  • A.$\overrightarrow{AA}=\overrightarrow{0}$. 
  • B.$\overrightarrow{0}$ cùng hướng với mọi vectơ.
  • C.$\overrightarrow{0}$ cùng phương với mọi vectơ.
  • D.$\left|\overrightarrow{AB}\right|$ là một số dương.

• Câu 2:

  Mã câu hỏi: 1295

  Cho parabol (P) có phương trình $y=a{x}^2+bx+c\left(a\ne 0\right).$ Mệnh đề nào sau đây đúng?

  • A.Tung độ đỉnh của (P) là $\frac{\mathrm{\Delta }}{4a}.$
  • B.Tung độ đỉnh của (P) là $-\frac{b}{2a}.$
  • C.Hoành độ đỉnh (P) là $-\frac{b}{2a}.$
  • D.Hoành độ đỉnh của (P) là $\frac{-\mathrm{\Delta }}{4a}.$

• Câu 3:

  Mã câu hỏi: 1298

  Gọi M là trung điểm của đoạn thẳng AB. Khẳng định nào dưới đây là sai?

  • A.$\overrightarrow{MA}=\overrightarrow{MB}$.
  • B.$\overrightarrow{AB}=2\overrightarrow{MB}.$
  • C.$\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}$. 
  • D.$\overrightarrow{MA}=-\frac{1}{2}\overrightarrow{AB}$.

• Câu 4:

  Mã câu hỏi: 1301

  Giả sử phương trình $2x^2-4ax-1=0$ có hai nghiệm . Tính giá trị của biểu thức $T=\left|x_1-x_2\right|$.

  • A.$T=\frac{4a^2+2}{3}.$
  • B.$T=\frac{\sqrt{a^2+8}}{4}.$
  • C.$T=\frac{\sqrt{a^2+8}}{2}.$
  • D.$T=\sqrt{4a^2+2}.$

• Câu 5:

  Mã câu hỏi: 1303

  Cho $A=\left\{x\in R|\left|x\right|\ge 4\right\}.$ Xác định $C_{R}A.$

  • A.$\left(-\mathrm{\infty };-4\right)\cup \left(4;+\mathrm{\infty }\right).$
  • B.$\left(-\mathrm{\infty };-4\right]\cup \left[4;+\mathrm{\infty }\right).$
  • C.[-4;4]
  • D.(-4;4)

• Câu 6:

  Mã câu hỏi: 1306

  Tìm tất cả các giá trị của tham số để hàm số $y=\frac{1}{x-3m}$ xác định trên (1;2].

  • A.$m\le \frac{1}{3}$  hoặc $m>\frac{2}{3}.$ 
  • B.$\frac{1}{3}<m.$ 
  • C.$m>\frac{2}{3}.$
  • D.$\frac{1}{3}<m\le \frac{2}{3}.$

• Câu 7:

  Mã câu hỏi: 1308

  Cho hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ không cùng phương. Khi đó, cặp vectơ nào dưới đây cùng phương?

  • A.$\overrightarrow{u}=\frac{2}{3}\overrightarrow{a}+3\overrightarrow{b}$ và $\overrightarrow{v}=2\overrightarrow{a}-9\overrightarrow{b}\overrightarrow{v}=2\overrightarrow{a}-9\overrightarrow{b}$.
  • B.$\overrightarrow{u}=2\overrightarrow{a}-3\overrightarrow{b}$ và $\overrightarrow{v}=-2\overrightarrow{a}+3\overrightarrow{b}$.
  • C.$\overrightarrow{u}=2\overrightarrow{a}+3\overrightarrow{b}$ và $\overrightarrow{v}=\frac{1}{2}\overrightarrow{a}-3\overrightarrow{b}$. 
  • D.$\overrightarrow{u}=\frac{3}{5}\overrightarrow{a}+3\overrightarrow{b}$ và $\overrightarrow{v}=2\overrightarrow{a}-\frac{3}{5}\overrightarrow{b}$.

• Câu 8:

  Mã câu hỏi: 1310

  Cho $\overrightarrow{a},\overrightarrow{b}\ne \overrightarrow{0}.$ Khẳng định nào sau đây là sai?

  • A.$0^{\circ }\le \left(\overrightarrow{a},\overrightarrow{b}\right)\le {90}^{\circ }.$
  • B.$\left(\overrightarrow{a},\overrightarrow{b}\right)=\widehat{AOB}$ với $\overrightarrow{a}=\overrightarrow{OA},\overrightarrow{b}=\overrightarrow{OB}.$
  • C.$\left(\overrightarrow{a},\overrightarrow{b}\right)=\left(\overrightarrow{b},\overrightarrow{a}\right).$
  • D.$0^{\circ }\le \left(\overrightarrow{a},\overrightarrow{b}\right)\le {180}^{\circ }.$

• Câu 9:

  Mã câu hỏi: 1313

  Trong các câu sau, câu nào là mệnh đề?

  • A.Mấy giờ rồi? 
  • B.17 là số lẻ.  
  • C.Nóng quá!
  • D.x + y > 8

• Câu 10:

  Mã câu hỏi: 1315

  Cho Parabol $\left(P\right):y=a{x}^2+bx+c$ có đồ thị bên dưới. Tìm trục đối xứng của (P)

  

  • A.y = 3
  • B.x = 3
  • C.x = 1
  • D.y = 1

• Câu 11:

  Mã câu hỏi: 1318

  Tìm điều kiện của phương trình $\frac{2x-1}{x-1}=3-x.$

  • A.$x\ne 1$
  • B.x > 0
  • C.x > 1
  • D.$x\ne 0$

• Câu 12:

  Mã câu hỏi: 1320

  Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có B(9;7), C(11;-1). Gọi M, N lần lượt là trung điểm của AB, AC. Tìm tọa độ của vectơ $\overrightarrow{MN}$.

  • A.(10;6)
  • B.(1;-4)
  • C.(2;-8)
  • D.(5;3)

• Câu 13:

  Mã câu hỏi: 1322

  Tìm tập xác định của hàm số $y=\frac{3}{\sqrt{4-2x}}.$

  • A.R\{-2}
  • B.$\left(-\mathrm{\infty };2\right)$
  • C.$\left(-\mathrm{\infty };2\right]$
  • D.R\{2}

• Câu 14:

  Mã câu hỏi: 1325

  Cho 2 điểm A(-2;-3), B(4;7). Tìm điểm M thuộc trục tung sao cho ba điểm A, B, M thẳng hàng.

  • A.$M\left(0;\frac{4}{3}\right)$
  • B.M(0;1)
  • C.$M\left(0;\frac{1}{3}\right)$
  • D.$M\left(0;-\frac{1}{3}\right)$

• Câu 15:

  Mã câu hỏi: 1327

  Cho a > 0, b > 0, c < 0. Khẳng định nào sau đây đúng?

  • A.Phương trình $a{x}^2+bx+c=0$ có một nghiệm duy nhất.
  • B.Phương trình $a{x}^2+bx+c=0$ có hai nghiệm dương phân biệt.
  • C.Phương trình $a{x}^2+bx+c=0$ có hai nghiệm âm phân biệt.
  • D.Phương trình $a{x}^2+bx+c=0$ có hai nghiệm trái dấu.

• Câu 16:

  Mã câu hỏi: 1329

  Cho tam giác ABC. Vectơ $\overrightarrow{AB}$ được phân tích theo hai vectơ $\overrightarrow{AC}$ và $\overrightarrow{BC}$. Đẳng thức nào dưới đây đúng?

  • A.$\overrightarrow{AB}=\overrightarrow{AC}-2\overrightarrow{BC}.$
  • B.$\overrightarrow{AB}=-\overrightarrow{AC}+\overrightarrow{BC}.$
  • C.$\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{BC}$
  • D.$\overrightarrow{AB}=\overrightarrow{AC}-\overrightarrow{BC}.$

• Câu 17:

  Mã câu hỏi: 1332

  Cặp số nào dưới đây là nghiệm của hệ phương trình $\{\begin{array}{l}2x+3y=7\\ -x+2y=0\end{array}$

  • A.$\left(x;y\right)=\left(2;1\right).$
  • B.$\left(x;y\right)=\left(-1;2\right).$
  • C.$\left(x;y\right)=\left(1;2\right).$
  • D.$\left(x;y\right)=\left(-2;1\right).$

• Câu 18:

  Mã câu hỏi: 1334

  Cho hàm số $y=x^2-4x+2$. Khẳng định nào sau đây đúng?

  • A.Hàm số đồng biến trên khoảng $\left(2;+\mathrm{\infty }\right)$. 
  • B.Hàm số đồng biến trên khoảng $\left(-\mathrm{\infty };2\right)$.
  • C.Hàm số nghịch biến trên khoảng $\left(-\mathrm{\infty };-2\right)$.
  • D.Hàm số đồng biến trên khoảng $\left(-2;+\mathrm{\infty }\right)$.

• Câu 19:

  Mã câu hỏi: 1336

  Khẳng định nào sau đây là đúng?

  • A.Tập hợp A là tập con của tập hợp B nếu mọi phần tử của A đều là phần tử của B
  • B.Tập hợp A là tập con của tập hợp B nếu mọi phần tử của B đều là phần tử của A
  • C.Tập hợp A là tập con của tập hợp B nếu có ít nhất một phần tử của A thuộc B
  • D.Tập hợp A là tập con của tập hợp B nếu A có số phần tử ít hơn số phần tử của B

• Câu 20:

  Mã câu hỏi: 1339

  Cho tam giác ABC và đường thẳng d. Gọi O là điểm thỏa mãn hệ thức $\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}=\overrightarrow{0}$. Tìm điểm M trên đường thẳng d sao cho vectơ $\overrightarrow{v}=\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}$ có độ dài nhỏ nhất.

  • A.Điểm M là hình chiếu vuông góc của O trên d.    
  • B.Điểm M là hình chiếu vuông góc của A trên d.
  • C.Điểm M là hình chiếu vuông góc của B trên d.   
  • D.Điểm M là giao điểm của AB và d.

• Câu 21:

  Mã câu hỏi: 1341

  Tìm phương trình của đường thẳng d: y = ax + b, biết d đi qua điểm A(1;1), cắt hai tia Ox, Oy và cách gốc tọa độ O một khoảng bằng $\frac{3\sqrt{5}}{5}.$

  • A.$y=-2x+1$
  • B.$y=2x-1$
  • C.$y=-2x+3$
  • D.$y=-2x-3$

• Câu 22:

  Mã câu hỏi: 1343

  Tìm tọa độ vectơ $\overrightarrow{u}$ biết $\overrightarrow{u}+\overrightarrow{b}=\overrightarrow{0},\overrightarrow{b}=\left(2;-3\right)$.

  • A.(2;-3)
  • B.(2;3)
  • C.(-2;3)
  • D.(-2;-3)

• Câu 23:

  Mã câu hỏi: 1345

  Tìm tất cả các giá trị của tham số thực m để hàm số $y=\left(6-2m\right)x+3m$ đồng biến trên R

  • A.$m<\frac{1}{3}.$
  • B.$m\le 3.$
  • C.$m\le \frac{1}{3}.$
  • D.m < 3

• Câu 24:

  Mã câu hỏi: 1346

  Cho tập hợp $A=\left(-2;2\right],B=\left(1;3\right],C=\left[0;1\right).$ Xác định $\left(A\mathrm{\setminus }B\right)\cap C.$

  • A.(-2;5]
  • B.[0;1)
  • C.{0}
  • D.{0;1}

• Câu 25:

  Mã câu hỏi: 1347

  Cho hai tập hợp $A=\left\{0;1;2;3\right\}$ và $B=\left\{-2;1;4\right\}.$ Tìm $A\cup B.$

  • A.$A\cup B=\left\{0;2;3\right\}.$
  • B.$A\cup B=\left\{1\right\}.$
  • C.$A\cup B=\left\{0;1;2;3;4\right\}.$
  • D.$A\cup B=\left\{-2;0;1;2;3;4\right\}.$

• Câu 26:

  Mã câu hỏi: 1348

  Trong mặt tọa độ Oxy, cho bốn điểm A(3;-2), B(7;1), C(0;1), D(-8;-5). Khẳng định nào dưới đây đúng?

  • A.$\overrightarrow{AB},\overrightarrow{CD}$ cùng hướng
  • B.A, B, C, D thẳng hàng
  • C.$\overrightarrow{AB},\overrightarrow{CD}$ ngược hướng
  • D.$\overrightarrow{AB},\overrightarrow{CD}$ là hai vectơ đối nhau.

• Câu 27:

  Mã câu hỏi: 1349

  Tính $\sin {45}^{\circ }.$

  • A.1
  • B.$\frac{\sqrt{2}}{2}.$
  • C.$\frac{\sqrt{3}}{2}.$
  • D.$\frac{1}{2}.$

• Câu 28:

  Mã câu hỏi: 1350

  Cho 2 tập khác rỗng $A=\left(m-2;m\right),B=\left[3m-1;3m+3\right].$ Tìm m để $A\subset C_{R}B.$

  • A.$-\frac{5}{2}\le m\le \frac{1}{2}.$
  • B.$[\begin{array}{l}m<-\frac{5}{2}\\ m>\frac{1}{2}\end{array}.$
  • C.$-\frac{5}{2}<m<\frac{1}{2}.$
  • D.$[\begin{array}{l}m\le -\frac{5}{2}\\ m\ge \frac{1}{2}\end{array}.$

• Câu 29:

  Mã câu hỏi: 1351

  Phần tô đậm trong biểu đồ Ven dưới đây biểu diễn mối quan hệ nào giữa các tập hợp A, B, C?

  

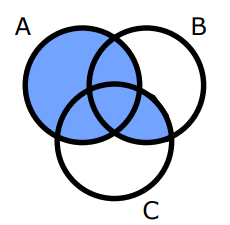
  • A.$A\cap B\cap C.$
  • B.$A\cup \left(B\cap C\right).$
  • C.$\left(A\cap B\right)\cup C.$
  • D.$A\cup B\cup C.$

• Câu 30:

  Mã câu hỏi: 1352

  Với $m\in \left(a;b\right)$ thì phương trình $\sqrt{x-1}\left(x^2-3x-m\right)=0$ có ba nghiệm phân biệt. Tính giá trị của biểu thức $P=b-4a$.

  • A.P = 8
  • B.P = 10
  • C.P = 9
  • D.P = 7

• Câu 31:

  Mã câu hỏi: 1353

  Cho hàm số y = 2x - 9 có đồ thị là đường thẳng $\mathrm{\Delta }$. Đường thẳng $\mathrm{\Delta }$ cắt hai trục tọa độ tại hai điểm A, B. Tính diện tích tam giác OAB.

  • A.$-\frac{81}{4}$
  • B.18
  • C.$\frac{81}{2}$
  • D.$\frac{81}{4}$

• Câu 32:

  Mã câu hỏi: 1354

  Cho mệnh đề “Phương trình $x^2+1=0$ vô nghiệm”. Viết lại mệnh đề trên bằng cách sử dụng kí hiệu $\mathrm{\forall }$ hoặc $\mathrm{\exists }.$

  • A.$\mathrm{\exists }x\in R:x^2+1\ne 0.$
  • B.$\mathrm{\forall }x\in R:x^2+1\ne 0.$
  • C.$\mathrm{\forall }x\in R:x^2+1=0.$
  • D.$\mathrm{\exists }x\in R:x^2+1<0.$

• Câu 33:

  Mã câu hỏi: 1355

  Tìm tập nghiệm S của phương trình $2x+\frac{3}{x-1}=\frac{3x}{x-1}$

  • A.$S=\mathrm{\varnothing }.$
  • B.$S=\left\{\frac{3}{2}\right\}.$
  • C.$S=\left\{0;\frac{3}{2}\right\}.$
  • D.$S=\left\{1;\frac{3}{2}\right\}.$

• Câu 34:

  Mã câu hỏi: 1356

  Quy tròn số 3,1463 đến hàng phần trăm.

  • A.3,14
  • B.3,146
  • C.3,15
  • D.3,156

• Câu 35:

  Mã câu hỏi: 1357

  Phương trình nào dưới đây tương đương với phương trình $f\left(x\right)=g\left(x\right)?$

  • A.${\left(f\left(x\right)\right)}^3={\left(g\left(x\right)\right)}^3.$
  • B.${\left(f\left(x\right)\right)}^2={\left(g\left(x\right)\right)}^2$
  • C.$\sqrt{f\left(x\right)}=\sqrt{g\left(x\right)}.$
  • D.$\frac{f\left(x\right)}{g\left(x\right)}=1.$

• Câu 36:

  Mã câu hỏi: 1358

  Tìm điều kiện của a, b, c để hàm số $f(x)=a{x}^2+bx+c$ là hàm số chẵn. 

  • A.$a,b\in R,c=0$
  • B.$a,c\in R,b=0$
  • C.$a\in R,b=0,c=0$
  • D.$a,b,c\in R$

• Câu 37:

  Mã câu hỏi: 1359

  Cho $\overrightarrow{u}=2\overrightarrow{i}-\overrightarrow{j}$ và $\overrightarrow{v}=\overrightarrow{i}+x$. Xác định x sao cho $\overrightarrow{u}$ và $\overrightarrow{v}$ cùng phương.

  • A.$x=\frac{1}{4}$
  • B.$x=-\frac{1}{2}$
  • C.x = 2
  • D.x = - 1

• Câu 38:

  Mã câu hỏi: 1360

  Có ba lớp học sinh 10A, 10B, 10C gồm 128 em cùng tham gia lao động trồng cây. Mỗi em lớp 10A trồng được 3 cây bạch đàn và 4 cây bàng. Mỗi em lớp 10B trồng được 2 cây bạch đàn và 5 cây bàng. Mỗi em lớp 10C trồng được 6 cây bạch đàn. Cả ba lớp trồng được là 476 cây bạch đàn và 375 cây bàng. Hỏi mỗi lớp có bao nhiêu học sinh ?

  • A.10 A có 45 em, 10B lớp có 40 em, 10C lớp có 43 em
  • B.10 A có 45 em, 10B lớp có 43 em, 10C lớp có 40 em
  • C.10 A có 40 em, 10B lớp có 43 em, 10C lớp có 45 em
  • D.10 A có 43 em, 10B lớp có 40 em, 10C lớp có 45 em

• Câu 39:

  Mã câu hỏi: 1361

  Với $m\in \left[a;b\right]$ thì hệ phương trình $\{\begin{array}{l}\sqrt{7x+y}+\sqrt{x+y}=6\\ \sqrt{x+y}-y+x=m\end{array}$ có nghiệm . Tính giá trị của biểu thức $T=a+4b.$

  • A.T = 16
  • B.T = 6
  • C.T = 8
  • D.T = 18

• Câu 40:

  Mã câu hỏi: 1362

  Cho vectơ $\overrightarrow{ED}$ (khác vectơ không). Chọn khẳng định đúng?

  • A.Độ dài của đoạn thẳng ED là phương của vectơ $\overrightarrow{ED}$
  • B.Độ dài của đoạn thẳng ED là giá của vectơ $\overrightarrow{ED}$
  • C.Độ dài của đoạn thẳng ED là độ dài của vectơ $\overrightarrow{ED}$
  • D.Độ dài của đoạn thẳng ED là hướng của vectơ $\overrightarrow{ED}$

• Câu 41:

  Mã câu hỏi: 1363

  Trong hệ trục tọa độ $\left(O;\overrightarrow{i};\overrightarrow{j}\right)$, cho vectơ $\overrightarrow{a}=\left(-2;3\right)$. Tọa độ vectơ $\overrightarrow{b}=2\overrightarrow{a}+\overrightarrow{i}$ là

  • A.$\overrightarrow{b}=\left(-3;6\right)$
  • B.$\overrightarrow{b}=\left(-4;6\right)$
  • C.$\overrightarrow{b}=\left(-4;7\right)$
  • D.$\overrightarrow{b}=\left(-3;7\right)$

• Câu 42:

  Mã câu hỏi: 1364

  Kí hiệu nào sau đây để chỉ 2019 là một số tự nhiên?

  • A.$2019\in N$
  • B.$2019\subset N$
  • C.$2019<N$
  • D.$2019\notin N$

• Câu 43:

  Mã câu hỏi: 1365

  Vectơ có điểm đầu là M và điểm cuối là N được kí hiệu là

  • A.$\overrightarrow{NM}$
  • B.$\overrightarrow{NN}$
  • C.$\overrightarrow{MM}$
  • D.$\overrightarrow{MN}$

• Câu 44:

  Mã câu hỏi: 1366

  Cho mệnh đề "$\mathrm{\exists }x\in R,x^2<x$". Mệnh đề phủ định của mệnh đề đã cho là

  • A."$\mathrm{\forall }x\in R,x^2>x$"
  • B."$\mathrm{\forall }x\in R,x^2\ge x$"
  • C."$\mathrm{\exists }x\in R,x^2\ge x$"
  • D."$\mathrm{\exists }x\in R,x^2<x$"

• Câu 45:

  Mã câu hỏi: 1367

  Trong các tập hợp sau, tập hợp nào có đúng 2 tập hợp con?

  • A.$A=\left\{0;1;2\right\}$
  • B.$A=\left\{1;2\right\}$
  • C.$A=\mathrm{\varnothing }$
  • D.$A=\left\{1\right\}$

• Câu 46:

  Mã câu hỏi: 1368

  Tập xác định D của hàm số $y=\frac{1}{x-2}$ là

  • A.D = R\{2}
  • B.D = {2}
  • C.D = N\{2}
  • D.D = R

• Câu 47:

  Mã câu hỏi: 1369

  Cho $A=\left(-\mathrm{\infty };2\right)$, $B=\left(0;+\mathrm{\infty }\right)$. Đặt $C=A\mathrm{\setminus }B$. Khi đó

  • A.$C=\left(-\mathrm{\infty };0\right)$
  • B.$C=\left(0;2\right)$
  • C.$C=\left(-\mathrm{\infty };0\right]$
  • D.$C=\left(0;2\right]$

• Câu 48:

  Mã câu hỏi: 1370

  Cho ba điểm A, B, C bất kỳ. Chọn đẳng thức đúng trong các đẳng thức sau

  • A.$\overrightarrow{AC}+\overrightarrow{BA}=\overrightarrow{CB}$
  • B.$\overrightarrow{AA}+\overrightarrow{CC}=\overrightarrow{AC}$
  • C.$\overrightarrow{AC}+\overrightarrow{BA}=\overrightarrow{BC}$
  • D.$\overrightarrow{AC}+\overrightarrow{BA}=\overrightarrow{0}$

• Câu 49:

  Mã câu hỏi: 1371

  Cho phương trình $x^4-3x^2+2=0$. Hỏi phương trình đã cho có tất cả bao nhiêu nghiệm?

  • A.3 nghiệm
  • B.4 nghiệm
  • C.2 nghiệm
  • D.1 nghiệm

• Câu 50:

  Mã câu hỏi: 1372

  Nghiệm của hệ phương trình $\{\begin{array}{c}x+3y=8\\ 3x+y=6\end{array}$ có dạng $\left(x_0;y_0\right)$. Tính $T=x_0+y_0$.

  • A.T = 6
  • B.T = 2
  • C.$T=\frac{7}{2}$
  • D.$T=\frac{7}{4}$