Đề thi HK1 môn Toán 10 năm 2020 trường THPT Thủ Khoa Huân

Câu 2: Trong các mệnh đề sau, mệnh đề nào không phải là định lí?

Câu 3: Trong các tập hợp sau, tập nào là tập rỗng?

Câu 4: Cho các tập hợp \(A = \left\{ {x \in R|\,x < 3} \right\}\), \(B = \left\{ {x \in R|1 < x \le 5} \right\}\), \(C = \left\{ {x \in R| - 2 \le x \le 4} \right\}\). Tính \(\left( {B \cup C} \right)\backslash \left( {A \cap C} \right).\)

Câu 5: Cho \(A = \left( { - \infty ;2} \right]\), \(B = \left[ {2; + \infty } \right)\), \(C = \left( {0;3} \right)\). Chọn phát biểu sai.

Câu 6: Cho số thực a < 0. Tìm điều kiện cần và đủ để \(\left( { - \infty ;9a} \right) \cap \left( {\frac{4}{a}; + \infty } \right) \ne \emptyset \).

Câu 7: Tập hợp nào dưới đây là giao của hai tập hợp \(A = \left\{ {x \in : - 1 \le x < 3} \right\}\), \(B = \left\{ {x \in R:\left| x \right| < 2} \right\}\)?

Câu 8: Cho \(A = \left[ {1; + \infty } \right)\), \(B = \left\{ {x \in R|{x^2} + 1 = 0} \right\}\), \(C = \left( {0;4} \right)\). Tập \(\left( {A \cup B} \right) \cap C\) có bao nhiêu phần tử là số nguyên.

Câu 9: Phương trình \(\left| {3x - 1} \right| = 2x - 5\) có bao nhiêu nghiệm?

Câu 10: Cho tam giác ABC có G là trọng tâm. Mệnh đề nào sau đây sai?

Câu 11: Trong mặt phẳng Oxy, cho \(A\left( {2; - 3} \right)\), \(B\left( {3;4} \right)\). Tìm tọa độ điểm M nằm trên trục hoành sao cho A, B, M thẳng hàng.

Câu 12: Theo thống kê, dân số Việt Nam năm 2016 được ghi lại như sau \(\overline S = 94\,\,444\,\,200 \pm 3000\) (người). Số quy tròn của số gần đúng \(94\,\,444\,\,200\) bằng bao nhiêu?

Câu 13: Tìm TXĐ của hàm số \(y = \sqrt {2 - x} + \sqrt {7 + x} \).

Câu 14: Tập xác định của hàm số \(y = \left\{ \begin{array}{l} \sqrt {3 - x} \,\,,\,\,x \in \left( { - \infty ;0} \right)\\ \sqrt {\frac{1}{x}} \,\,\,\,\,\,\,\,,\,\,x \in \left( {0; + \infty } \right) \end{array} \right.\) là tập nào dưới đây?

Câu 15: Trong các hàm số sau đây: y = |x|; \(y = {x^2} + 4x\); \(y = - {x^4} + 2{x^2}\) có bao nhiêu hàm số chẵn?

Câu 16: Cho hàm số y = x - 2. Khẳng định nào sau đây là khẳng định sai?

Câu 17: Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l} {x^2} + 3x{\rm{\ khi \ }}x \ge 0\\ 1 - x{\rm{\ khi \ }}x < 0 \end{array} \right.\). Khi đó, \(f\left( 1 \right) + f\left( { - 1} \right)\) bằng bao nhiêu?

Câu 18: Một hàm số bậc nhất y = f(x) có \(f\left( { - 1} \right) = 2,f\left( 2 \right) = - 3\). Hỏi hàm số đó là hàm số nào dưới đây?

Câu 19: Với những giá trị nào của m thì hàm số \(f\left( x \right) = \left( {m + 1} \right)x + 2\) đồng biến?

Câu 20: Cho hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) lần lượt có phương trình: \(mx + \left( {m - 1} \right)y - 2\left( {m + 2} \right) = 0\) và \(3mx - \left( {3m + 1} \right)y - 5m - 4 = 0\). Xác định vị trí tương đối của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) khi \(m = \frac{1}{3}\).

Câu 21: Cho parabol \(\left( P \right):y = a{x^2} + bx + c\) có đồ thị như hình bên. Phương trình của parabol này là phương trình nào dưới đây?

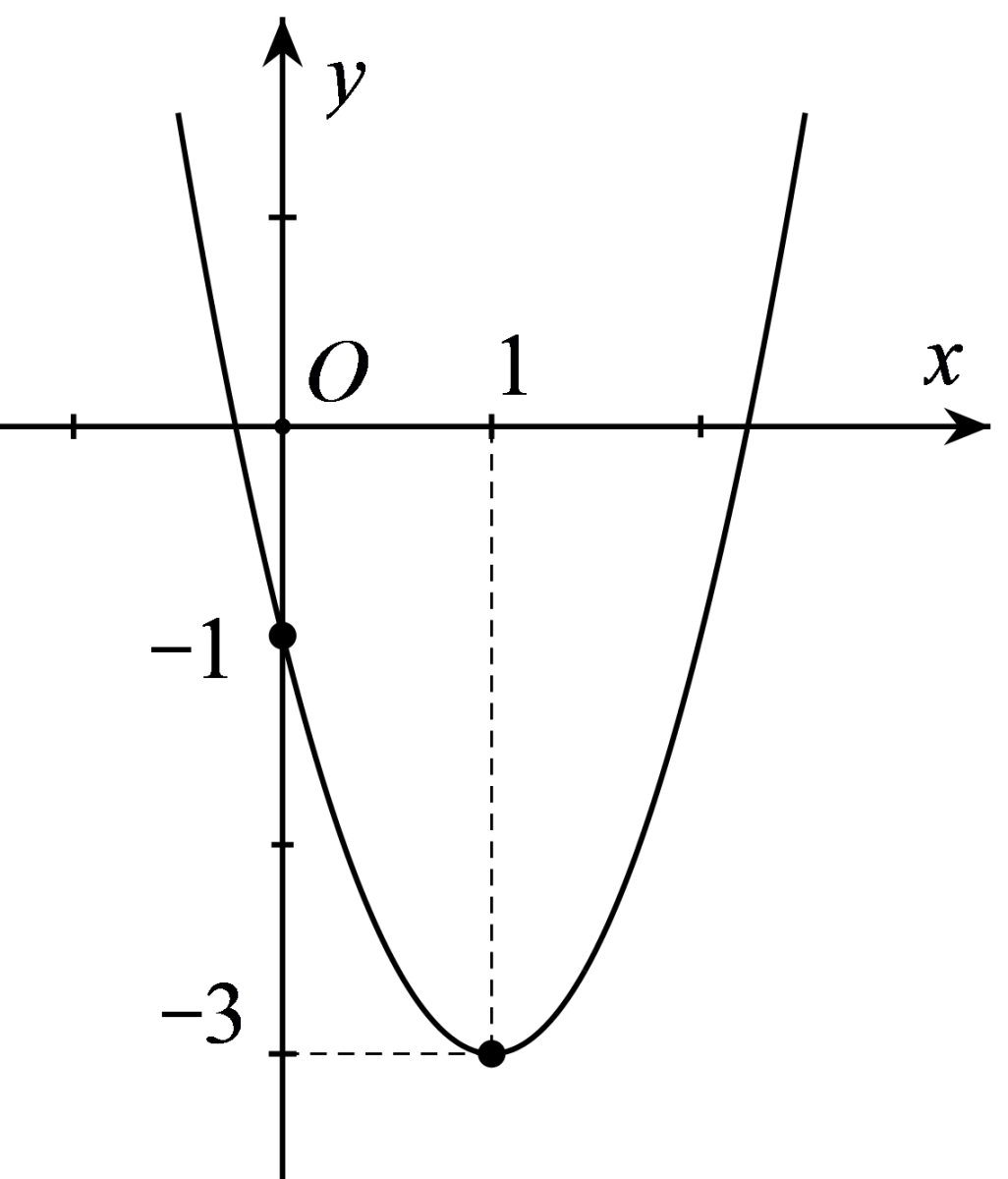
Câu 22: Hàm số nào sau đây có giá trị nhỏ nhất tại \(x = \frac{3}{4}\)?

Câu 23: Parabol \(y = a{x^2} + bx + 2\) đi qua hai điểm M(1; 5) và N(-2; 8) có phương trình là phương trình nào dưới đây?

Câu 24: Parabol \(y = a{x^2} + bx + c\) đi qua A(8;0) và có đỉnh S(6;-12) có phương trình là phương trình nào dưới đây?

Câu 25: Tìm giao điểm của parabol \(y = {x^2} - 3{\rm{x}} + 2\) với đường thẳng \(y = x - 1\).

Câu 26: Trong bốn phép biến đổi sau, phép biến đổi nào là phép biến đổi tương đương?

Câu 27: Nghiệm của phương trình \(\frac{{x + 2}}{x} = \frac{{2x + 3}}{{2x - 4}}\) là giá trị nào dưới đây?

Câu 28: Tìm tất cả các giá trị của m để phương trình \({m^2}\left( {x + m} \right) = x + m\) có vô số nghiệm?

Câu 29: Cho phương trình \(\frac{1}{4}{x^2} - \left( {m - 3} \right)x + {m^2} - 2m + 7 = 0\).Tìm m để phương trình có hai nghiệm phân biệt.

Câu 30: Cho phương trình \({x^2} - 2(m - 1)x + {m^2} - 3m + 4 = 0\).Tìm m để phương trình có 2 nghiệm phân biệt \({x_1},{x_2}\) thỏa \(x_1^2 + x_2^2 = 20\).

Câu 31: Biết \(\cos \alpha = \frac{1}{3}\). Giá trị đúng của biểu thức \(P = {\sin ^2}\alpha + 3{\cos ^2}\alpha \) bằng bao nhiêu?

Câu 32: Cho \(\alpha \) là góc tù. Điều khẳng định nào sau đây là đúng?

Câu 33: Cho hình chữ nhật ABCD có \(AB = \sqrt 2 ,\) AD = 1. Tính góc giữa hai vec tơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} .\)

Câu 34: Cho đoạn thẳng AB = 4, AC = 3, \(\overrightarrow {AB} .\overrightarrow {AC} = k\). Hỏi có mấy điểm C để k = -12?

Câu 35: Cho tam giác ABC có H là trực tâm. Biểu thức \({\left( {\overrightarrow {AB} + \overrightarrow {HC} } \right)^2}\) bằng biểu thức nào sau đây?

Câu 36: Nếu tam giác ABC là tam giác đều thì mệnh đề nào sau đây đúng ?

Câu 37: Cho 2 vectơ \(\overrightarrow u = (4;5)\) và \(\overrightarrow v = (3;a)\). Tính a để \(\overrightarrow u .\overrightarrow v = 0\).

Câu 38: Trong mặt phẳng \(\left( {O,\overrightarrow i ,\overrightarrow j } \right)\) cho ba điểm \(A\left( {3;6} \right),{\rm{ }}B\left( {x; - 2} \right),{\rm{ }}C\left( {2;y} \right).\theta \). Tính \(\overrightarrow {OA} .\overrightarrow {BC} .\)

Câu 39: Cho các vectơ \(\vec a = \left( {1; - 2} \right)\), \(\vec b = \left( { - 2; - 6} \right)\). Khi đó góc giữa chúng là bao nhiêu?

Câu 40: Cho hai điểm M(1;-2) và N(-3;4). Khoảng cách giữa hai điểm M và N bằng bao nhiêu?