Đề thi HK1 môn Toán 10 năm 2020 trường THPT Thủ Khoa Huân

Câu hỏi Trắc nghiệm (40 câu):

• Câu 1:

  Mã câu hỏi: 883

  Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng?

  • A.Nếu a và b cùng chia hết cho c thì a + b chia hết cho c.
  • B.Nếu hai tam giác bằng nhau thì diện tích bằng nhau.
  • C.Nếu a chia hết cho 3 thì a chia hết cho 9.
  • D.Nếu một số tận cùng bằng 0 thì số đó chia hết cho 5.

• Câu 2:

  Mã câu hỏi: 885

  Trong các mệnh đề sau, mệnh đề nào không phải là định lí?

  • A.\(\exists x \in N,{\rm{ }}{x^2}\) chia hết cho 3 ⇒ x chia hết cho 3.
  • B.\(\exists x \in N,{\rm{ }}{x^2}\) chia hết cho 6 ⇒ x chia hết cho 3.
  • C.\(\forall x \in N ,{\rm{ }}{x^2}\) chia hết cho 9 ⇒ x chia hết cho 9.
  • D.\(\exists x \in N,{\rm{ }}x\) chia hết cho 4 và 6 ⇒ x chia hết cho 12

• Câu 3:

  Mã câu hỏi: 888

  Trong các tập hợp sau, tập nào là tập rỗng?

  • A.\({T_1} = \left\{ {x \in N|{x^2} + 3x - 4 = 0} \right\}\)
  • B.\({T_1} = \left\{ {x \in N |{x^2} - 3 = 0} \right\}\)
  • C.\({T_1} = \left\{ {x \in N|{x^2} = 2} \right\}\)
  • D.\({T_1} = \left\{ {x \in Q|\left( {{x^2} + 1} \right)\left( {2x - 5} \right) = 0} \right\}\)

• Câu 4:

  Mã câu hỏi: 890

  Cho các tập hợp \(A = \left\{ {x \in R|\,x < 3} \right\}\), \(B = \left\{ {x \in R|1 < x \le 5} \right\}\), \(C = \left\{ {x \in R| - 2 \le x \le 4} \right\}\). Tính \(\left( {B \cup C} \right)\backslash \left( {A \cap C} \right).\)

  • A.[-2; 3)
  • B.[3; 5]
  • C.\(\left( { - \infty ;\,1} \right]\)
  • D.[-2; 5]

• Câu 5:

  Mã câu hỏi: 892

  Cho \(A = \left( { - \infty ;2} \right]\), \(B = \left[ {2; + \infty } \right)\), \(C = \left( {0;3} \right)\). Chọn phát biểu sai.

  • A.\(A \cap C = \left( {0;2} \right]\)
  • B.\(B \cup C = \left( {0; + \infty } \right)\)
  • C.\(A \cup B = R\backslash \left\{ 2 \right\}\)
  • D.\(B \cap C = \left[ {2;3} \right)\)

• Câu 6:

  Mã câu hỏi: 894

  Cho số thực a < 0. Tìm điều kiện cần và đủ để \(\left( { - \infty ;9a} \right) \cap \left( {\frac{4}{a}; + \infty } \right) \ne \emptyset \).

  • A.\( - \frac{2}{3} < a < 0\)
  • B.\( - \frac{3}{4} < a < 0\)
  • C.\( - \frac{2}{3} \le a < 0\)
  • D.\(- \frac{3}{4} \le a < 0\)

• Câu 7:

  Mã câu hỏi: 899

  Tập hợp nào dưới đây là giao của hai tập hợp \(A = \left\{ {x \in : - 1 \le x < 3} \right\}\), \(B = \left\{ {x \in R:\left| x \right| < 2} \right\}\)?

  • A.(-1; 2)
  • B.[0; 2)
  • C.(-2; 3)
  • D.[-1; 2)

• Câu 8:

  Mã câu hỏi: 902

  Cho \(A = \left[ {1; + \infty } \right)\), \(B = \left\{ {x \in R|{x^2} + 1 = 0} \right\}\), \(C = \left( {0;4} \right)\). Tập \(\left( {A \cup B} \right) \cap C\) có bao nhiêu phần tử là số nguyên.

  • A.3
  • B.1
  • C.0
  • D.2

• Câu 9:

  Mã câu hỏi: 907

  Phương trình \(\left| {3x - 1} \right| = 2x - 5\) có bao nhiêu nghiệm?

  • A.Vô số
  • B.1
  • C.0
  • D.2

• Câu 10:

  Mã câu hỏi: 911

  Cho tam giác ABC có G là trọng tâm. Mệnh đề nào sau đây sai?

  • A.\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \) với mọi điểm M
  • B.\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
  • C.\(\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GA} \)
  • D.\(3\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {AC} \)

• Câu 11:

  Mã câu hỏi: 914

  Trong mặt phẳng Oxy, cho \(A\left( {2; - 3} \right)\), \(B\left( {3;4} \right)\). Tìm tọa độ điểm M nằm trên trục hoành sao cho A, B, M thẳng hàng.

  • A.M(1;0)
  • B.M(4;0)
  • C.\(M\left( { - \frac{5}{3}; - \frac{1}{3}} \right)\)
  • D.\(M\left( {\frac{{17}}{7};0} \right)\)

• Câu 12:

  Mã câu hỏi: 918

  Theo thống kê, dân số Việt Nam năm 2016 được ghi lại như sau \(\overline S = 94\,\,444\,\,200 \pm 3000\) (người). Số quy tròn của số gần đúng \(94\,\,444\,\,200\) bằng bao nhiêu?

  • A.94 440 000
  • B.94 450 000
  • C.94 444 000
  • D.94 400 000

• Câu 13:

  Mã câu hỏi: 922

  Tìm TXĐ của hàm số \(y = \sqrt {2 - x} + \sqrt {7 + x} \).

  • A.(-7; 2)
  • B.\(\left[ {2; + \infty } \right)\)
  • C.\(\left[ { - 7;2} \right]\)
  • D.\(R\backslash \left\{ { - 7;2} \right\}\)

• Câu 14:

  Mã câu hỏi: 925

  Tập xác định của hàm số \(y = \left\{ \begin{array}{l} \sqrt {3 - x} \,\,,\,\,x \in \left( { - \infty ;0} \right)\\ \sqrt {\frac{1}{x}} \,\,\,\,\,\,\,\,,\,\,x \in \left( {0; + \infty } \right) \end{array} \right.\) là tập nào dưới đây?

  • A.R \ {0}
  • B.R \ [0; 3]
  • C.R \ {0; 3}
  • D.R

• Câu 15:

  Mã câu hỏi: 931

  Trong các hàm số sau đây: y = |x|; \(y = {x^2} + 4x\); \(y = - {x^4} + 2{x^2}\) có bao nhiêu hàm số chẵn?

  • A.0
  • B.1
  • C.2
  • D.3

• Câu 16:

  Mã câu hỏi: 935

  Cho hàm số y = x - 2. Khẳng định nào sau đây là khẳng định sai?

  • A.Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2.
  • B.Hàm số nghịch biến trên tập R.
  • C.Hàm số có tập xác định là R.
  • D.Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -2.

• Câu 17:

  Mã câu hỏi: 942

  Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l} {x^2} + 3x{\rm{\ khi \ }}x \ge 0\\ 1 - x{\rm{\ khi \ }}x < 0 \end{array} \right.\). Khi đó, \(f\left( 1 \right) + f\left( { - 1} \right)\) bằng bao nhiêu?

  • A.2
  • B.-3
  • C.6
  • D.0

• Câu 18:

  Mã câu hỏi: 945

  Một hàm số bậc nhất y = f(x) có \(f\left( { - 1} \right) = 2,f\left( 2 \right) = - 3\). Hỏi hàm số đó là hàm số nào dưới đây?

  • A.\(y = - 2x + 3\)
  • B.\(y = \frac{{ - 5x - 1}}{3}\)
  • C.\(y = \frac{{ - 5x + 1}}{3}\)
  • D.\(y = 2x - 3\)

• Câu 19:

  Mã câu hỏi: 950

  Với những giá trị nào của m thì hàm số \(f\left( x \right) = \left( {m + 1} \right)x + 2\) đồng biến?

  • A.m = 0
  • B.m = 1
  • C.m < 0
  • D.\(m > - 1\)

• Câu 20:

  Mã câu hỏi: 955

  Cho hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) lần lượt có phương trình: \(mx + \left( {m - 1} \right)y - 2\left( {m + 2} \right) = 0\) và \(3mx - \left( {3m + 1} \right)y - 5m - 4 = 0\). Xác định vị trí tương đối của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) khi \(m = \frac{1}{3}\).

  • A.Song song với nhau.
  • B.Cắt nhau tại 1 điểm.
  • C.Vuông góc nhau.
  • D.Trùng nhau.

• Câu 21:

  Mã câu hỏi: 959

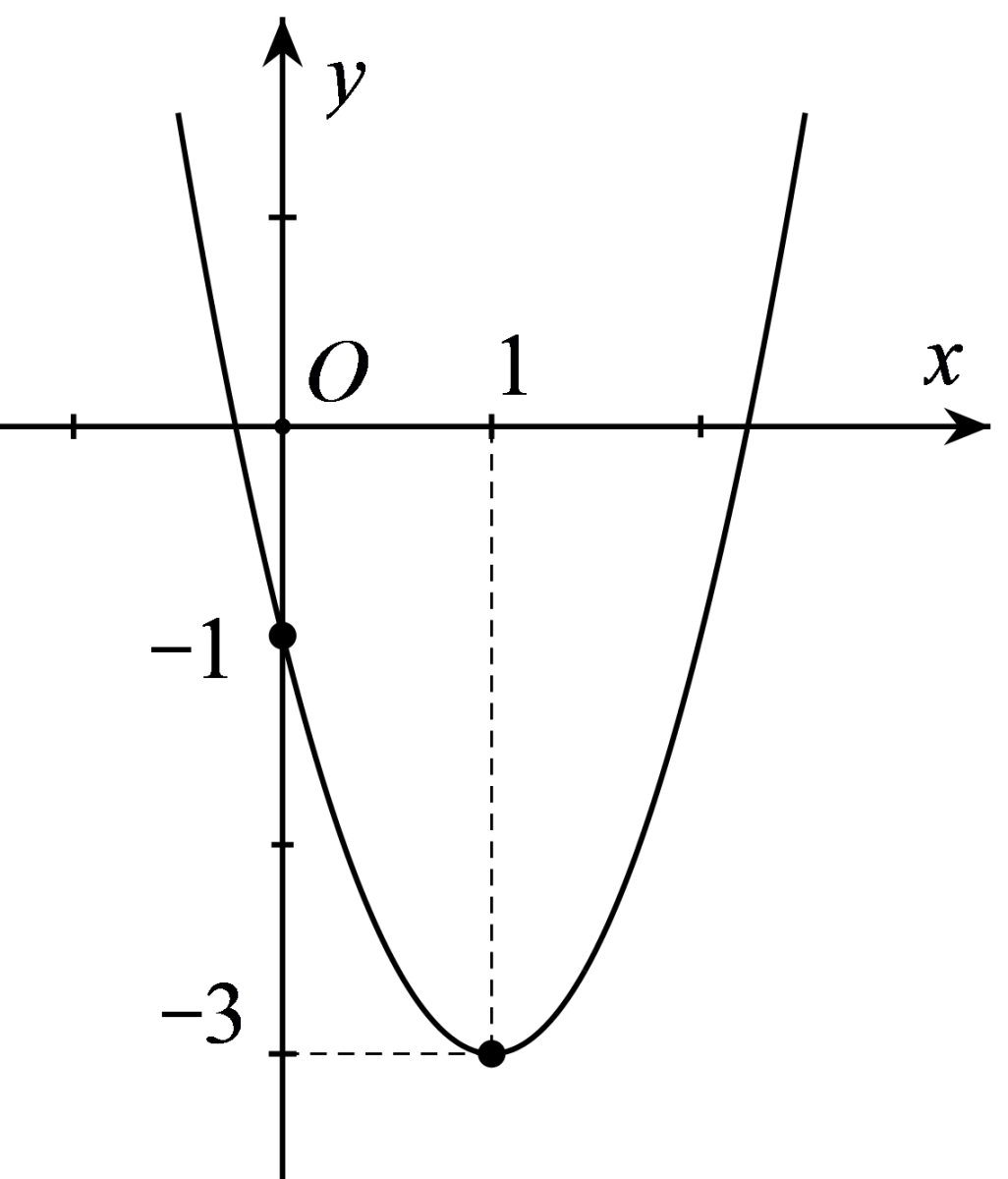
  Cho parabol \(\left( P \right):y = a{x^2} + bx + c\) có đồ thị như hình bên. Phương trình của parabol này là phương trình nào dưới đây?

  

  • A.\(y = 2{x^2} - 4x - 1\)
  • B.\(y = 2{x^2} + 3x - 1\)
  • C.\(y = 2{x^2} + 8x - 1\)
  • D.\(y = 2{x^2} - x - 1\)

• Câu 22:

  Mã câu hỏi: 964

  Hàm số nào sau đây có giá trị nhỏ nhất tại \(x = \frac{3}{4}\)?

  • A.\(y = 4{x^2} - 3x + 1\)
  • B.\(y = - {x^2} + \frac{3}{2}x + 1\)
  • C.\(y = - 2{x^2} + 3x + 1\)
  • D.\(y = {x^2} - \frac{3}{2}x + 1\)

• Câu 23:

  Mã câu hỏi: 968

  Parabol \(y = a{x^2} + bx + 2\) đi qua hai điểm M(1; 5) và N(-2; 8) có phương trình là phương trình nào dưới đây?

  • A.\(y = {x^2} + x + 2\)
  • B.\(y = {x^2} + 2x\)
  • C.\(y = 2{x^2} + x + 2\)
  • D.\(y = 2{x^2} + 2x + 2\)

• Câu 24:

  Mã câu hỏi: 972

  Parabol \(y = a{x^2} + bx + c\) đi qua A(8;0) và có đỉnh S(6;-12) có phương trình là phương trình nào dưới đây?

  • A.\(y = {x^2} - 12x + 96\)
  • B.\(y = 2{x^2} - 24x + 96\)
  • C.\(y = 2{x^2} - 36x + 96\)
  • D.\(y = 3{x^2} - 36x + 96.\)

• Câu 25:

  Mã câu hỏi: 975

  Tìm giao điểm của parabol \(y = {x^2} - 3{\rm{x}} + 2\) với đường thẳng \(y = x - 1\).

  • A.\(\left( {1;0} \right),{\rm{ }}\left( {3;2} \right).\)
  • B.\(\left( {0; - 1} \right),\left( { - 2; - 3} \right).\)
  • C.(-1; 2); (2;1)
  • D.(2; 1); (0; -1)

• Câu 26:

  Mã câu hỏi: 979

  Trong bốn phép biến đổi sau, phép biến đổi nào là phép biến đổi tương đương?

  • A.\(\frac{{x\left( {x - 1} \right)}}{{x - 1}} = 1 \Leftrightarrow x = 1\)
  • B.\(\left| x \right| = 2 \Leftrightarrow x = 2\)
  • C.\(x + \sqrt {x - 4} = 3 + \sqrt {x - 4} \Leftrightarrow x = 3\)
  • D.\(x - \sqrt {x - 5} = 3 \Leftrightarrow x - 3 = \sqrt {x - 5} \)

• Câu 27:

  Mã câu hỏi: 983

  Nghiệm của phương trình \(\frac{{x + 2}}{x} = \frac{{2x + 3}}{{2x - 4}}\) là giá trị nào dưới đây?

  • A.\(x = - \frac{3}{8}\)
  • B.\(x = \frac{3}{8}\)
  • C.\(x = \frac{8}{3}\)
  • D.\(x = - \frac{8}{3}\)

• Câu 28:

  Mã câu hỏi: 987

  Tìm tất cả các giá trị của m để phương trình \({m^2}\left( {x + m} \right) = x + m\) có vô số nghiệm?

  • A.\(m = \pm1\)
  • B.m = 0 hoặc m = 1
  • C.m = 0 hoặc m = -1
  • D.\( - 1 < m < 1,\,m \ne 0\)

• Câu 29:

  Mã câu hỏi: 991

  Cho phương trình \(\frac{1}{4}{x^2} - \left( {m - 3} \right)x + {m^2} - 2m + 7 = 0\).Tìm m để phương trình có hai nghiệm phân biệt.

  • A.\(m \ge \frac{1}{2}\)
  • B.\(m < - \frac{1}{2}\)
  • C.\(m > \frac{1}{2}\)
  • D.\(m < \frac{1}{2}\)

• Câu 30:

  Mã câu hỏi: 995

  Cho phương trình \({x^2} - 2(m - 1)x + {m^2} - 3m + 4 = 0\).Tìm m để phương trình có 2 nghiệm phân biệt \({x_1},{x_2}\) thỏa \(x_1^2 + x_2^2 = 20\).

  • A.\(m = - 3,m = 4\)
  • B.m = 4
  • C.m = -3
  • D.\(m = 3,m = - 4\)

• Câu 31:

  Mã câu hỏi: 999

  Biết \(\cos \alpha = \frac{1}{3}\). Giá trị đúng của biểu thức \(P = {\sin ^2}\alpha + 3{\cos ^2}\alpha \) bằng bao nhiêu?

  • A.\(\dfrac13\)
  • B.\(\dfrac{{10}}{9}\)
  • C.\(\dfrac{{11}}{9}\)
  • D.\(\dfrac{{4}}{3}\)

• Câu 32:

  Mã câu hỏi: 1003

  Cho \(\alpha \) là góc tù. Điều khẳng định nào sau đây là đúng?

  • A.\(\sin \alpha < 0\)
  • B.\(\cos \alpha > 0\)
  • C.\(\tan \alpha < 0\)
  • D.\(\cot \alpha > 0\)

• Câu 33:

  Mã câu hỏi: 1007

  Cho hình chữ nhật ABCD có \(AB = \sqrt 2 ,\) AD = 1. Tính góc giữa hai vec tơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} .\)

  • A.89^o
  • B.92^o
  • C.109^o
  • D.91^o

• Câu 34:

  Mã câu hỏi: 1009

  Cho đoạn thẳng AB = 4, AC = 3, \(\overrightarrow {AB} .\overrightarrow {AC} = k\). Hỏi có mấy điểm C để k = -12?

  • A.2
  • B.0
  • C.1
  • D.3

• Câu 35:

  Mã câu hỏi: 1012

  Cho tam giác ABC có H là trực tâm. Biểu thức \({\left( {\overrightarrow {AB} + \overrightarrow {HC} } \right)^2}\) bằng biểu thức nào sau đây?

  • A.\(A{B^2} + H{C^2}\)
  • B.\({\left( {AB + HC} \right)^2}\)
  • C.\(A{C^2} + A{H^2}\)
  • D.\(A{C^2} + 2A{H^2}.\)

• Câu 36:

  Mã câu hỏi: 1015

  Nếu tam giác ABC là tam giác đều thì mệnh đề nào sau đây đúng ?

  • A.\(\overrightarrow {AB.} \overrightarrow {AC} = \frac{1}{2}A{B^2}\)
  • B.\(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{\sqrt 3 }}{2}A{B^2}\)
  • C.\(\overrightarrow {AB.} \overrightarrow {AC} = \frac{1}{4}A{B^2}\)
  • D.\(\overrightarrow {AB.} \overrightarrow {AC} = 0.\)

• Câu 37:

  Mã câu hỏi: 1018

  Cho 2 vectơ \(\overrightarrow u = (4;5)\) và \(\overrightarrow v = (3;a)\). Tính a để \(\overrightarrow u .\overrightarrow v = 0\).

  • A.\(a = \frac{{12}}{5}\)
  • B.\(a =- \frac{{12}}{5}\)
  • C.\(a = \frac{5}{{12}}\)
  • D.\(a =- \frac{5}{{12}}\)

• Câu 38:

  Mã câu hỏi: 1022

  Trong mặt phẳng \(\left( {O,\overrightarrow i ,\overrightarrow j } \right)\) cho ba điểm \(A\left( {3;6} \right),{\rm{ }}B\left( {x; - 2} \right),{\rm{ }}C\left( {2;y} \right).\theta \). Tính \(\overrightarrow {OA} .\overrightarrow {BC} .\)

  • A.\(\overrightarrow {OA} .\overrightarrow {BC} = 3x + 6y - 12\)
  • B.\(\overrightarrow {OA} .\overrightarrow {BC} = - 3x + 6y + 18\)
  • C.\(\overrightarrow {OA} .\overrightarrow {BC} = - 3x + 6y + 12\)
  • D.\(\overrightarrow {OA} .\overrightarrow {BC} = 0\)

• Câu 39:

  Mã câu hỏi: 1025

  Cho các vectơ \(\vec a = \left( {1; - 2} \right)\), \(\vec b = \left( { - 2; - 6} \right)\). Khi đó góc giữa chúng là bao nhiêu?

  • A.45^o
  • B.60^o
  • C.30^o
  • D.135^o

• Câu 40:

  Mã câu hỏi: 1028

  Cho hai điểm M(1;-2) và N(-3;4). Khoảng cách giữa hai điểm M và N bằng bao nhiêu?

  • A.4
  • B.6
  • C.\(3\sqrt 6 \)
  • D.\(2\sqrt {13} \)