Giải Toán 10 SGK nâng cao Chương 6 Luyện tập (trang 191, 192)

Cho ngũ giác đều A₀A₁A₂A₃A₄ nội tiếp đường tròn tâm O (các đỉnh được sắp xếp theo chiều ngược chiều quay của kim đồng hồ). Tính số đo (độ và radian) các cung $A_0{A}_i,A_i{A}_j$

Hướng dẫn giải:

Sđ cung $A_0{A}_i=i\frac{2\pi }{5}+k2\pi$ hay sđ cung $A_0{A}_i=i{.72}^0+k{360}^0,k\in Z,\mathrm{\forall }i=\overline{0,4}$

Theo hệ thức Salo, ta có:

Sđ cung A_iA_j = sđ cung A₀A_j -  sđ cung A₀A_i + $k2\pi \left(k\in Z\right)$ $=\frac{\left(j-i\right).2\pi }{5}+k2\pi \left(i,j=\overline{0,4};i\ne j,k\in Z\right)$

hay $\left(j-i\right){.72}^0+k{360}^0$ $\left(i,j=\overline{0,4};i\ne j,k\in Z\right)$

Tìm góc lượng giác (Ou, Ov) có số đo dương nhỏ nhất, biết một góc lượng giác (Ou, Ov) có số đo:

a) - 90⁰

b) 1000⁰

c) $\frac{30\pi }{7}$

d) $-\frac{15\pi }{11}$

Hướng dẫn giải:

Nếu góc lượng giác có số đo là a⁰ thì ta cần xác định số nguyên k để : 0^o < a⁰ + k360⁰ ≤ 360⁰. Khi đó: a⁰ + k360⁰  là số đo dương nhỏ nhất cần tìm.

Câu a:

Với a = - 90⁰ thì k = 1. Số đo dương nhỏ nhất cần tìm là 270⁰

Câu b:

Với a = 1000⁰ thì k = - 2. Số đo dương nhỏ nhất cần tìm là 280⁰

Câu c:

Với $\alpha =\frac{30\pi }{7}$ thì k = - 2. Số đo dương nhỏ nhất cần tìm là: $\frac{2\pi }{7}$

Câu d:

Với $\alpha =-\frac{15\pi }{11}$ thì k = 1. Số đo dương nhỏ nhất cần tìm là: $\frac{7\pi }{11}$

Tìm số đo radian α, - π < α ≤ π, của góc lượng giác có cùng tia đầu, tia cuối với góc trên mỗi hình sau.

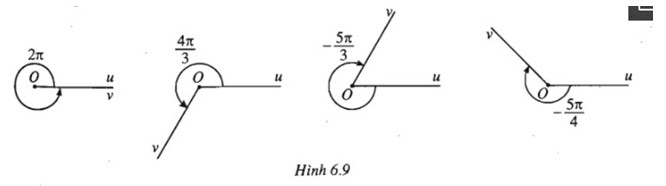
Hướng dẫn giải:

a) $\alpha =0$

b) $\alpha =\frac{4\pi }{3}-2\pi =-\frac{2\pi }{3}$

c) $\alpha =2\pi -\frac{5\pi }{3}=\frac{\pi }{3}$

d) $\alpha =2\pi -\frac{5\pi }{4}=\frac{3\pi }{4}$

Chứng minh rằng hai tia Ou và Ov vuông góc với nhau khi và chỉ khi góc lượng giác (Ou; Ov) có số đo là $\left(2k+1\right).\frac{\pi }{2},k\in Z$

Hướng dẫn giải:

Ta có:

$\begin{array}{l}Ou\mathrm{\perp }Ov\iff [\begin{array}{c}sd\left(Ou,Ov\right)=\frac{\pi }{2}+k2\pi \left(k\in Z\right)\\ sd\left(Ou,Ov\right)=-\frac{\pi }{2}+l2\pi \left(l\in Z\right)=\frac{\pi }{2}+\left(2l-1\right)\pi \end{array}\\ \iff sd\left(Ou,Ov\right)=\frac{\pi }{2}+m\pi =\frac{\pi }{2}\left(1+2m\right)\left(m\in Z\right)\end{array}$ 

Kim giờ và kim phút đồng hồ bắt đầu cùng chạy từ vị trí Ox chỉ số 12 (tức lúc 0 giờ). Sau thời gian t giờ (t ≥ 0), kim giờ đến vị trí tia Ou kim phút đến vị trí tia Ov.

a) Chứng minh rằng khi quay như thế, kim giờ quét góc lượng giác (Ox; Ou) có số đo $-\frac{\pi }{6}t$, kim phút quét góc lượng giác (Ox; Ov) có số đo: - 2πt. Hãy tìm số đo của góc lượng giác (Ou; Ov) theo t.

b) Chứng minh rằng hai tia Ou, Ov trùng nhau khi và chỉ khi $t=\frac{12k}{11}$ với k là một số tự nhiên nào đó.

c) Chứng minh rằng trong 12 giờ (0 ≤ t ≤ 12), hai tia Ou’ và Ov’ ở vị trí đối nhau khi và chỉ khi $t=\frac{6}{11}\left(2k+1\right)$ với k = 0, 1, ...10    

Hướng dẫn giải:

Câu a:

Trong một giờ, góc lượng giác có số đo $-\frac{2\pi }{12}$, nên trong t giờ, kim phút quét góc lượng giác (Ox, Ov) có số đo -2πt, kim giờ quét góc (Ox, Ou) có số đo $-\frac{\pi }{6}t$.

Từ đó, theo hệ thức Salo, góc lượng giác (Ou, Ov) có:

sđ(Ou, Ov) = sđ(Ox, Ov) - sđ(Ox, Ou) + 12π = $-2\pi t+\frac{\pi }{6}t+12\pi =\left(-\frac{11}{6}t+2l\right)\pi \left(l\in Z\right)$

Câu b:

Hai tia Ou, Ov trùng nhau khi và chỉ khi (Ou, Ov) = 2mπ (m ∈ Z)
Suy ra $-\frac{11}{6}t+2l=2m$, tức là $\frac{11}{6}t=2\left(l-m\right)$

Do đó $t=\frac{12k}{11},k\in Z$

Vì $t\ge 0$ nên $k\in N$

Câu c:

Hai tia Ou, Ov đối nhau khi và chỉ khi (Ou, Ov) = (2m – 1)π (m ∈ Z)

Suy ra $-\frac{11t}{6}+2l=2m-1$, tức là $\frac{11t}{6}=2\left(l-m\right)+1$

Do đó $t=\frac{6}{11}\left(2k+1\right)\pi \left(k\in Z\right)$

Vì $0\le t\le 12$ nên k = 0, 1, 2,...,10

Hỏi hai góc lượng giác có số đo $\frac{35\pi }{3}$ và $\frac{m\pi }{5}$ (m ∈ Z) có thể có cùng tia đầu tia cuối không.

Hướng dẫn giải:

Ta có: $\frac{35\pi }{3}=-\frac{\pi }{3}+12\pi$ như vậy không thể tồn tại m ∈ Z nào để góc lượng giác trên có cùng tia đầu và tia cuối.

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 6 Luyện tập (trang 191, 192) với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Chúng tôi hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.