Bài tập SGK Bài 1: Hàm số

Bài tập 1 trang 38 SGK Đại số 10

Tìm tập xác định của các hàm số sau:

a) $y=\frac{3x-2}{2x+1};$

b) $y=\frac{x-1}{x^2+2x-3};$

c) $y=\sqrt{2x+1}-\sqrt{3-x}.$

Bài tập 2 trang 38 SGK Đại số 10

 Cho hàm số $y=\{\begin{array}{l}x+1,x\ge 2\\ x^2-2,x<2\end{array}$

Tính giá trị của hàm số tại $x=3,x=-1,x=2$.

Bài tập 3 trang 38 SGK Đại số 10

Cho hàm số $y=3x^2-2x+1$. Các điểm sau có thuộc đồ thị hay không?

a) M (- 1;6);

b) N (1;1);

c) P(0;1).

Bài tập 4 trang 39 SGK Đại số 10

Xét tính chẵn lẻ của hàm số: 

a) $y=|x|$;

b) $y=(x+2{)}^2$     

c) $y=x^3+x$ ;

d) $y=x^2+x+1$.

Bài tập 2.1 trang 29 SBT Toán 10

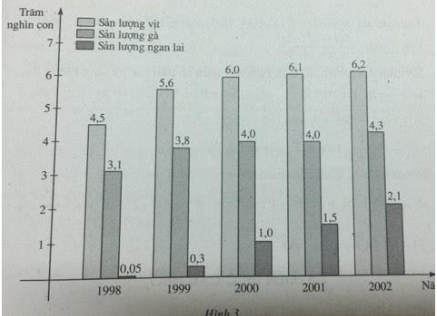
Biểu đồ sau (h.3) biểu thị sản lượng vịt, gà và ngan lai qua 5 năm của một trang trại. Coi y = f(x), y = g(x) và y = h(x) tương ứng là các hàm số biểu thị sự phụ thuộc số vịt, số gà và số ngan lai vào thời gian xx. Qua biểu đồ, hãy:

a) Tìm tập xác định của mỗi hàm số đã nêu.

b) Tìm các giá trị f(2002),g(1999), h(2000)và nêu ý nghĩa của chúng;

c) Tìm hiệu h(2002) – h(1999) và nêu ý nghĩa của nó.

Bài tập 2.2 trang 29 SBT Toán 10

Tìm tập xác định của các hàm số

a) $y=-x^5+7x-2$

b) $y=\frac{3x+2}{x-4}$

c) $y=\sqrt{4x+1}-\sqrt{-2x+1}$

d) $y=\frac{2x+1}{\left(2x+1\right)\left(x-3\right)}$

Bài tập 2.3 trang 30 SBT Toán 10

Cho hàm số

$y=f\left(x\right)=\{\begin{array}{l}\frac{2x-3}{x-1},x\le 0\\ -x^2+2x,x>0\end{array}$

Tính giá trị của hàm số đó tại x = 5; x = −2; x = 0; x = 2.

Bài tập 2.4 trang 30 SBT Toán 10

Cho các hàm số :

$\begin{array}{l}f\left(x\right)=x^2+2+\sqrt{2-x};g\left(x\right)=-2x^2-3x+5;\\ u\left(x\right)=\{\begin{array}{c}\sqrt{3-x},x<2\\ \sqrt{x^2-4},x\ge 2\end{array};v\left(x\right)=\{\begin{array}{c}\sqrt{6-x},x\le 0\\ x^2+1,x>0\end{array}\end{array}$

Tính các giá trị $f\left(-2\right)-f\left(1\right);g\left(3\right);f\left(-7\right)-g\left(-7\right)$

$f\left(-1\right)-u\left(-1\right);u\left(3\right)-v\left(3\right);v\left(0\right)-g\left(0\right);\frac{f\left(2\right)-f\left(-2\right)}{v\left(2\right)-v\left(-3\right)}$

Bài tập 2.5 trang 31 SBT Toán 10

Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng

a) y = −2x+3 trên R.

b) y = x²+10x+9 trên (−5;+∞);

c) $y=-\frac{1}{x+1}$ trên (−3;−2) và (2;3).

Bài tập 2.6 trang 31 SBT Toán 10

Xét tính chẵn, lẻ của các hàm số

a) y = −2 ;

b) y = 3x²−1 ;  

c) y = −x⁴+3x−2.

d) $y=\frac{-x^4+x^2+1}{x}$.

Bài tập 2.7 trang 31 SBT Toán 10

Tập xác định của hàm số $y=\frac{3x+10}{x^2+14x+45}$ là

A. R

B. R\{-5;9}

C. R\{-5;- 9}

D. R\{5;9}

Bài tập 2.8 trang 31 SBT Toán 10

Hàm số $y=\sqrt{x+7}+\frac{2}{x^2+6x-16}$ có tập xác định D bằng

A. (7;+∞)

B. (7;+∞)∖{−8;2}

C. [−7;7]∖{2}

D. [−7;+∞)∖{2}